使用微軟的D3D來編程需要熟悉3D幾何原理���。本節(jié)介紹建立3D世界的最重要的幾何概念�����。
1.1.1. 3-D坐標(biāo)系統(tǒng)
典型的3D圖形程序使用兩種笛卡兒坐標(biāo)系統(tǒng):左手和右手���。兩個坐標(biāo)系統(tǒng)中���,正X軸指向右邊�����,正Y軸指向上�。你可以通過你左右手指間指向與正X軸相同時大拇指指向的方向來記住坐標(biāo)方向。下圖描述了這兩種系統(tǒng)���。
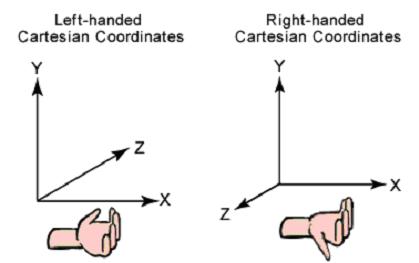
微軟的D3D使用左手系統(tǒng),如果你正在將一個基于右手坐標(biāo)系統(tǒng)的程序?qū)氲匠绦蛑?��,你必須做兩個改變過度到D3D。
1.1.2. 3-D原基(點陣)
一個3D原基就是一個形成單個3D實體的頂點集合�����。最簡單的原基是3D系統(tǒng)中點的集合���,也叫做點列表���。
當(dāng)然�����,3D原基是多邊形�����。一個多邊形是一個至少包括3個頂點的封閉的圖形。最簡單的多邊形是3角形。微軟D3D使用三角形來組成大多數(shù)的多邊形���,因為三角形中的三個頂點是共面的,渲染不是平面的頂點是無效的。你可以通過合并三角形來形成大的���、復(fù)雜的多邊形和網(wǎng)格。
下圖描述了一個立方體���。正方體的每個面由2個三角形組成,所有三角形形成一個正方體原始���。你能使用材質(zhì)和原料到原始的每個面上來使他們看起來象一個固體形狀�����。

你也可以用三角形來建立表面平滑的平面�����。下面的圖顯示了一個使用三角形來仿真的球體�����;在應(yīng)用材料以后,在渲染的時候球體看起來平滑很多。如果你使用Gouraud陰影�,更是這樣���。詳細(xì)的細(xì)節(jié)參見Gouraud 陰影���。
1.1.3. 面和頂點法線向量
網(wǎng)格中的每個面都有一個正交的法線向量�����。向量的方向是由頂點定義的順序和左右手坐標(biāo)系統(tǒng)。正面法線從正面的前邊指出。微軟的D3D系統(tǒng)�,僅僅正面的前邊是可見的�����,前面就是頂點以順時針方向定義的面。
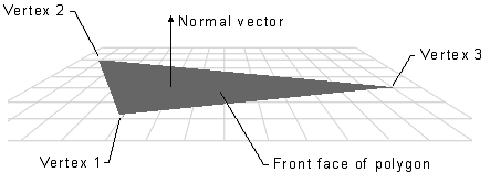
D3D使用頂點法線來表示陰影、光線和材質(zhì)效果。
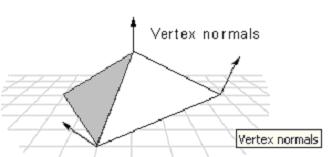
在一個多邊形上應(yīng)用陰影時�,D3D使用頂點法線來計算光源和表面之間的角度�����。其為頂點計算色彩和亮度值�����,并且通過所有原始表面來為每個頂點加入�。D3D通過角度來計算光亮度值�。角度越大,亮度越小�。
如果你正在一個平面上創(chuàng)建一個對象�����,設(shè)置頂點法線來指向表面的垂線,就如下圖所示�����。定義一個由兩個三角形組成的平面�。
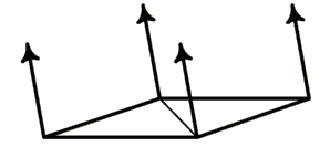
然而,很可能你的對象有一些不共面條的三角形組成�;為了獲得通過所有三角形帶的平滑陰影�,一個簡單的辦法就是首先計算與頂點相關(guān)的每個多邊形曲面法線矢量�。頂點法線被設(shè)置為對于每個曲面法線有相同的角度。但這個方法在復(fù)雜的初基(點陣)并不是特別有效�。
上面的方法通過下圖來描述�����,他展示了兩個曲面,S1和S2有一條邊相交���。S1和S2的法線使用藍(lán)色表示。頂點法線矢量用紅色顯示�。頂點法線矢量和S1和S2面上的曲面法線角度一樣�。當(dāng)這兩個表面被點亮或使用Gouraud陰影���,結(jié)果在他們之間是一個平滑的陰影���,平滑的圓形邊�。
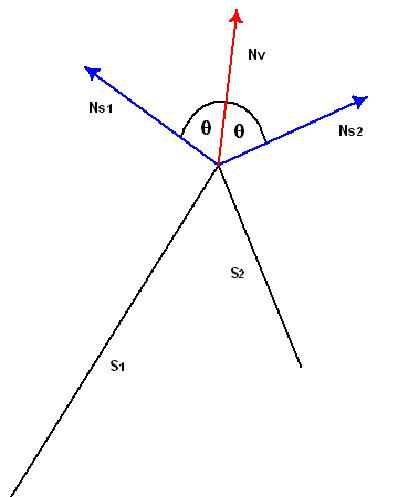
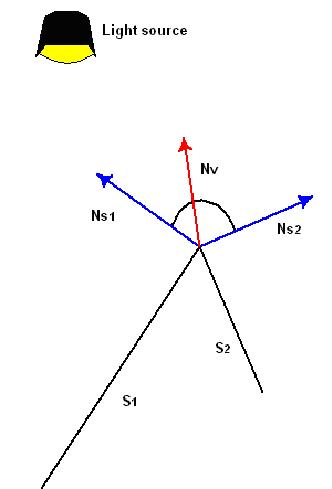
如果頂點發(fā)現(xiàn)朝其中關(guān)聯(lián)的一個面傾斜���,它導(dǎo)致指向表面的光強(qiáng)度增加或降低�,主要依賴于和光源之間的角度。下面表明這個例子���。同樣,這些面是邊相交的,頂點法線向S1傾斜導(dǎo)致其和光源之間角度較小�。
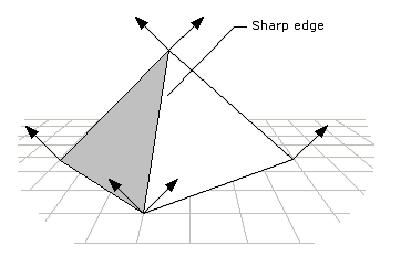
你可以使用Gouraud陰影來在3D場景中顯示一些帶有明顯邊的對象�����,為了這么做�����,需要在每個明顯邊緣的面相交處復(fù)制頂點法線矢量,如下圖顯示:
如果你使用DrawPrimitive方法來粉刷你的場景�,定義帶有明顯邊界的對象作為一個三角形列表而不是三角形帶�。當(dāng)你定義一個作為三角形帶的對象���,D3D將其作為一個由多個三角形面組成的單個多邊形���。Gouraud陰影應(yīng)用到通過多邊形每個面以及相鄰面之間�����;結(jié)果是具有從一個面到另一個面平滑陰影的對象���;因為一個三角形列是一系列分解三角形面組成的一個多邊形���,D3D使用Gouraud陰影貫穿多邊形的每個面;然而,它并不應(yīng)用到面到面,如果兩個或多個三角形列中的三角形相鄰�����,在他們之間會有一個明顯的邊界���。
另外在粉刷一個帶有明顯邊界的對象時選擇是將其作為平面陰影�����。這是最有效的方法���,但他可能導(dǎo)致一個對象沒有使用Gouraud陰影粉刷理想的效果���。
1.1.4. 光柵化規(guī)則
經(jīng)常�,指定的頂點并不正好和屏幕上的像素相匹配���;當(dāng)這個發(fā)生的時候���,D3D使用三角形光柵化原則來那些像素對應(yīng)到給定的三角形上�����。
1. 三角形光柵化原則
2. 點和線規(guī)則
3. 點精靈規(guī)則
1.1.4.1.1. 三角形光柵化規(guī)則
D3D使用頂-左填充約定作為填充幾何算法�。這同微軟GDI以及OpenGL的矩形填充約定相同���。在D3D中�����,像素的中央是決定性點,如果中心在一個三角形中���,那這個像素是三角形的一部分。像素中心是整數(shù)坐標(biāo)���。
這個D3D使用的三角形光柵化原則并不是必須應(yīng)用到所有可用的硬件上;你的測試或許揭示這些規(guī)則小的變化���。
下圖顯示一個左上角在(0,0)點的矩形,其右下角在(5,5)點���;這個舉行填充了25個像素,就像你預(yù)期的一樣�,矩形的寬度定義為右-左�,高度是底減去頂部�����。
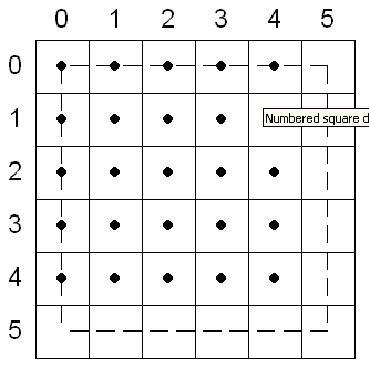
在頂左填充約定中���,頂指的是水平跨度的垂直位置�,左指的是一個像素寬度的水平位置。一個邊不能是頂邊,除非它是水平的;通常大多數(shù)三角形有唯一的左和右邊�。
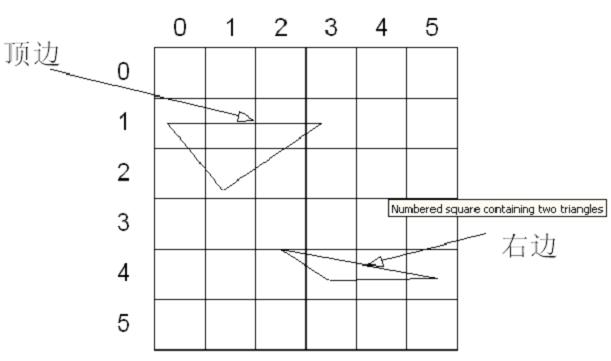
頂-左填充約定決定了當(dāng)一個三角形穿過一個像素中心時D3D的行為���。下圖展示了兩個三角形�,一個是(0�,0),(5,0)�,(5�����,5);而另外一個在(0,5)���,(0�,0),(5���,5)。這個例子中第一個三角形得到15個像素(黑色顯示)�,然而第二個得到10個像素(灰色顯示)�,因為他們共享邊是第一個三角形的左邊邊�����。
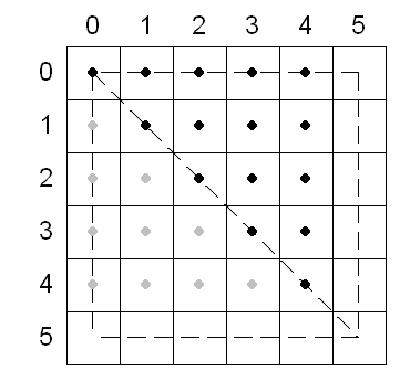
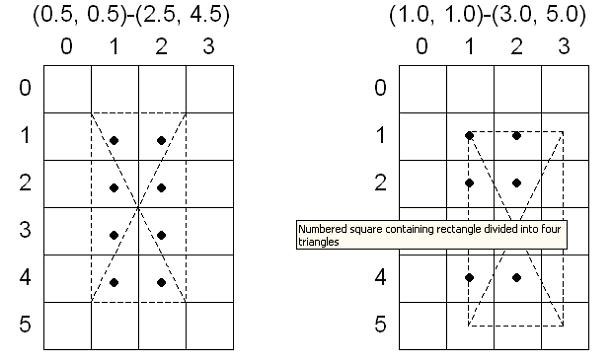
如果你定義一個矩形其左上角在(0.5�����,0.5),右下角在(2.5,4.5)�����,中心點是(1.5�,2.5)。當(dāng)D3D光柵 tesselate這個矩形時�,每個像素的中心都明顯的在矩形的內(nèi)部���,且左上角填充規(guī)則不必要�����。下圖說明這個內(nèi)容;矩形中的像素依據(jù)D3D包括的三角形標(biāo)記�。
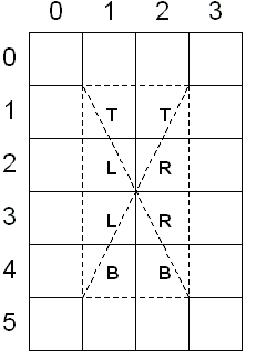
如果你移動上面例子中的矩形使其左上角坐標(biāo)在(1.0,1.0)���,它的右下角在(3.0�����,5.0)�����,它的中心點在(2.0�,3.0)�����,D3D使用左上填充約定�;大多數(shù)三角形在兩個或多個三角形的邊界上�����,如下圖所示:
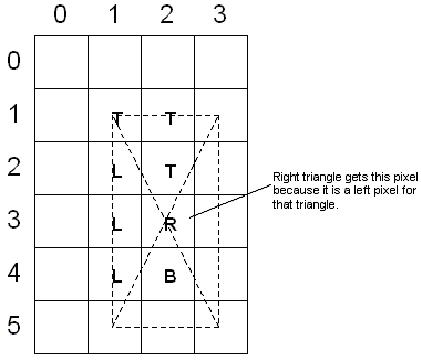
兩個矩形中���,影響的相同像素如下:
1.1.4.1.2. 點和線規(guī)則
點和點精靈粉刷方式是相同的�����,他們都依照屏幕對齊的四邊形方式粉刷���,從而和多邊形粉刷具有相同的規(guī)則�。
Non-antialiased線粉刷方式同GDI相同。
更多關(guān)于antialiased線的粉刷�����,見ID3DXLine�。
1.1.4.1.3. 精靈點規(guī)則
精靈點和補(bǔ)丁初基首先被鑲嵌到三角形中�����,然后使用結(jié)果三角形光柵化原則來處理;更多的信息參見:精靈點。
1.1.5. 矩形
貫穿D3D和Windows編程���,屏幕上的對象都?xì)w諸于范圍矩形。矩形的邊同屏幕的邊平行,因此舉行可以使用兩個點來表示,左上角和右下角。大多數(shù)程序在blitting到屏幕上或執(zhí)行hit檢測的時候使用攜帶矩形信息的RECT結(jié)構(gòu)。
在C++中���,RECT結(jié)構(gòu)定義如下:
typedef struct tagRECT { LONG left; // This is the upper-left corner x-coordinate.
LONG top; // The upper-left corner y-coordinate.
LONG right; // The lower-right corner x-coordinate.
LONG bottom; // The lower-right corner y-coordinate.
} RECT, *PRECT, NEAR *NPRECT, FAR *LPRECT;
前面的例子中,left和top成員指的是矩形左上角的x和y坐標(biāo)�����,同樣right和bottom指的是右下角的x和y的坐標(biāo)�����。下圖描述了你怎么形象化的理解這些值�����。
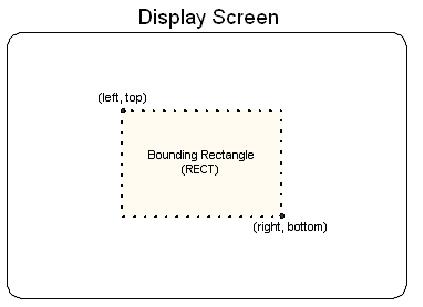
為了效率、一致性和容易使用的目的,所有D3D顯示函數(shù)都使用矩形來工作�。
1.1.6. 三角形Interpolants
在粉刷過程中���,管道插入穿過每個三角形的頂點數(shù)據(jù)���;頂點數(shù)據(jù)可以明顯的變化并包含(但不限制于)彌漫的色彩���、有金屬光澤的色彩���、彌漫的alpha(三角形通明性)���、金屬光澤alpha和霧化因素(為頂點管道降低金屬光澤alpha以及降低可編程頂點管道霧化登記);這個頂點數(shù)據(jù)被定義為頂點聲明�����。
對于許多頂點數(shù)據(jù)來說���,插入獨立于當(dāng)前的陰影模式�����,如下表描述:
|
陰影模式 |
描述 |
|
平面 |
僅僅霧化因素被插入到平面陰影模式中�;對于所有其他的插入�����,第一個頂點的顏色將應(yīng)用為穿過整個面的色彩 |
|
Gouraud |
在所有三個頂點之間執(zhí)行線性插入 |
彌漫色彩和金屬光澤色彩不同對待�,依賴于顏色模式�。在RGB模式中,系統(tǒng)在插入中使用紅�、綠���、藍(lán)成分�。
色彩的Alpha成分作為一個單獨的interpolant對待�,因為設(shè)備驅(qū)動可以用兩種方法來實現(xiàn)通明性:使用材質(zhì)混合或使用點畫法。
使用D3DCAPS9結(jié)構(gòu)體的ShadeCaps成員來決定當(dāng)前設(shè)備驅(qū)動支持什么樣的interpolation形式�����。
1.1.7. 矢量���、頂點和四元數(shù)
貫穿D3D,頂點描述位置和方向�����;初基中的每個點被描述為一個具有位置���、顏色���、材質(zhì)坐標(biāo)和給定方向的法線向量的一個向量�。
四元數(shù)添加一個元素到[x ,y ,z]值中來定義一個三分量矢量�����。四元數(shù)是3D旋轉(zhuǎn)時使用的矩陣方法的另一個選擇���;一個四元數(shù)表達(dá)一個3D平面的軸以及繞軸旋轉(zhuǎn)的度�����。例如:四元數(shù)可能表示一個(1,1,2)軸和一個1弧度的旋轉(zhuǎn)。四元數(shù)攜帶重要的信息�,但他們真正的作用來自兩個你可以執(zhí)行的操作:組合和插入(interpolation)���。
在一個四元數(shù)上執(zhí)行合成操作和合并他們很相似�����,兩個四元數(shù)的合成標(biāo)記為:
Q=q1Oq2
兩個四元數(shù)的合成應(yīng)用到幾何學(xué)上意味著:繞軸2旋轉(zhuǎn)幾何圖形旋度2,然后繞軸1旋轉(zhuǎn)旋度1���;這個例子中,Q表示一個繞一個軸的旋轉(zhuǎn)角度�,也是作用q2然后q1到幾何圖形上的結(jié)果�����。
使用四元數(shù)interpolation,程序可以從一個軸和方向計算到另一個的平滑的和合理的路徑。因此�,在q1和q2之間的interpolation為從嚴(yán)格方向到另一個方向提供了動畫的簡單方法。
當(dāng)你一起使用組合和interpolation時候���,他們?yōu)槟阋钥雌饋砗軓?fù)雜的方式操作一個幾何圖形提供了一個簡單的方法。例如���,你想旋轉(zhuǎn)一個圖像到給定的方向,你知道繞軸2旋轉(zhuǎn)r2角度�,然后繞軸1旋轉(zhuǎn)r1角度���,但你不知道最終的四元數(shù)�,通過使用組合�,你能夠合并兩個旋轉(zhuǎn)為一個單一的四元數(shù),然后,你能夠從原來的點到組合四元數(shù)interpolate來得到一個平滑的轉(zhuǎn)換���。
D3D擴(kuò)展(D3DX)工具庫包含使用四元數(shù)的函數(shù),例如:D3DXQuaternionRatationAxis為一個向量添加一個旋轉(zhuǎn)值,其返回一個D3DXQUATERNION結(jié)構(gòu)體四元數(shù)結(jié)果。另外,D3DXQuaternionMultiply函數(shù)組合四元數(shù)�����,D3DXQuaternionSlerp在兩個四元數(shù)之間執(zhí)行球形線性interpolation�����。
D3D程序能使用下面函數(shù)來簡化四元數(shù)的工作:
D3D程序可以使用下面的函數(shù)來簡化三成分向量的工作: