A decorative fence
Time Limit:1000MS Memory Limit:10000K
Total Submit:1548 Accepted:440
Description
Richard just finished building his new house. Now the only thing the house misses is a cute little wooden fence. He had no idea how to make a wooden fence, so he decided to order one. Somehow he got his hands on the ACME Fence Catalogue 2002, the ultimate resource on cute little wooden fences. After reading its preface he already knew, what makes a little wooden fence cute.
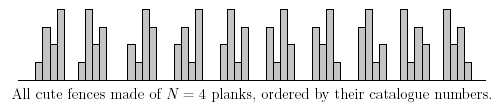
A wooden fence consists of N wooden planks, placed vertically in a row next to each other. A fence looks cute if and only if the following conditions are met:
?The planks have different lengths, namely 1, 2, . . . , N plank length units.
?Each plank with two neighbors is either larger than each of its neighbors or smaller than each of them. (Note that this makes the top of the fence alternately rise and fall.)
It follows, that we may uniquely describe each cute fence with N planks as a permutation a1, . . . , aN of the numbers 1, . . . ,N such that (any i; 1 < i < N) (ai − ai−1)*(ai − ai+1) > 0 and vice versa, each such permutation describes a cute fence.
It is obvious, that there are many di erent cute wooden fences made of N planks. To bring some order into their catalogue, the sales manager of ACME decided to order them in the following way: Fence A (represented by the permutation a1, . . . , aN) is in the catalogue before fence B (represented by b1, . . . , bN) if and only if there exists such i, that (any j < i) aj = bj and (ai < bi). (Also to decide, which of the two fences is earlier in the catalogue, take their corresponding permutations, find the first place on which they differ and compare the values on this place.) All the cute fences with N planks are numbered (starting from 1) in the order they appear in the catalogue. This number is called their catalogue number.
After carefully examining all the cute little wooden fences, Richard decided to order some of them. For each of them he noted the number of its planks and its catalogue number. Later, as he met his friends, he wanted to show them the fences he ordered, but he lost the catalogue somewhere. The only thing he has got are his notes. Please help him find out, how will his fences look like.
Input
The first line of the input file contains the number K (1 <= K <= 100) of input data sets. K lines follow, each of them describes one input data set.
Each of the following K lines contains two integers N and C (1 <= N <= 20), separated by a space. N is the number of planks in the fence, C is the catalogue number of the fence.
You may assume, that the total number of cute little wooden fences with 20 planks fits into a 64-bit signed integer variable (long long in C/C++, int64 in FreePascal). You may also assume that the input is correct, in particular that C is at least 1 and it doesn抰 exceed the number of cute fences with N planks.
Output
For each input data set output one line, describing the C-th fence with N planks in the catalogue. More precisely, if the fence is described by the permutation a1, . . . , aN, then the corresponding line of the output file should contain the numbers ai (in the correct order), separated by single spaces.
Sample Input
2
2 1
3 3
Sample Output
1 2
2 3 1
Source
CEOI 2002
也算是DP+分段統(tǒng)計(jì)中的經(jīng)典題了 呵呵
DP的狀態(tài)表示如下
dp[style][n][i][j] :
style 代表走向 0 代表向上（也就是下次要向下） 1代表向下
n代表總共的fence數(shù)
i代表比當(dāng)前選擇的fence高的fence數(shù)（注意 當(dāng)前fence是一個(gè)隱藏的參數(shù) 因?yàn)樵摖顟B(tài)不需要知道當(dāng)前fence是哪個(gè) 只需要知道有多少比這個(gè)fence高 多少比這個(gè)fence低 就可以代表整個(gè)狀態(tài)）
j代表比當(dāng)前選擇的fence低的fence數(shù)
這樣很直觀的得到了一個(gè)DP方程
dp[0][i][j][k] += dp[1][i-1][j-m][k+m-1]; （m = 1 ... j (inclusive))
dp[1][i][j][k] += dp[0][i-1][j+m-1][k-m]; (m = 1... k(inclusive))
具體請(qǐng)參考源代碼
1
#include <stdio.h>
2#include <string.h>
3
4const int N = 21;
5__int64 dp[2][N][N][N];
6int n;
7__int64 idx;
8bool chk[N];
9
10void pre() {
11 int i, j, m;
12
13 memset(dp, 0, sizeof(dp));
14
15 dp[0][1][0][0] = 1;
16 dp[1][1][0][0] = 1;
17
18 for(i = 2; i <= 20; ++i) {
19 for(j = 0; j < i; ++j) {
20 int k = i - j - 1;
21 for(m = 1; m <= j; ++m)
22 dp[0][i][j][k] += dp[1][i-1][j-m][k+m-1];
23 for(m = 1; m <= k; ++m)
24 dp[1][i][j][k] += dp[0][i-1][j+m-1][k-m];
25 }
26 }
27}
28
29void DFS(int now, int last, int style, __int64 idx) {
30 if(now <= 0) return;
31 int i, j;
32 for(i = 0; i < n; ++i) if(!chk[i]) {
33 if(style == 0 && i < last) continue;
34 if(style == 1 && i > last) return;
35
36 chk[i] = true;
37 int big = 0, small = 0;
38 for(j = 0; j < n; ++j) if(!chk[j]) {
39 if(j < i) small++;
40 if(j > i) big++;
41 }
42
43 if(style == 0 || style == -1) {
44 if(idx > dp[1][now][big][small]) idx -= dp[1][now][big][small];
45 else {
46 printf("%d ", i+1);
47 DFS(now-1, i, 1, idx); return;
48 }
49 }
50
51 if(style == 1 || style == -1) {
52 if(idx > dp[0][now][big][small]) idx -= dp[0][now][big][small];
53 else {
54 printf("%d ", i+1);
55 DFS(now-1, i, 0, idx); return;
56 }
57 }
58 chk[i] = false;
59 }
60}
61
62int main() {
63 int ntc;
64 pre();
65 scanf("%d ", &ntc);
66 while(ntc--) {
67 scanf("%d %I64d", &n, &idx);
68 memset(chk, false, sizeof(chk));
69 DFS(n, -1, -1, idx);
70 putchar('\n');
71 }
72 return 0;
73}