Optimal Keypad
Time Limit:1000MS? Memory Limit:65536K
Total Submit:168 Accepted:80

Description
Optimus Mobiles produces mobile phones that support SMS messages. The Mobiles have a keypad of 12 keys, numbered 1 to 12. There is a character string assigned to each key. To type in the n-th character in the character string of a particular key, one should press the key n times. Optimus Mobiles wishes to solve the problem of assigning character strings to the keys such that for typing a random text out of a dictionary of common words, the average typing effort (i.e. the average number of keystrokes) is minimal.

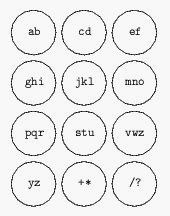
Figure 1

To be more precise, consider a set of characters {a, b, c,..., z, +, *, /, ?} printed on a label tape as in Fig. 2. We want to cut the tape into 12 pieces each containing one or more characters. The 12 labels are numbered 1 to 12 from left to right and will be assigned to the keypad keys in that order.

Figure 2
You are to write a program to find the 11 cutting positions for a given dictionary of common words. The cutting positions should minimize the average number of keystrokes over all common words in the dictionary. Your output should be a string of 11 characters, where character i in this string is the first character of the (i+1)^th label.

Input
The first line contains a single integer t (1 <= t <= 10), the number of test cases. Each test case starts with a line, containing an integer M (1 <= M <= 10000), the number of common words in the test case. In each M subsequent line, there is a common word. Each common word contains at most 30 characters from the alphabet {a, b, c,..., z, +, *, /, ?}.

Output
The output contains one line per test case containing an optimal cut string. Obviously, there may be more than a single optimal cut string, so print the optimal cut string which is the smallest one in lexicographic order.

Sample Input

2
2
hi
ok
5
hello
bye
how
when
who

Sample Output

bcdefghijko
bcdefhlnowy

Source
Tehran 2003

#include? < iostream >
using ? namespace ?std;

const ? int ?INF? = ? 100000000 ;

int ?f[ 13 ][ 30 ][ 30 ];
int ?s[ 13 ][ 30 ][ 30 ];
int ?l[ 13 ][ 30 ][ 30 ];
char ?c[]? = ? { ' a ' ,? ' b ' ,? ' c ' ,? ' d ' ,? ' e ' ,? ' f ' ,? ' g ' ,? ' h ' ,? ' i ' ,? ' j ' ,? ' k ' ,? ' l ' ,? ' m ' ,? ' n ' ,? ' o '
????????????,? ' p ' ,? ' q ' ,? ' r ' ,? ' s ' ,? ' t ' ,? ' u ' ,? ' v ' ,? ' w ' ,? ' x ' ,? ' y ' ,? ' z ' ,? ' + ' ,? ' * ' ,? ' / ' ,? ' ? ' } ;

void ?OutPut( int ?k,? int ?i,? int ?j)
{
???? if ?(l[k][i][j]? >= ? 0 )
???? {
????????OutPut(l[k][i][j],?i,?s[k][i][j]);
????
????????printf( " %c " ,?c[s[k][i][j] + 1 ]);
????????
????????OutPut(k - l[k][i][j],?s[k][i][j] + 1 ,?j);????
????}
}

void ?Solve()
{
???? int ?n;
???? int ?i,?j,?k,?p,?q,?t,?e;
???? int ?cntLable[ 300 ]? = ? { 0 } ;
???? int ?sum;
???? char ?tmpS[ 31 ];
????scanf( " %d " ,? & n);
???? for ?(i = 0 ;?i < n;?i ++ )
???? {
????????scanf( " %s " ,?tmpS);
???????? for ?(j = 0 ;?j < strlen(tmpS);?j ++ )
????????????cntLable[tmpS[j]] ++ ;
????}

???? for ?(k = 1 ;?k <= 12 ;?k ++ )
???????? for ?(i = 0 ;?i < 30 ;?i ++ )
???????????? for ?(j = 0 ;?j < 30 ;?j ++ )
???????????? {
????????????????f[k][i][j]? = ?INF;
????????????????s[k][i][j]? = ? - 1 ;
????????????????l[k][i][j]? = ? - 1 ;
????????????}

???? // init?k=1
???? for ?(i = 0 ;?i < 30 ;?i ++ )
???? {
????????sum? = ? 0 ;
???????? for ?(j = i,?k = 1 ;?j < 30 ;?j ++ ,?k ++ )
???????? {
????????????sum? += ?cntLable[c[j]]? * ?k;
????????????f[ 1 ][i][j]? = ?sum;
????????}
????}

???? for ?(k = 2 ;?k <= 12 ;?k ++ )
???????? for ?(i = 0 ;?i < 30 ;?i ++ )
???????????? for ?(j = i + k - 1 ;?j < 30 ;?j ++ )
???????????? {
???????????????? for ?(t = i;?t < j;?t ++ )
???????????????? {
????????????????????e? = ?k - 1 ? < ?t - i + 1 ? ? ?k - 1 ?:?t - i + 1 ;
???????????????????? for ?(p = 1 ;?p <= e;?p ++ )
???????????????????????? if ?(f[k][i][j]? > ?f[p][i][t]? + ?f[k - p][t + 1 ][j])
???????????????????????? {
????????????????????????????f[k][i][j]? = ?f[p][i][t]? + ?f[k - p][t + 1 ][j];
????????????????????????????s[k][i][j]? = ?t;
????????????????????????????l[k][i][j]? = ?p;
????????????????????????}
????????????????}
????????????}

????OutPut( 12 ,? 0 ,? 29 );
????printf( " \n " );
}

int ?main()
{
???? int ?n;
????scanf( " %d " ,? & n);
???? while ?(n -- ? != ? 0 )
???? {
????????Solve();
????}
???? return ? 0 ;
}