- Introduction
- The Idea
- The Gaussian Case
- Experiments with Black-and-White Images
- Experiments with Color Images
- References
Introduction
Filtering is perhaps the most fundamental operation of image processing and computer vision. In the broadest sense of the term "filtering", the value of the filtered image at a given location is a function of the values of the input image in a small neighborhood of the same location. For example, Gaussian low-pass filtering computes a weighted average of pixel values in the neighborhood, in which the weights decrease with distance from the neighborhood center. Although formal and quantitative explanations of this weight fall-off can be given, the intuition is that images typically vary slowly over space, so near pixels are likely to have similar values, and it is therefore appropriate to average them together. The noise values that corrupt these nearby pixels are mutually less correlated than the signal values, so noise is averaged away while signal is preserved.
The assumption of slow spatial variations fails at edges, which are consequently blurred by linear low-pass filtering. How can we prevent averaging across edges, while still averaging within smooth regions? Many efforts have been devoted to reducing this undesired effect. Bilateral filtering is a simple, non-iterative scheme for edge-preserving smoothing.
Back to Index
The Idea
The basic idea underlying bilateral filtering is to do in the range of an image what traditional filters do in its domain. Two pixels can be close to one another, that is, occupy nearby spatial location, or they can be similar to one another, that is, have nearby values, possibly in a perceptually meaningful fashion.
Consider a shift-invariant low-pass domain filter applied to an image:
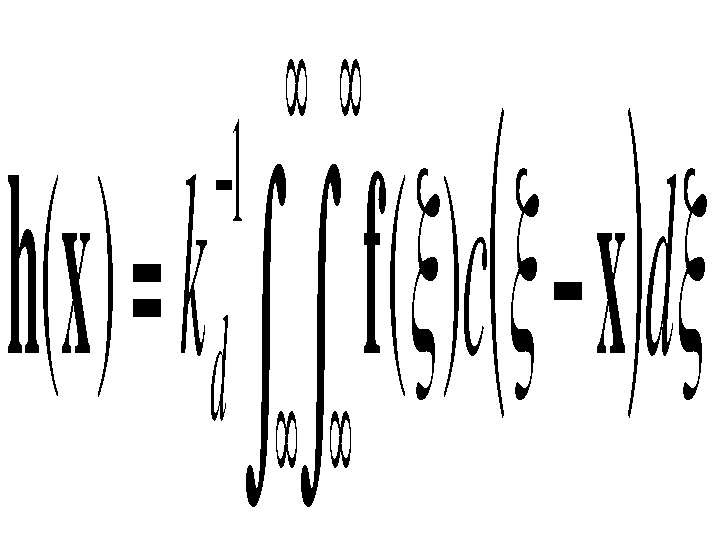
The bold font for f and h emphasizes the fact that both input and output images may be multi-band. In order to preserve the DC component, it must be
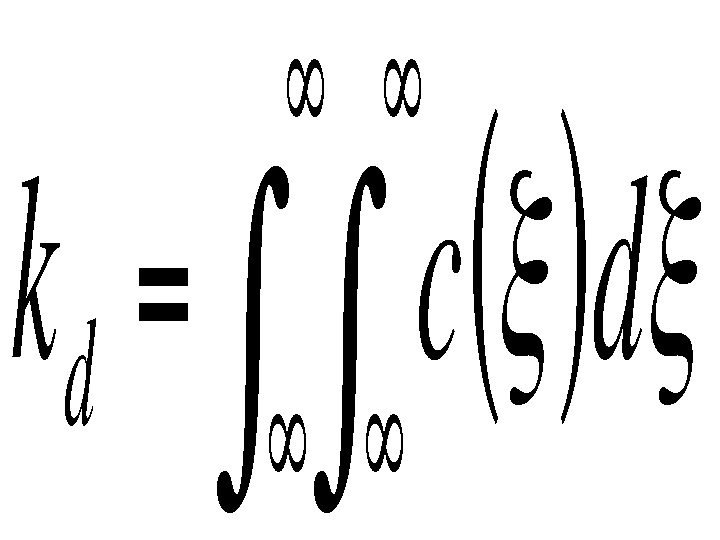
Range filtering is similarly defined:
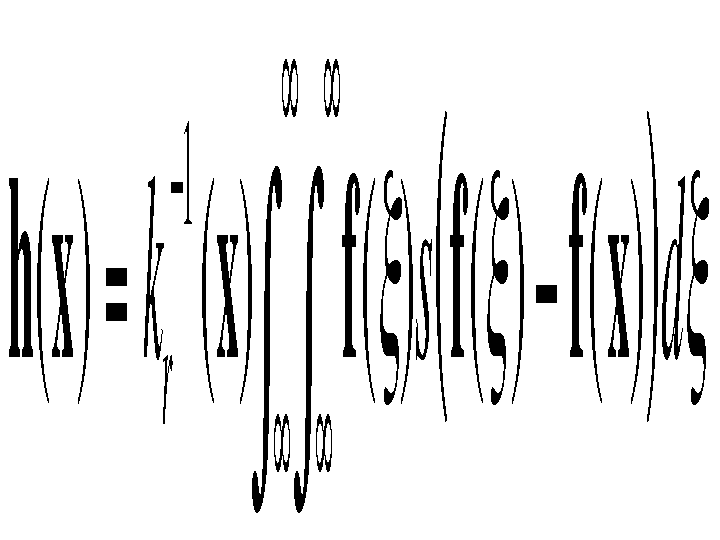
In this case, the kernel measures the photometric similarity between pixels. The normalization constant in this case is

The spatial distribution of image intensities plays no role in range filtering taken by itself. Combining intensities from the entire image, however, makes little sense, since the distribution of image values far away from x ought not to affect the final value at x. In addition, one can show that range filtering without domain filtering merely changes the color map of an image, and is therefore of little use. The appropriate solution is to combine domain and range filtering, thereby enforcing both geometric and photometric locality. Combined filtering can be described as follows:
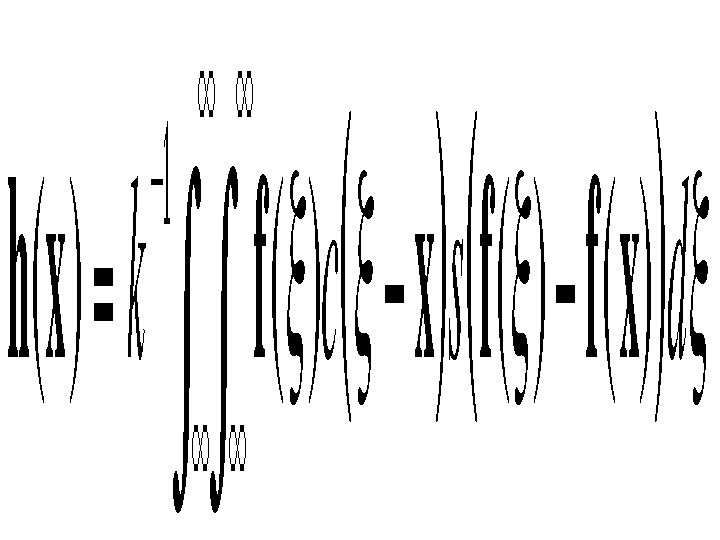
with the normalization
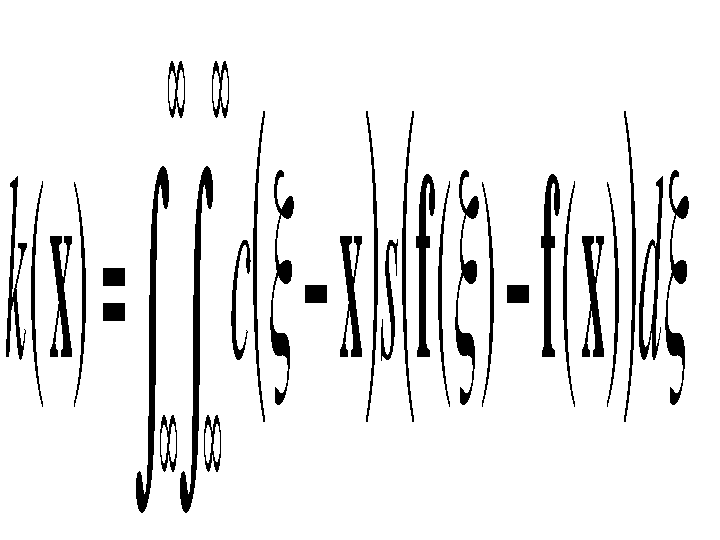
Combined domain and range filtering will be denoted as bilateral filtering. It replaces the pixel value at x with an average of similar and nearby pixel values. In smooth regions, pixel values in a small neighborhood are similar to each other, and the bilateral filter acts essentially as a standard domain filter, averaging away the small, weakly correlated differences between pixel values caused by noise. Consider now a sharp boundary between a dark and a bright region, as in figure 1(a).
When the bilateral filter is centered, say, on a pixel on the bright side of the boundary, the similarity function s assumes values close to one for pixels on the same side, and values close to zero for pixels on the dark side. The similarity function is shown in figure 1(b) for a 23x23 filter support centered two pixels to the right of the step in figure 1(a). The normalization term k(x) ensures that the weights for all the pixels add up to one. As a result, the filter replaces the bright pixel at the center by an average of the bright pixels in its vicinity, and essentially ignores the dark pixels. Conversely, when the filter is centered on a dark pixel, the bright pixels are ignored instead. Thus, as shown in figure 1(c), good filtering behavior is achieved at the boundaries, thanks to the domain component of the filter, and crisp edges are preserved at the same time, thanks to the range component.
Back to Index
The Gaussian Case
A simple and important case of bilateral filtering is shift-invariant Gaussian filtering, in which both the closeness function c and the similarity function s are Gaussian functions of the Euclidean distance between their arguments. More specifically, c is radially symmetric:
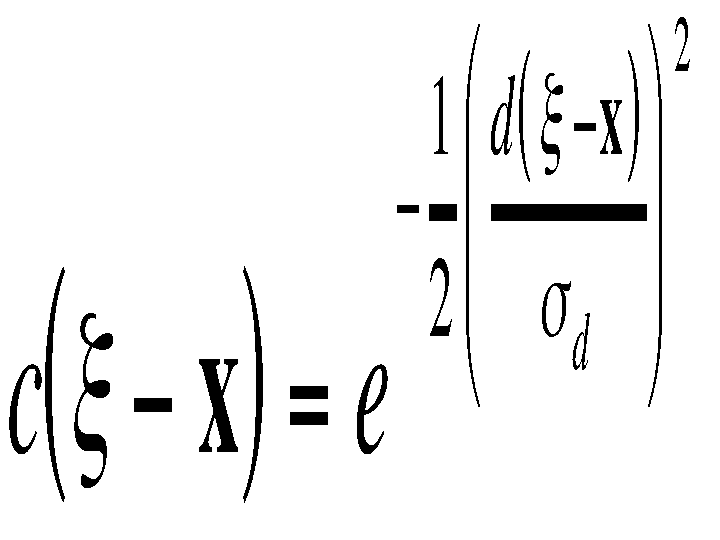
where
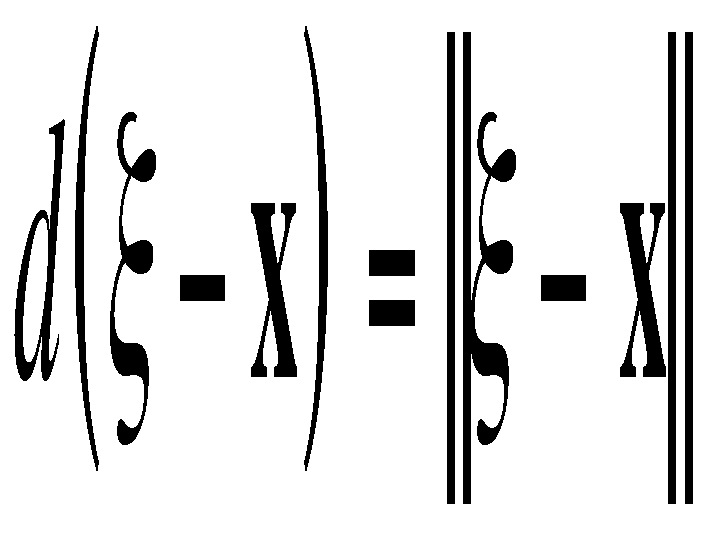
is the Euclidean distance. The similarity function s is perfectly analogous to c :
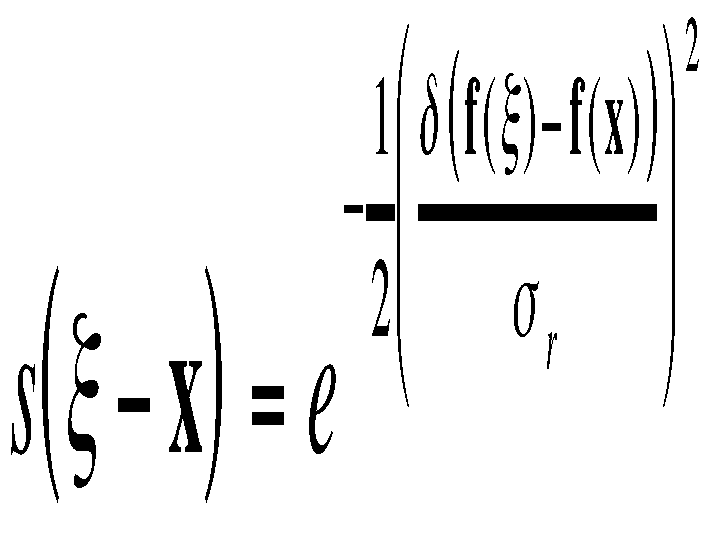
where
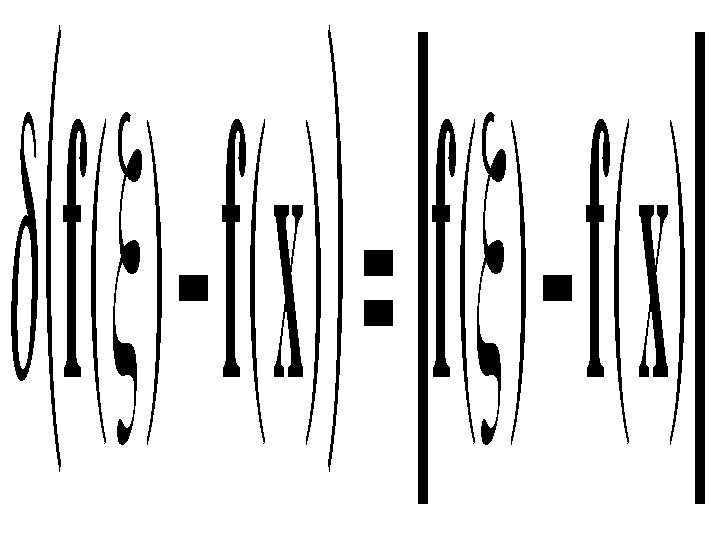
is a suitable measure of distance in intensity space. In the scalar case, this may be simply the absolute difference of the pixel difference or, since noise increases with image intensity, an intensity-dependent version of it. Just as this form of domain filtering is shift-invariant, the Gaussian range filter introduced above is insensitive to overall additive changes of image intensity. Of course, the range filter is shift-invariant as well.
Back to Index
Experiments with Black-and-White Images
Figure 2 (a) and (b) show the potential of bilateral filtering for the removal of texture. The picture "simplification" illustrated by figure 2 (b) can be useful for data reduction without loss of overall shape features in applications such as image transmission, picture editing and manipulation, image description for retrieval.
|

|
|

|
|
(a) |
|
(b) |
|
|
Figure 2 |
|
Bilateral filtering with parameters sd =3 pixels and sr =50 intensity values is applied to the image in figure 3 (a) to yield the image in figure 3 (b). Notice that most of the fine texture has been filtered away, and yet all contours are as crisp as in the original image. Figure 3 (c) shows a detail of figure 3 (a), and figure 3 (d) shows the corresponding filtered version. The two onions have assumed a graphics-like appearance, and the fine texture has gone. However, the overall shading is preserved, because it is well within the band of the domain filter and is almost unaffected by the range filter. Also, the boundaries of the onions are preserved.
Back to Index
Experiments with Color Images
For black-and-white images, intensities between any two gray levels are still gray levels. As a consequence, when smoothing black-and-white images with a standard low-pass filter, intermediate levels of gray are produced across edges, thereby producing blurred images. With color images, an additional complication arises from the fact that between any two colors there are other, often rather different colors. For instance, between blue and red there are various shades of pink and purple. Thus, disturbing color bands may be produced when smoothing across color edges. The smoothed image does not just look blurred, it also exhibits odd-looking, colored auras around objects.
Figure 4 (a) shows a detail from a picture with a red jacket against a blue sky. Even in this unblurred picture, a thin pink-purple line is visible, and is caused by a combination of lens blurring and pixel averaging. In fact, pixels along the boundary, when projected back into the scene, intersect both red jacket and blue sky, and the resulting color is the pink average of red and blue. When smoothing, this effect is emphasized, as the broad, blurred pink-purple area in figure 4 (b) shows.
To address this difficulty, edge-preserving smoothing could be applied to the red, green, and blue components of the image separately. However, the intensity profiles across the edge in the three color bands are in general different. Smoothing the three color bands separately results in an even more pronounced pink and purple band than in the original, as shown in figure 4 (c). The pink-purple band, however, is not widened as in the standard-blurred version of figure 4 (b).
A much better result can be obtained with bilateral filtering. In fact, a bilateral filter allows combining the three color bands appropriately, and measuring photometric distances between pixels in the combined space. Moreover, this combined distance can be made to correspond closely to perceived dissimilarity by using Euclidean distance in the CIE-Lab color space. This color space is based on a large body of psychophysical data concerning color-matching experiments performed by human observers. In this space, small Euclidean distances are designed to correlate strongly with the perception of color discrepancy as experienced by an "average" color-normal human observer. Thus, in a sense, bilateral filtering performed in the CIE-Lab color space is the most natural type of filtering for color images: only perceptually similar colors are averaged together, and only perceptually important edges are preserved. Figure 4 (d) shows the image resulting from bilateral smoothing of the image in figure 4 (a). The pink band has shrunk considerably, and no extraneous colors appear.
Figure 5 (c) shows the result of five iterations of bilateral filtering of the image in figure 5 (a). While a single iteration produces a much cleaner image (figure 5 (b)) than the original, and is probably sufficient for most image processing needs, multiple iterations have the effect of flattening the colors in an image considerably, but without blurring edges. The resulting image has a much smaller color map, and the effects of bilateral filtering are easier to see when displayed on a printed page. Notice the cartoon-like appearance of figure 5 (c). All shadows and edges are preserved, but most of the shading is gone, and no "new" colors are introduced by filtering.
Back to Index
References
[1] C. Tomasi and R. Manduchi, "Bilateral Filtering for Gray and Color Images", Proceedings of the 1998 IEEE International Conference on Computer Vision, Bombay, India.
[2] T. Boult, R.A. Melter, F. Skorina, and I. Stojmenovic,"G-neighbors", Proceedings of the SPIE Conference on Vision Geometry II, pages 96-109, 1993.
[3] R.T. Chin and C.L. Yeh, "Quantitative evaluation of some edge-preserving noise-smoothing techniques", Computer Vision, Graphics, and Image Processing, 23:67-91, 1983.
[4] L.S. Davis and A. Rosenfeld, "Noise cleaning by iterated local averaging", IEEE Transactions on Systems, Man, and Cybernetics, 8:705-710, 1978.
[5] R.E. Graham, "Snow-removal - a noise-stripping process for picture signals", IRE Transactions on Information Theory, 8:129-144, 1961.
[6] N. Himayat and S.A. Kassam, "Approximate performance analysis of edge preserving filters", IEEE Transactions on Signal Processing, 41(9):2764-77, 1993.
[7] T.S. Huang, G.J. Yang, and G.Y. Tang, "A fast two-dimensional median filtering algorithm", IEEE Transactions on Acoustics, Speech, and Signal Processing, 27(1):13-18, 1979.
[8] J.S. Lee, "Digital image enhancement and noise filtering by use of local statistics", IEEE Transactions on Pattern Analysis and Machine Intelligence, 2(2):165-168, 1980.
[9] M. Nagao and T. Matsuyama, "Edge preserving smoothing", Computer Graphics and Image Processing, 9:394-407, 1979.
[10] P.M. Narendra, "A separable median filter for image noise smoothing", IEEE Transactions on Pattern Analysis and Machine Intelligence, 3(1):20-29, 1981.
[11] K.J. Overton and T.E. Weymouth, "A noise reducing preprocessing algorithm",Proceedings of the IEEE Computer Science Conference on Pattern Recognition and Image Processing, pages 498-507, Chicago, IL, 1979.
[12] P. Perona and J. Malik, "Scale-space and edge detection using anisotropic diffusion", IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(7):629-639, 1990.
[13] G. Ramponi, "A rational edge-preserving smoother", Proceedings of the International Conference on Image Processing, volume 1, pages 151-154, Washington, DC, 1995.
[14] G. Sapiro and D.L. Ringach, "Anisotropic diffusion of color images", Proceedings of the SPIE, volume 2657, pages 471-382, 1996.
[15] D.C.C. Wang, A.H. Vagnucci, and C.C. Li, "A gradient inverse weighted smoothing scheme and the evaluation of its performance", Computer Vision, Graphics, and Image Processing, 15:167-181, 1981.
[16] G. Wyszecki and W. S. Styles, Color Science: Concepts and Methods, Quantitative Data and Formulae, John Wiley and Sons, New York, NY, 1982.
[17] L. Yin, R. Yang, M. Gabbouj, and Y. Neuvo, "Weighted median filters: a tutorial",IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 43(3):155-192, 1996.