這本書對于入門級的人來說是一個不錯的選擇,它囊括了很多關于計算機方面的知識���,能夠使你對這方面的知識有個廣泛的了解。
對于小數的存儲常用的是浮點記數法。
浮點記數法簡介
對于知識的掌握���,通過例子的學習是一個很好的方式。為了考慮到例子的簡易型,用一個字節來存儲浮點數��。那么如01101011這樣的二進制序列表示的是什么小數呢�����?
一個字節中浮點記數法有如下成分:
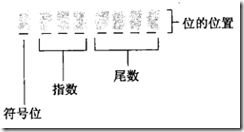
在01101011這么一個串中�����,符號位是0表示非負,1則表示負��,指數為110�����,表示位數將乘以2^(指數)�����,也就是將小數點從尾數位的最左邊移動指數個位,如果指數為正,向右移動�����;反之��,向左移動指數位���。110是用余碼的方式進行記錄的�����。對于余碼���,我采用的解析的方式是,將最高為取反�����,按照補碼的方式進行讀取�����。
110--->010���,表示2���;0100--->1100�����,表示-4;
既然提到了補碼,就解釋一下補碼��,最高位為零的補碼其值直接讀取�����,0110--->6��;最高為為1的補碼,其值的讀取方式���,從右往左遇到第一個1之后的所有位取反,讀出值后加個負號��,1101--->0011��,則-3。當然對于0和最小的負數�����,不適合上述的方式��,但是也很容易就能給出其值�����。
再讓我們回到0,110,1011這個串中,尾數.1011最左斷含有一個小數點�����,由于110--->2�����,因此小數點向右移動兩位則10.11���,此時讀取值2+1/2+1/4=2又3/4��。
至此,我們已經知道小數是如何存儲在二進制串中��,也知道了如何將其轉換為10進制數值�����,那么該提出注意事項的時候了�����。
1. 規范化形式
尾數最左端的一位必須是1��,否則會出現多意的現象��。如00111100,01000110�����,都可以解碼為3/8。
2. 截斷誤差
整型值會出現溢出現象���,同樣浮點數也會出現類似的現象。如利用一字節浮點記數法存儲值2又5/8�����,先用二進制進行表示10.101���,而尾數只有4位��,因此會出現截斷��。
還有一個需要注意的是浮點記數法表示的數值加法中,它們相加的順序很重要���。
如,2+1/4+1/8+1/8+1/8+1/8,當到2(5/8)+1/8時���,2(5/8)用二進制表示為10.101,這將發生截斷��,變成10.10��,繼續加1/8則會持續階段���。當反過來進行加法運算時,則不會出現截斷的現象。
由于實際浮點數具有較長的位數�����,能夠較好的運用于一般的浮點數運算中�����。但是這樣的問題在一些應用中是很嚴重的(如航海系統),小的誤差在不斷的加法運算中累加���,最終產生嚴重的后果���,因此對于精度要求較好的運算中��,可以選擇采用分數表示法,分裝一個表示分數的類。