原文：http://www.cnblogs.com/JCSU/articles/1449986.html

?

一、線性代數(shù)基本方程組

?

基本方程組：

?

矩陣表示：

?

?

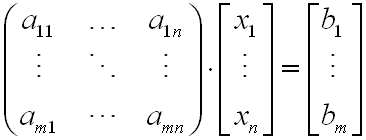解決問題的視角：

?

1、解聯(lián)立方程的視角 (行階梯變換 & ?矩陣運(yùn)算)

著重研究解x，即研究線性方程組的解法。中學(xué)里的解方程和MATLAB的矩陣除法就是這樣。

要點(diǎn)：矩陣的每一行代表一個(gè)方程，m行代表m個(gè)線性聯(lián)立方程。 n列代表n個(gè)變量。如果m是獨(dú)立方程數(shù)，根據(jù)m<n、m=n、m>n確定方程是 ‘欠定’、‘適定’ 還是 ‘超定’。對(duì)這三種情況都會(huì)求解了，研究就完成了。必須剔除非獨(dú)立方程。行階梯形式、行列式和秩的概念很大程度上為此目的而建立。

?

2、向量空間中向量的合成的視角 (用向量空間解方程組)

把A各列看成n個(gè)m維基本向量，線性方程組看成基向量的線性合成：

要點(diǎn)：解x是這些基向量的系數(shù)。它可能是常數(shù)(適定方程)，也可能成為其中的一個(gè)子空間(欠定方程) 。要建立其幾何概念，并會(huì)求解或解空間。

?

3、線性變換或映射的視角 (線性變換及其特征)

把b看成變量y，著重研究把Rn空間的x變換為Rm空間y 的效果，就是研究線性變換系數(shù)矩陣A的特征對(duì)變換的影響。

?

要點(diǎn)：就是要找到適當(dāng)?shù)淖儞Q，使研究問題的物理意義最為明晰。特征值問題就是一例。

?

?

• Leontief教授把美國的經(jīng)濟(jì)用500個(gè)變量的500個(gè)線性方程來描述，在1949年利用當(dāng)時(shí)的計(jì)算機(jī)解出了42×42的簡化模型，使他于1973年獲得諾貝爾經(jīng)濟(jì)獎(jiǎng)，從而大大推動(dòng)了線性代數(shù)的發(fā)展。

• 把飛行器的外形分成若干大的部件，每個(gè)部件沿著其表面又用三維的細(xì)網(wǎng)格劃分出許多立方體，這些立方體包括了機(jī)身表面以及此表面內(nèi)外的空氣。對(duì)每個(gè)立方體列寫出空氣動(dòng)力學(xué)方程，其中包括了與它相鄰的立方體的共同邊界變量，這些方程通常都已經(jīng)簡化為線性方程。對(duì)一個(gè)飛行器，小立方體的數(shù)目可以多達(dá)400,000個(gè)，而要解的聯(lián)立方程可能多達(dá)2,000,000個(gè)。

• 飛行器的運(yùn)動(dòng)要用三個(gè)轉(zhuǎn)動(dòng)和三個(gè)平移共六個(gè)變量來表示（像在第九章中介紹的那樣）。除此以外，為了控制飛行器的三維轉(zhuǎn)動(dòng)，需要三個(gè)控制面，即方向舵（垂直尾翼）、升降舵（水平尾翼）和副翼，它們的偏轉(zhuǎn)角又構(gòu)成了三個(gè)變量。描述飛行器的運(yùn)動(dòng)就需要12個(gè)變量的組合。而且這已經(jīng)不單是代數(shù)方程，而是微分方程了。

• 衛(wèi)星上用三種可見光和四種紅外光進(jìn)行攝像，對(duì)每一個(gè)區(qū)域，可以獲得七張遙感圖象。利用多通道的遙感圖可以獲取盡可能多的地面信息，因?yàn)楦鞣N地貌、作物和氣象特征可能對(duì)不同波段的光敏感。而在實(shí)用上應(yīng)該尋找每一個(gè)地方的主因素，成為一張實(shí)用的圖象。每一個(gè)象素上有七個(gè)數(shù)據(jù)，形成一個(gè)多元的變量數(shù)組，在其中合成并求取主因素的問題，就與線性代數(shù)中要討論的特征值問題有關(guān)。

• 在全國設(shè)立幾十萬個(gè)觀察點(diǎn)，把每一點(diǎn)的經(jīng)度、緯度和高度三個(gè)坐標(biāo)建立起來。現(xiàn)在對(duì)于經(jīng)度緯度的測(cè)量精度要求，已經(jīng)提高到了若干厘米，對(duì)于高度的精度要求更高。在一些邊遠(yuǎn)地區(qū)，對(duì)于一些特征點(diǎn)的測(cè)量，要耗費(fèi)很大的人力物力。例如對(duì)珠穆朗瑪峰頂高度的測(cè)量，要經(jīng)過多種方法，取得多種數(shù)據(jù)，并且用最小二乘法進(jìn)行誤差的處理。

?

?

三、行階梯法解線性方程

?

?

1、線性方程的Matlab表示方法

?

(1) 由n個(gè)變量組成的m個(gè)聯(lián)立線性代數(shù)方程組：

?

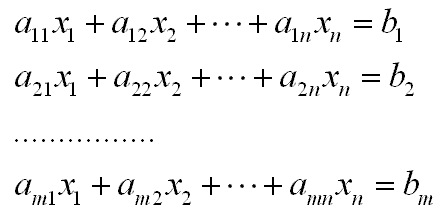
用MATLAB語言表示為：

其中：

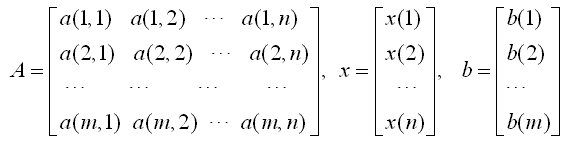
n是未知數(shù)個(gè)數(shù)，m是獨(dú)立方程的個(gè)數(shù)。當(dāng)m<n時(shí)，方程組有無數(shù)多個(gè)解，稱為欠定方程；當(dāng)m>n時(shí)，方程組無解，稱為超定方程；當(dāng)m=n時(shí)，方程組有唯一解，稱為適定方程；所以不能簡單地看形式上的m和n，還必須剔除其中非獨(dú)立方程的虛假成分。將要討論的行階梯形式、行列式和“秩”等概念，很大程度上就是為了找到獨(dú)立方程的數(shù)目。

?

(2) 解線性方程組及在matlab中的顯示

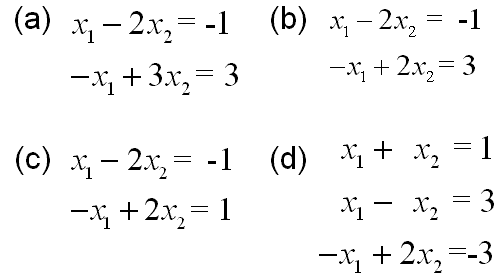
作圖的matlab代碼：

使用參考：ezplot

?

四個(gè)方程組在matlab中的作圖：

?

?

2、初等行變換

?

將系數(shù)矩陣A和B組成增廣矩陣：

?

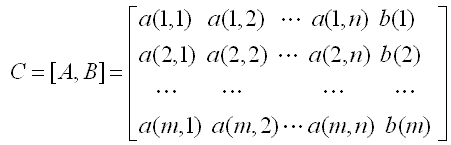對(duì)增廣矩陣的行作以下三種運(yùn)算不會(huì)改變方程組的解，這三種運(yùn)算組成了矩陣的初等行變換：

(1) 行交換：將增廣矩陣的第 i , j 兩行互換位置。MATLAB語句：c([i,j],:) = c([j,i],:)

(2) 行乘數(shù)：將增廣矩陣的第 i 行乘以常數(shù) k 。MATLAB語句：c(i,:) = k*c(i,:)

(3) 行相加：將增廣矩陣的第 i 行乘以常數(shù) k，加到第 j 行。MATLAB語句：c(j,:) = c(j,:) + k*c(i,:)

?

?

3、行階梯矩陣的生成(高斯消元過程)

?

(1) 行階梯矩陣、簡化行階梯矩陣

?

如果線性方程組的左端系數(shù)具有以下三個(gè)特點(diǎn)：

a) 所有非零行都處在全零行的上方；

b) 各行的第一個(gè)非零元素的列號(hào)比其上方所有各行的第一非零元素的列號(hào)都要大；

c) 所有的第一非零元素所在的列中，其下方的所有元素均為零；

這樣的矩陣稱為行階梯矩陣(或上三角矩陣)，如矩陣C1：

?

?

?

如果行階梯矩陣還滿足以下兩個(gè)額外特點(diǎn)，則稱之為簡化行階梯矩陣，如下圖的矩陣C2：

1)?各行的第一個(gè)非零元素是所在列中唯一的非零元素

2)?各行的第一個(gè)非零元素都等于1

?

(2) 高斯消元過程、實(shí)例、matlab消元

步驟1：把主對(duì)角線下方第一列元素全變?yōu)榱恪Ｔ诰仃嚨母餍兄校x擇第1列元素的絕對(duì)值最大的行，通過行交換把它放到第1行（這樣做主要是為了提高計(jì)算精度，如果不考慮精度，只要第1行第1列元素不為零，可以跳過這個(gè)環(huán)節(jié)）。以第1行為基準(zhǔn)，依次把第2行至第n行的第1列的元素消為零。

步驟2：在2~n行中，選擇第2列元素的絕對(duì)值最大的行，通過行交換把它放到第2行。以第2行為基準(zhǔn)行，依次把第3行至第n行的第2列的元素消為零。

步驟3: 做法同前面的步驟

...

步驟n-1：做法同前面的步驟

?

實(shí)例：用行階梯及回代法求解以下方程組(方程組對(duì)應(yīng)的增廣矩陣已給出)：

?

matlab消元程序：

?

?

matlab中的消元過程如下：

?

?

?

4、MATLAB中的行階梯生成函數(shù)

MATLAB已經(jīng)把“簡化行階梯形式(reduced row echelon form)”的計(jì)算過程集成為一個(gè)子程序rref。它的輸入變?cè)梢允蔷€性方程組的系數(shù)矩陣，也可以是其增廣矩陣，輸入U(xiǎn)=rref([A,b])，輸出結(jié)果就是簡化行階梯矩陣。

?

例：用MATLAB中的rref求解3(2)中的方程組：

?

解得：x1=-0.0236,?? x2=0.7508,?? x3=-0.2828

?

?

5、行階梯法解欠定方程組

上面討論的是方程數(shù)m與變量數(shù)n相等的情況。普遍情況下，m<n，屬于欠定方程，方程將有無數(shù)解，我們必須找出其解的一般形式。即使m=n，也有可能是假象，因?yàn)橛械姆匠淌窍嘁赖模?strong>有效方程數(shù)也許小于m。要看清它究竟是什么類型，應(yīng)該看行階梯形式的結(jié)果，即有效行的數(shù)目，有效行的個(gè)數(shù)也叫矩陣的“秩”。對(duì)于一個(gè)矩陣，盡管因變換的次序不同，但“秩”是唯一的。

對(duì)增廣矩陣C=[A, b]進(jìn)行行階梯變換，得到的行階梯矩陣U的下方可能有全零出現(xiàn)。行階梯形式為：

其中，U為方程中左端的系數(shù)矩陣，d為方程右端的常數(shù)項(xiàng)。當(dāng)U中某行各變量系數(shù)全為零時(shí)，d中的對(duì)應(yīng)行也必須為零，否則就構(gòu)成了等式左右不相等的矛盾方程。因此，矩陣A和增廣矩陣[A,b]的行階梯形式U(或簡化行階梯矩陣)應(yīng)當(dāng)有同樣的全零行，也就是兩者有同樣的秩，這是方程組有解的必要條件。

原來的m行中只剩下r個(gè)非全零行，意味著m個(gè)方程中只有r個(gè)有效，也就是它的秩為r，m-r個(gè)全零行反映了原方程組中有m-r個(gè)是相依方程，最后U中有效的部分是r×n矩陣，就是r個(gè)方程和n個(gè)未知數(shù)。因?yàn)閞<n，這是一個(gè)欠定方程組，n個(gè)未知數(shù)(變量)中有n-r個(gè)可以任意設(shè)定，我們稱這些未知數(shù)為自由變量，也可把它們稱為任意常數(shù)。

?

例：解下列方程組

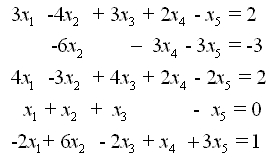
輸入系數(shù)矩陣A和常數(shù)矩陣b，求增廣矩陣的簡化行階梯形式，MATLAB代碼如下：

?

運(yùn)行過程如下：

?

從U0可知，下方有兩個(gè)全零行，說明原方程中有兩個(gè)方程是相依的，只有三個(gè)獨(dú)立方程，此時(shí)各行首非零元素不在對(duì)主角線上，列號(hào)分別為1，2，4。我們應(yīng)當(dāng)把x1, x2, x4看作待求的變量，而把其余的兩個(gè)變量x3和x5看作自由變量。

把U恢復(fù)成方程形式并移項(xiàng)，使左端只包含待求變量，把x3和x5移到等式右邊：

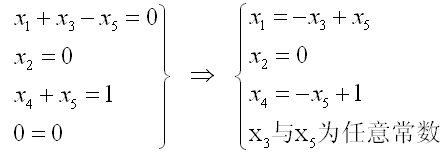
如果要給出一個(gè)具體解，通常取自由變量x3和x5為零，這樣得出的解是x1=x2=x3=x5=0, x4=-1。但這樣來表示方程的解容易造成誤會(huì)，以為方程組只有一個(gè)解。所以比較嚴(yán)格的表示方法是取自由變量x3和x5為c1和c2:

x3=c1,? x5=c2,? x1=-c1+c2,? x2=0,? x4=-c2+1

這樣，選擇不同的c1和c2，就可以得出不同的解，所以其解有無數(shù)組。由于它包含兩個(gè)自由變量，因此在兩個(gè)自由度上都可以在（-∞,+∞）范圍內(nèi)變化，從幾何上說，它的解占據(jù)了一個(gè)兩維空間(平面)。

解的最后形式：

?

?

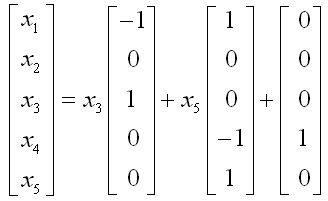
5、應(yīng)用實(shí)例

?

(1) 平板穩(wěn)態(tài)溫度的計(jì)算

?

研究一個(gè)平板的熱傳導(dǎo)問題，設(shè)該平板的周邊溫度已經(jīng)知道（見下圖），現(xiàn)在要確定板中間4個(gè)點(diǎn)a,b,c,d處的溫度。假定其熱傳導(dǎo)過程已經(jīng)達(dá)到穩(wěn)態(tài)，因此在均勻的網(wǎng)格點(diǎn)上，各點(diǎn)的溫度是其上下左右4個(gè)點(diǎn)的溫度的平均值。

根據(jù)題意列出方程為：

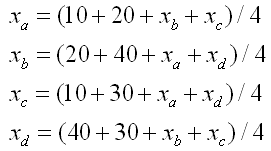
移項(xiàng)整理為標(biāo)準(zhǔn)的矩陣形式為：

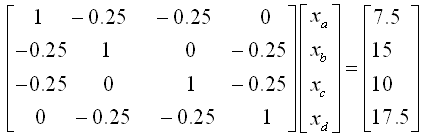
輸入MATLAB程度計(jì)算為：

?

把它“翻譯”為方程，即有：xa=20℃，xb=27.5℃，xc=22.5℃，xd=30℃

?

?

(2) 化學(xué)方程式配平

?

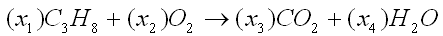
建立一個(gè)向量方程組，每個(gè)方程分別描述一種原子在反應(yīng)前后的數(shù)目。在上面的方程中，有碳、氫、氧三種元素需要配平，構(gòu)成了三個(gè)方程。而有四種物質(zhì)，其數(shù)量用四個(gè)變量x1,x2,x3,x4來表示。將每種物質(zhì)中的元素原子數(shù)按碳、氫、氧順序排列，可以寫出：

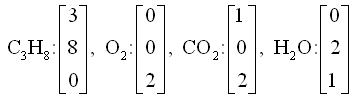
要使方程配平，x1,x2,x3,x4必須滿足：

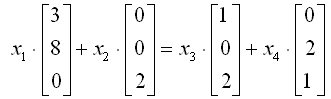
寫成矩陣方程：

對(duì)A進(jìn)行行階梯變換：

?

要注意這四個(gè)列對(duì)應(yīng)于四個(gè)變量的系數(shù)，所以這三行系數(shù)對(duì)應(yīng)的方程是：

x₁????????? -0.2500x₄ = 0
??? x₂????? -1.2500x₄ = 0
??????? x₃? -0.7500x₄ = 0

即x4是自由變量。因?yàn)榛瘜W(xué)家們喜歡把方程的系數(shù)取為最小整數(shù)，此處可取x4=4，則x1,x2,x3均有整數(shù)解，x1=1, x2=5, x3=3。?

對(duì)于比較復(fù)雜的反應(yīng)過程，為了便于得到最小整數(shù)解，在解化學(xué)配平的線性方程組時(shí)，應(yīng)該在MATLAB中先規(guī)定取有理分式格式，即先輸入format rat，這樣就很容易看出應(yīng)令x4=4。結(jié)果為：

?

?

(3) 交通流量分析

某城市有兩組單行道，構(gòu)成了一個(gè)包含四個(gè)節(jié)點(diǎn)A,B,C,D的十字路口，如下圖所示。在交通繁忙時(shí)段的汽車從外部進(jìn)出此十字路口的流量（每小時(shí)的車流數(shù)）標(biāo)于圖上。現(xiàn)要求計(jì)算每兩個(gè)節(jié)點(diǎn)之間路段上的交通流量x1, x2, x3, x4。

解：

在每個(gè)節(jié)點(diǎn)上，進(jìn)入和離開的車數(shù)應(yīng)該相等，這就決定了四個(gè)節(jié)點(diǎn)的流通方程：