樹狀數組
武鋼三中 吳豪
【引言】
在解題過程中,我們有時需要維護一個數組的前綴和S[i]=A[1]+A[2]+...+A[i]。
但是不難發現,如果我們修改了任意一個A[i],S[i]、S[i+1]...S[n]都會發生變化。
可以說,每次修改A[i]后,調整前綴和S[]在最壞情況下會需要O(n)的時間。
當n非常大時,程序會運行得非常緩慢。
因此,這里我們引入“樹狀數組”,它的修改與求和都是O(logn)的,效率非常高。
【理論】
為了對樹狀數組有個形 象的認識,我們先看下面這張圖。
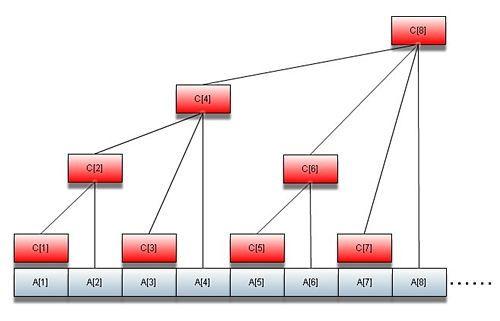
如圖所示,紅色矩形表示的數組C[]就是樹狀數組。
這里,C[i]表示A[i-2^k+1]到A[i]的和,而k則是i在二進制時末尾0的個數,
或者說是i用2的冪方和表示時的最小指數。
( 當然,利用位運算,我們可以直接計算出2^k=i&(i^(i-1)) )
同時,我們也不難發現,這個k就是該節點在樹中的高度,因而這個樹的高度不會超過logn。
所以,當我們修改A[i]的值時,可以從C[i]往根節點一路上溯,調整這條路上的所有C[]即可,
這個操作的復雜度在最壞情況下就是樹的高度即O(logn)。
另外,對于求數列的前n項和,只需找到n以前的所有最大子樹,把其根節點的C加起來即可。
不難發現,這些子樹的數目是n在二進制時1的個數,或者說是把n展開成2的冪方和時的項數,
因此,求和操作的復雜度也是O(logn)。
接著,我們考察這兩種操作下標變化的規律:
首先看修改操作:
已知下標i,求其父節點的下標。
我們可以考慮對樹從邏輯上轉化:
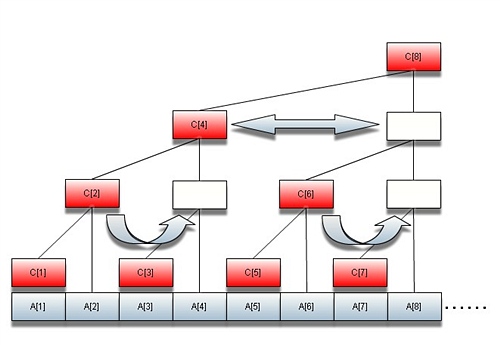
如圖,我們將子樹向右對稱翻折,虛擬出一些空白結點(圖中白色),將原樹轉化成完全二叉樹。
有圖可知,對于節點i,其父節點的下標與翻折出的空白節點下標相同。
因而父節點下標 p=i+2^k (2^k是i用2的冪方和展開式中的最小冪,即i為根節點子樹的規模)
即 p = i + i&(i^(i-1)) 。
接著對于求和操作:
因為每棵子樹覆蓋的范圍都是2的冪,所以我們要求子樹i的前一棵樹,只需讓i減去2的最小冪即可。
即 p = i - i&(i^(i-1)) 。
至此,我們已經比較詳細的分析了樹狀數組的復雜度和原理。
在最后,我們將給出一些樹狀數組的實現代碼,希望讀者能夠仔細體會其中的細節。
【代碼】
求最小冪2^k:
int Lowbit(int t)
{
return t & ( t ^ ( t - 1 ) );
}
|
求前n項和:
int Sum(int end)
{
int sum = 0;
while(end > 0)
{
sum += in[end];
end -= Lowbit(end);
}
return sum;
}
|
對某個元素進行加法操作:
void plus(int pos , int num)
{
while(pos <= n)
{
in[pos] += num;
pos += Lowbit(pos);
}
}