（本文假設讀者已經有以下知識：最短路徑的基本性質、Bellman-Ford算法。）
    比如有這樣一組不等式：
  
X1 - X2 <= 0
X1 - X5 <= -1
X2 - X5 <= 1
X3 - X1 <= 5
X4 - X1 <= 4
X4 - X3 <= -1
X5 - X3 <= -3
X5 - X4 <= -3
不等式組(1)

    全都是兩個未知數的差小于等于某個常數（大于等于也可以，因為左右乘以-1就可以化成小于等于）。這樣的不等式組就稱作差分約束系統。
    這個不等式組要么無解，要么就有無數組解。因為如果有一組解{X1, X2, ..., Xn}的話，那么對于任何一個常數k，{X1 + k, X2 + k, ..., Xn + k}肯定也是一組解，因為任何兩個數同時加一個數之后，它們的差是不變的，那么這個差分約束系統中的所有不等式都不會被破壞。
   
    差分約束系統的解法利用到了單源最短路徑問題中的三角形不等式。即對于任何一條邊u -> v，都有：

d(v) <= d(u) + w(u, v)

    其中d(u)和d(v)是從源點分別到點u和點v的最短路徑的權值，w(u, v)是邊u -> v的權值。
    顯然以上不等式就是d(v) - d(u) <= w(u, v)。這個形式正好和差分約束系統中的不等式形式相同。于是我們就可以把一個差分約束系統轉化成一張圖，每個未知數Xi對應圖中的一個頂點Vi，把所有不等式都化成圖中的一條邊。對于不等式Xi - Xj <= c，把它化成三角形不等式：Xi <= Xj + c，就可以化成邊Vj -> Vi，權值為c。最后，我們在這張圖上求一次單源最短路徑，這些三角形不等式就會全部都滿足了，因為它是最短路徑問題的基本性質嘛。
    話說回來，所謂單源最短路徑，當然要有一個源點，然后再求這個源點到其他所有點的最短路徑。那么源點在哪呢？我們不妨自已造一個。以上面的不等式組為例，我們就再新加一個未知數X0。然后對原來的每個未知數都對X0隨便加一個不等式（這個不等式當然也要和其它不等式形式相同，即兩個未知數的差小于等于某個常數）。我們索性就全都寫成Xn - X0 <= 0，于是這個差分約束系統中就多出了下列不等式：
   
X1 - X0 <= 0
X2 - X0 <= 0
X3 - X0 <= 0
X4 - X0 <= 0
X5 - X0 <= 0
不等式組(2)

    對于這5個不等式，也在圖中建出相應的邊。最后形成的圖如下： 
 

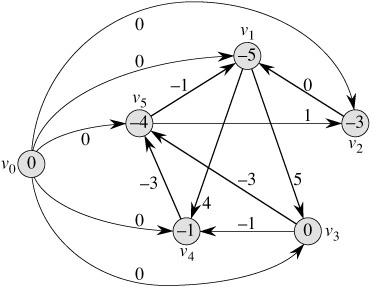
圖1

    圖中的每一條邊都代表差分約束系統中的一個不等式。現在以V0為源點，求單源最短路徑。最終得到的V0到Vn的最短路徑長度就是Xn的一個解啦。從圖1中可以看到，這組解是{-5, -3, 0, -1, -4}。當然把每個數都加上10也是一組解：{5, 7, 10, 9, 6}。但是這組解只滿足不等式組(1)，也就是原先的差分約束系統；而不滿足不等式組(2)，也就是我們后來加上去的那些不等式。當然這是無關緊要的，因為X0本來就是個局外人，是我們后來加上去的，滿不滿足與X0有關的不等式我們并不在乎。
    也有可能出現無解的情況，也就是從源點到某一個頂點不存在最短路徑。也說是圖中存在負權的圈。這一點我就不展開了，請自已參看最短路徑問題的一些基本定理。

    其實，對于圖1來說，它代表的一組解其實是{0, -5, -3, 0, -1, -4}，也就是說X0的值也在這組解當中。但是X0的值是無可爭議的，既然是以它作為源點求的最短路徑，那么源點到它的最短路徑長度當然是0了。因此，實際上我們解的這個差分約束系統無形中又存在一個條件：

X0 = 0

    也就是說在不等式組(1)、(2)組成的差分約束系統的前提下，再把其中的一個未知數的值定死。這樣的情況在實際問題中是很常見的。比如一個問題表面上給出了一些不等式，但還隱藏著一些不等式，比如所有未知數都大于等于0或者都不能超過某個上限之類的。比如上面的不等式組(2)就規定了所有未知數都小于等于0。
   
    對于這種有一個未知數定死的差分約束系統，還有一個有趣的性質，那就是通過最短路徑算法求出來的一組解當中，所有未知數都達到最大值。下面我來粗略地證明一下，這個證明過程要結合Bellman-Ford算法的過程來說明。
    假設X0是定死的；X1到Xn在滿足所有約束的情況下可以取到的最大值分別為M1、M2、……、Mn（當然我們不知道它們的值是多少）；解出的源點到每個點的最短路徑長度為D1、D2、……、Dn。
    基本的Bellman-Ford算法是一開始初始化D1到Dn都是無窮大。然后檢查所有的邊對應的三角形不等式，一但發現有不滿足三角形不等式的情況，則更新對應的D值。最后求出來的D1到Dn就是源點到每個點的最短路徑長度。
    如果我們一開始初始化D1、D2、……、Dn的值分別為M1、M2、……、Mn，則由于它們全都滿足三角形不等式（我們剛才已經假設M1到Mn是一組合法的解），則Bellman-Ford算法不會再更新任合D值，則最后得出的解就是M1、M2、……、Mn。
    好了，現在知道了，初始值無窮大時，算出來的是D1、D2、……、Dn；初始值比較小的時候算出來的則是M1、M2、……、Mn。大家用的是同樣的算法，同樣的計算過程，總不可能初始值大的算出來的結果反而小吧。所以D1、D2、……、Dn就是M1、M2、……、Mn。
   
    那么如果在一個未知數定死的情況下，要求其它所有未知數的最小值怎么辦？只要反過來求最長路徑就可以了。最長路徑中的三角不等式與最短路徑中相反：

d(v) >= d(u) + w(u, v)
也就是 d(v) - d(u) >= w(u, v)

    所以建圖的時候要先把所有不等式化成大于等于號的。其它各種過程，包括證明為什么解出的是最小值的證法，都完全類似。
   
    用到差分約束系統的題目有ZJU 2770