強烈推薦此題。此題應用樹型DP解答。
首先明確一點,題中的環至少需要3個頂點。因此,對于樹中的每個頂點,有3種狀態。
f[x][0]表示以x為根的樹,變成每個頂點恰好在一個環中的圖,需要連的最少邊數。
f[x][1]表示以x為根的樹,除了根x以外,其余頂點變成每個頂點恰好在一個環中的圖,需要連的最少邊數。
f[x][2]表示以x為根的樹,除了根x以及和根相連的一條鏈(算上根一共至少2個頂點)以外,其余頂點變成每個頂點恰好在一個環中的圖,需要連的最少邊數。
有四種狀態轉移(假設正在考慮的頂點是R,有k個兒子):
A.根R的所有子樹自己解決(取狀態0),轉移到R的狀態1。即R所有的兒子都變成每個頂點恰好在一個環中的圖,R自己不變。
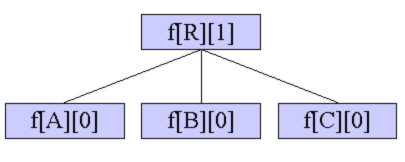
B.根R的k-1個棵樹自己解決,剩下一棵子樹取狀態1和狀態2的最小值,轉移到R的狀態2。剩下的那棵子樹和根R就構成了長度至少為2的一條鏈。
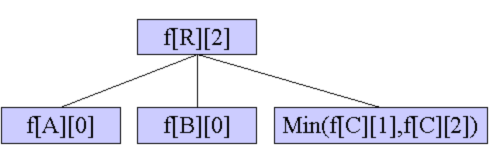
C.根R的k-2棵子樹自己解決,剩下兩棵子樹取狀態1和狀態2的最小值,在這兩棵子樹之間連一條邊,轉移到R的狀態0。
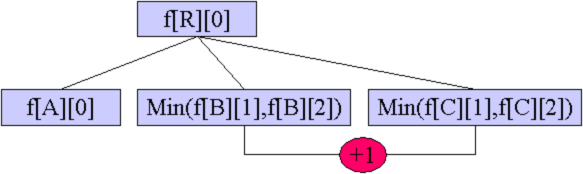
D.根R的k-1棵子樹自己解決,剩下一棵子樹取狀態2(子樹里還剩下長度至少為2的一條鏈),在這棵子樹和根之間連一條邊,構成一個環,轉移到R的狀態0。
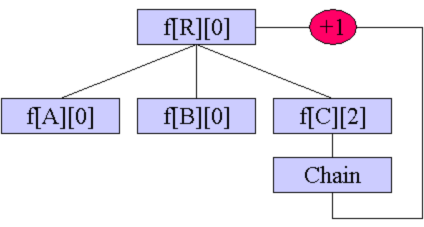
這樣就完成了樹型DP。

 /**//*************************************************************************
/**//*************************************************************************
 Author: WHU_GCC
Author: WHU_GCC
 Created Time: 2007-8-30 10:44:23
Created Time: 2007-8-30 10:44:23
 File Name: pku1848.cpp
File Name: pku1848.cpp
 Description:
Description:
 ************************************************************************/
************************************************************************/
 #include <iostream>
#include <iostream>
 #include <vector>
#include <vector>
 using namespace std;
using namespace std;
 #define out(x) (cout << #x << ": " << x << endl)
#define out(x) (cout << #x << ": " << x << endl)
 const int maxint = 0x7FFFFFFF;
const int maxint = 0x7FFFFFFF;
 typedef long long int64;
typedef long long int64;
 const int64 maxint64 = 0x7FFFFFFFFFFFFFFFLL;
const int64 maxint64 = 0x7FFFFFFFFFFFFFFFLL;

 template <class T> void show(T a, int n)
template <class T> void show(T a, int n)  {for (int i = 0; i < n; ++i) cout << a[i] << ' '; cout << endl; }
{for (int i = 0; i < n; ++i) cout << a[i] << ' '; cout << endl; }

 template <class T> void show(T a, int r, int l)
template <class T> void show(T a, int r, int l)  {for (int i = 0; i < r; ++i) show(a[i], l); cout << endl; }
{for (int i = 0; i < r; ++i) show(a[i], l); cout << endl; }

 const int maxn = 110;
const int maxn = 110;
 const int inf = 10000;
const int inf = 10000;

 int n;
int n;
 vector <int> v[maxn];
vector <int> v[maxn];
 int f[maxn][3];
int f[maxn][3];
 int used[maxn];
int used[maxn];

 void dfs(int now)
void dfs(int now)


 {
{
 used[now] = 1;
used[now] = 1;
 vector <int> child;
vector <int> child;
 for (int i = 0; i < v[now].size(); i++) if (!used[v[now][i]])
for (int i = 0; i < v[now].size(); i++) if (!used[v[now][i]])


 {
{
 dfs(v[now][i]);
dfs(v[now][i]);
 child.push_back(v[now][i]);
child.push_back(v[now][i]);
 }
}
 if (child.size() == 0)
if (child.size() == 0)


 {
{
 f[now][0] = inf;
f[now][0] = inf;
 f[now][1] = 0;
f[now][1] = 0;
 f[now][2] = inf;
f[now][2] = inf;
 }
}
 // case 1
// case 1


 {
{
 int sum = 0;
int sum = 0;
 for (int i = 0; i < child.size(); i++)
for (int i = 0; i < child.size(); i++)
 sum += f[child[i]][0];
sum += f[child[i]][0];
 f[now][1] <?= sum;
f[now][1] <?= sum;
 }
}
 // case 2
// case 2
 for (int i = 0; i < child.size(); i++)
for (int i = 0; i < child.size(); i++)


 {
{
 int p = min(f[child[i]][1], f[child[i]][2]);
int p = min(f[child[i]][1], f[child[i]][2]);
 int sum = 0;
int sum = 0;
 for (int j = 0; j < child.size(); j++) if (j != i)
for (int j = 0; j < child.size(); j++) if (j != i)
 sum += f[child[j]][0];
sum += f[child[j]][0];
 f[now][2] <?= sum + p;
f[now][2] <?= sum + p;
 f[now][0] <?= sum + f[child[i]][2] + 1;
f[now][0] <?= sum + f[child[i]][2] + 1;
 }
}
 // case 3
// case 3
 for (int i = 0; i < child.size(); i++)
for (int i = 0; i < child.size(); i++)
 for (int j = i + 1; j < child.size(); j++)
for (int j = i + 1; j < child.size(); j++)


 {
{
 int p1 = min(f[child[i]][1], f[child[i]][2]);
int p1 = min(f[child[i]][1], f[child[i]][2]);
 int p2 = min(f[child[j]][1], f[child[j]][2]);
int p2 = min(f[child[j]][1], f[child[j]][2]);
 int sum = 0;
int sum = 0;
 for (int k = 0; k < child.size(); k++) if (k != i && k != j)
for (int k = 0; k < child.size(); k++) if (k != i && k != j)
 sum += f[child[k]][0];
sum += f[child[k]][0];
 f[now][0] <?= sum + p1 + p2 + 1;
f[now][0] <?= sum + p1 + p2 + 1;
 }
}
 }
}

 int dp()
int dp()


 {
{
 for (int i = 1; i <= n; i++)
for (int i = 1; i <= n; i++)
 f[i][0] = f[i][1] = f[i][2] = inf;
f[i][0] = f[i][1] = f[i][2] = inf;
 memset(used, 0, sizeof(used));
memset(used, 0, sizeof(used));
 dfs(1);
dfs(1);
 if (f[1][0] == inf)
if (f[1][0] == inf)
 return -1;
return -1;
 return f[1][0];
return f[1][0];
 }
}

 int main()
int main()


 {
{
 while (scanf("%d", &n) != EOF)
while (scanf("%d", &n) != EOF)


 {
{
 for (int i = 0; i < n - 1; i++)
for (int i = 0; i < n - 1; i++)


 {
{
 int t1, t2;
int t1, t2;
 scanf("%d%d", &t1, &t2);
scanf("%d%d", &t1, &t2);
 v[t1].push_back(t2);
v[t1].push_back(t2);
 v[t2].push_back(t1);
v[t2].push_back(t1);
 }
}
 printf("%d\n", dp());
printf("%d\n", dp());
 }
}
 return 0;
return 0;
 }
}