在今年的信息學冬令營上,陳啟峰提出了一個自己創造的BST數據結構—Size Balanced Tree。這個平衡二叉樹被全世界內的許多網站所討論,大家討論的主題也只有一個—SBT能夠取代Treap嗎?本文詳細介紹SBT樹的性質,以及一些常用的操作,最后證明SBT是一顆高度平衡的二分查找樹。
一. 介紹
眾所周知,BST能夠快速的實現查找等動態操作。但是在某些情況下,比如將一個有序的序列依次插入到BST中,則BST會退化成為一條鏈,效率非常之低。由此引申出來很多平衡BST,比如AVL樹,紅黑樹,treap樹等。這些數據結構都是通過引入其他一些性質來保證BST的高度在最壞的情況下都保持在O(log n)。其中,AVL樹和紅黑樹的很多操作都非常麻煩,因此實際應用不是很多。而treap樹加入了一些隨機化堆的性質,實際應用效果非常好,實現起來很簡單,一直以來受到很多人的青睞。本文介紹一種新的平衡BST樹,實現起來也是非常之簡單,并且能夠支持更多的操作,實際評測效率跟treap也不差上下。
在介紹SBT之前,先介紹一下BST以及在BST上的旋轉操作。
1. Binary Search Tree
BST是一種高級的數據結構,它支持很多動態操作,包括查找,求最小值,最大值,前驅,后繼,插入和刪除,能夠用于字典以及優先隊列。
BST是一棵二叉樹,每個結點最多有2個兒子。每個結點都有個鍵值,并且鍵值必須滿足下面的條件:
如果x是BST中的一個結點。那么x的鍵值不小于其左兒子的鍵值,并且不大于其右兒子的鍵值。
對于每個結點t,用left[t]和right[t]分別來存放它的兩個兒子,ket[t]存放該結點的鍵值。另外,在SBT中,要增加s[t],用來保存以t為根的子樹中結點的個數。
2. 旋轉
為了保證BST的平衡(不會退化成為一條鏈),通常通過旋轉操作來改變BST的結構。旋轉操作不會影響binary-search-tree的性質!

2.1右旋操作的偽代碼
右旋操作必須保證左兒子存在
Right-Rotate(t)
k←left[t]
left[t]←right[k]
right[k]←t
s[k]←s[t]
s[t]←s[left[t]]+s[right[t]]+1
t←k
2.2 左旋操作的偽代碼
左旋操作必須保證右兒子存在
Left-Rotate(t)
k←right[t]
right[t]←left[k]
left[k]←t
s[k]←s[t]
s[t]←s[left[t]]+s[right[t]]+1
t←k
二.Size Balanced Tree
Size Balanced Tree(簡稱SBT)是一種平衡二叉搜索樹,它通過子樹的大小s[t]來維持平衡性質。它支持很多動態操作,并且都能夠在O(log n)的時間內完成。
|
Insert(t,v)
|
將鍵值為v的結點插入到根為t的樹中
|
|
Delete(t,v)
|
在根為t的樹中刪除鍵值為v的結點
|
|
Find(t,v)
|
在根為t的樹中查找鍵值為v的結點
|
|
Rank(t,v)
|
返回根為t的樹中鍵值v的排名。也就是樹中鍵值比v小的結點數+1
|
|
Select(t,k)
|
返回根為t的樹中排名為k的結點。同時該操作能夠實現Get-min,Get-max,因為Get-min等于Select(t,1),Get-max等于Select(t,s[t])
|
|
Pred(t,v)
|
返回根為t的樹中比v小的最大的鍵值
|
|
Succ(t,v)
|
返回根為t的樹中比v大的最小的鍵值
|
SBT樹中的每個結點都有left,right,key以及前面提到的size域。SBT能夠保持平衡性質是因為其必須滿足下面兩個條件:
對于SBT中的每個結點t,有性質(a)(b):
(a). s[right[t]]≥s[left[left[t]]],s[right[left[t]]]
(b). s[left[t]]≥s[right[right[t]]],s[left[right[t]]]

即在上圖中,有s[A],s[B]≤s[R]&s[C],s[D] ≤s[L]
三. Maintain
假設我們要在BST中插入一個鍵值為v的結點,一般是用下面這個過程:
Simple-Insert(t,v)
If t=0 then
t←NEW-NODE(v)
Else
s[t]←s[t]+1
If v<key[t] then
Simple-Insert(left[t],v)
Else
Simple-Insert(right[t],v)
執行完操作Simple-Insert后,SBT的性質(a)和(b)就有可能不滿足了,這是我們就需要修復(Maintain)SBT。
Maintain(t)用來修復根為t的SBT,使其滿足SBT性質。由于性質(a)和(b)是對稱的,下面僅討論對性質(a)的修復。
Case 1:s[left[left[t]]]>s[right[t]]

這種情況下可以執行下面的操作來修復SBT
執行Right-Rotate(T)
有可能旋轉后的樹仍然不是SBT,需要再次執行Maintain(T)
由于L的右兒子發生了變化,因此需要執行Maintain(L)
Case 2:s[right[left[t]]]>s[right[t]]
這種情況如下圖所示:

需要執行一下步驟來修復SBT:
執行Left-Rotate(L)。如下圖所示

執行Right-Rotate(T)。如下圖所示

當執行完(1)(2)后,樹的結構變得不可預測了。但是幸運的是,在上圖中,A,E,F,R子樹仍然是SBT。因此我們可以執行Maintain(L)和Maintain(T)來修復B的子樹。
Case 3:
這種情況和case 1是對稱的
Case 4:
這種情況和case 2是對稱的
Maintain操作的偽代碼:
在Maintain過程中,用一個變量flag來避免額外的檢查。當flag為false時,代表case 1和case 2需要被檢查,否則case 3和case 4需要被檢查。
Maintain (t,flag)
If flag=false then
If s[left[left[t]]>s[right[t]] then
Right-Rotate(t)
Elseif s[right[left[t]]>s[right[t]] then
Left-Rotate(left[t])
Right-Rotate(t)
Else exit
Elseif s[right[right[t]]>s[left[t]] then
Left-Rotate(t)
Elseif s[left[right[t]]>s[left[t]] then
Right-Rotate(right[t])
Left-Rotate(t)
Else exit
Maintain(left[t],false)
Maintain(right[t],true)
Maintain(t,false)
Maintain(t,true)
四.常用操作
插入操作
SBT和插入操作和BST的基本相同,只是在插入之后需要執行下Maintain操作。
Insert (t,v)
If t=0 then
t←NEW-NODE(v)
Else
s[t] ←s[t]+1
If v<key[t] then
Simple-Insert(left[t],v)
Else
Simple-Insert(right[t],v)
Maintain(t,v≥key[t])
刪除操作
如果沒有找到要刪除的結點,那么就刪除最后一個訪問的結點并記錄。
Delete (t,v)
If s[t]≤2 then
record←key[t]
t←left[t]+right[t]
Exit
s[t] ←s[t]-1
If v=key[t] then
Delete(left[t],v[t]+1)
Key[t] ←record
Maintain(t,true)
Else
If v<key[t] then
Delete(left[t],v)
Else
Delete(right[t],v)
Maintain(t,v<key[t])
另外,由于SBT的平衡性質是靠size域來維護的,而size域本身(子樹所含節點個數)對于很多查詢算法都特別有用,這樣使得查詢集合里面的譬如第n小的元素,以及一個元素在集合中的排名等操作都異常簡單,并且時間復雜度都穩定在O(log n)。下面僅介紹下上表提到的select(t,k)操作和rank(t,v)操作。
由于SBT的性質(結點t的關鍵字比其左子樹中所有結點的關鍵字都大,比其左子樹中所有的關鍵字都小),理解下面的算法非常容易。
3.Select操作
Select(t,k)
If k=s[left[t]]+1 then
return key[t]
If k<=s[left[t]] then
return Select(left[t],k)
Else
return Select(right[t],k-1-s[left[t]])
4.Rank操作
Rank(t,v)
If t=0 then
return 1
If v<=key[t] then
return rank(left[t],v)
Else
return s[left[t]]+1+rank(right[t],v)
同樣,求前驅結點的操作Pred和后繼結點的操作都很容易通過size域來實現。
五.相關證明分析
顯然Maintain操作是一個遞歸過程,可能你會懷疑它是否會結束。下面我們可以證明Maintain操作的平攤時間復雜度為O(1)。
1.關于樹的高度的分析
設f[h]表示高度為h的SBT中結點數目的最小值,則有
1 (h=0)
f[h]= 2 (h=1)
f[h-1]+f[h-2]+1 (h>1)
a.證明:
(1) 很明顯f[0]=1,f[1]=2。
(2) 首先,對于任意h>1,我們假設t是一顆高度為h的SBT的根結點,則這顆SBT包含一顆高度為h-1的子樹。不妨假設t的左子樹的高度為h-1,根據f[h]的定義,有
s[left[t] ]≥f[h-1],同樣的,左子樹中有一顆高度為h-2的子樹,換句話說,左子樹中含有一顆結點數至少為f[h-2]的子樹。由SBT的性質(b),可知s[right[t]] ≥f[h-2]。因此我們有s[t]=s[left[t]]+s[right[t]]+1≥f[h-1]+f[h-2]+1。
另外一方面,我們可以構造一顆高度為h,并且結點數正好為f[h]的SBT,稱這樣的SBT為tree[t]。可以這樣來構造tree[h]:
含有一個結點的SBT (h=0)
tree[h]= 含有2個結點的任意SBT (h=1)
左子樹為tree[h-1],右子樹為tree[h-2]的SBT (h>1)
由f[h]的定義可知f[h] ≤f[h-1]+f[h-2]+1(h>1)。因此f[h]的上下界都為f[h-1]+f[h-2]+1,因此有f[h]=f[h-1]+f[h-2]+1。
b.最壞情況下的高度
事實上f[h]是一個指數函數,通過f[h]的遞推可以計算出通項公式。

定理:
含有n個結點的SBT在最壞情況下的高度是滿足f[h] ≤n的最大的h值。
假設maxh為含有n個結點的SBT的最壞情況下的高度。由上面的定理,有
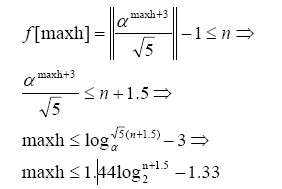
于是很明顯SBT的高度為O(logn),是一顆高度平衡的BST!
2.對Maintain操作的分析
通過前面的計算分析我們能夠很容易分析出Maintain操作是非常高效的。
首先,有一個非常重要的值來評價一顆BST的好壞:所有結點的平均深度。它是通過所有結點的深度之和SD除以結點個數n計算出來的。一般來說,這個值越小,這顆BST就越好。由于對于一顆BST來說,結點數n是一個常數,因此我們期望SD值越小越好。
現在我們集中來看SBT的SD值,它的重要性在于能夠制約Maintain操作的執行時間。回顧先前提到的BST中的旋轉操作,有個重要的性質就是:每次執行旋轉操作后,SD值總是遞減的!
由于SBT樹的高度總是O(log n),因此SD值也總是保持在O(log n)。并且SD僅在插入一個結點到SBT后才增加,因此(T是Maintain操作中執行旋轉的次數)

Maintain操作的次數等于T加上不需要旋轉操作的Maintain操作的次數。由于后者為O(nlogn)+O(T),因此Maintain的平攤分析時間復雜度為:

對各個操作時間復雜度的分析
現在我們知道了SBT的高度為O(log n),并且 Maintain操作的平攤分析時間復雜度為O(1),因此對于所有的常用操作,時間復雜度都穩定在O(log n)!