卡塔蘭數(shù)
catalan數(shù)的表達(dá)形式
h(n) = C(2n,n)/(n+1) （n>=0）
h(n) = C(2n-2,n-1)/n (n>=1)
對(duì)catalan數(shù)的應(yīng)用(形式類似，關(guān)鍵是能否對(duì)問題建模了)
1.括號(hào)化問題。
矩陣鏈乘： P=A1×A2×A3×……×An，依據(jù)乘法結(jié)合律，不改變其順序，只用括號(hào)表示成對(duì)的乘積，試問有幾種括號(hào)化的方案？
分析：可以將分割看成構(gòu)成二叉樹的情形。
2.將多邊行劃分為三角形問題。將一個(gè)凸多邊形區(qū)域分成三角形區(qū)域(劃分線不交叉)的方法數(shù)?
類似：在圓上選擇2n個(gè)點(diǎn),將這些點(diǎn)成對(duì)連接起來使得所得到的n條線段不相交的方法數(shù)?
分析：同矩陣鏈乘。
3.出棧次序問題。一個(gè)棧(無窮大)的進(jìn)棧序列為1,2,3,..n,有多少個(gè)不同的出棧序列?
類似：有2n個(gè)人排成一行進(jìn)入劇場(chǎng)。入場(chǎng)費(fèi)5元。其中只有n個(gè)人有一張5元鈔票，另外n人只有10元鈔票，劇院無其它鈔票，問有多少中方法使得只要有10元的人買票，售票處就有5元的鈔票找零？(將持5元者到達(dá)視作將5元入棧，持10元者到達(dá)視作使棧中某5元出棧)
類似：一位大城市的律師在他住所以北n個(gè)街區(qū)和以東n個(gè)街區(qū)處工作。每天她走2n個(gè)街區(qū)去上班。如果他從不穿越（但可以碰到）從家到辦公室的對(duì)角線，那么有多少條可能的道路？
分析：對(duì)于每一個(gè)數(shù)來說，必須進(jìn)棧一次、出棧一次。我們把進(jìn)棧設(shè)為狀態(tài)‘1’，出棧設(shè)為狀態(tài)‘0’。n個(gè)數(shù)的所有狀態(tài)對(duì)應(yīng)n個(gè)1和n個(gè)0組成的2n位二進(jìn)制數(shù)。由于等待入棧的操作數(shù)按照1‥n的順序排列、入棧的操作數(shù)b大于等于出棧的操作數(shù)a(a≤b)，因此輸出序列的總數(shù)目=由左而右掃描由n個(gè)1和n個(gè)0組成的2n位二進(jìn)制數(shù)，1的累計(jì)數(shù)不小于0的累計(jì)數(shù)的方案種數(shù)。 在2n位二進(jìn)制數(shù)中填入n個(gè)1的方案數(shù)為c(2n,n),不填1的其余n位自動(dòng)填0。從中減去不符合要求（由左而右掃描，0的累計(jì)數(shù)大于1的累計(jì)數(shù)）的方案數(shù)即為所求。
不符合要求的數(shù)的特征是由左而右掃描時(shí)，必然在某一奇數(shù)位2m+1位上首先出現(xiàn)m+1個(gè)0的累計(jì)數(shù)和m個(gè)1的累計(jì)數(shù)，此后的2(n-m)-1位上有n-m個(gè) 1和n-m-1個(gè)0。如若把后面這2(n-m)-1位上的0和1互換，使之成為n-m個(gè)0和n-m-1個(gè)1，結(jié)果得1個(gè)由n+1個(gè)0和n-1個(gè)1組成的2n位數(shù)，即一個(gè)不合要求的數(shù)對(duì)應(yīng)于一個(gè)由n+1個(gè)0和n-1個(gè)1組成的排列。
反過來，任何一個(gè)由n+1個(gè)0和n-1個(gè)1組成的2n位二進(jìn)制數(shù)，由于0的個(gè)數(shù)多2個(gè)，2n為偶數(shù)，故必在某一個(gè)奇數(shù)位上出現(xiàn)0的累計(jì)數(shù)超過1的累計(jì)數(shù)。同樣在后面部分0和1互換，使之成為由n個(gè)0和n個(gè)1組成的2n位數(shù)，即n+1個(gè)0和n-1個(gè)1組成的2n位數(shù)必對(duì)應(yīng)一個(gè)不符合要求的數(shù)。
因而不合要求的2n位數(shù)與n＋1個(gè)0，n－1個(gè)1組成的排列一一對(duì)應(yīng)。
顯然，不符合要求的方案數(shù)為c(2n,n+1)。由此得出 輸出序列的總數(shù)目=c(2n,n)-c(2n,n+1)=1/(n+1)*c(2n,n).（這個(gè)公式的下標(biāo)是從h(0)=1開始的）
4.給定N個(gè)節(jié)點(diǎn)，能構(gòu)成多少種形狀不同的二叉樹？
分析：先去一個(gè)點(diǎn)作為頂點(diǎn),然后左邊依次可以取0至N-1個(gè)相對(duì)應(yīng)的,右邊是N-1到0個(gè),兩兩配對(duì)相乘,就是h(0)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(0)=h(n))
參考：
卡塔蘭數(shù)是組合數(shù)學(xué)中一個(gè)常出現(xiàn)在各種計(jì)數(shù)問題中出現(xiàn)的數(shù)列。由以比利時(shí)的數(shù)學(xué)家歐仁·查理·卡塔蘭 (1814–1894)命名。
卡塔蘭數(shù)的一般項(xiàng)公式為 
另類遞歸式： h(n)=((4*n-2)/(n+1))*h(n-1);
前幾項(xiàng)為 （OEIS中的數(shù)列A000108）: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
[編輯]性質(zhì)
Cn的另一個(gè)表達(dá)形式為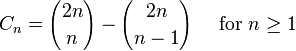
所以，Cn是一個(gè)自然數(shù)；這一點(diǎn)在先前的通項(xiàng)公式中并不顯而易見。這個(gè)表達(dá)形式也是André對(duì)前一公式證明的基礎(chǔ)。(見下文的第二個(gè)證明。)
卡塔蘭數(shù)滿足以下遞推關(guān)系
它也滿足
這提供了一個(gè)更快速的方法來計(jì)算卡塔蘭數(shù)。
卡塔蘭數(shù)的漸近增長(zhǎng)為
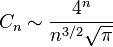
它的含義是左式除以右式的商趨向于1當(dāng)n → ∞。（這可以用n!的斯特靈公式來證明。）
所有的奇卡塔蘭數(shù)Cn都滿足n = 2k − 1。所有其他的卡塔蘭數(shù)都是偶數(shù)。
[編輯]應(yīng)用
組合數(shù)學(xué)中有非常多.的組合結(jié)構(gòu)可以用卡塔蘭數(shù)來計(jì)數(shù)。在Richard P. Stanley的Enumerative Combinatorics: Volume 2一書的習(xí)題中包括了66個(gè)相異的可由卡塔蘭數(shù)表達(dá)的組合結(jié)構(gòu)。以下用Cn=3和Cn=4舉若干例：
- Cn表示長(zhǎng)度2n的dyck word的個(gè)數(shù)。Dyck word是一個(gè)有n個(gè)X和n個(gè)Y組成的字串，且所有的部分字串皆滿足X的個(gè)數(shù)大于等于Y的個(gè)數(shù)。以下為長(zhǎng)度為6的dyck words:
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
- 將上例的X換成左括號(hào)，Y換成右括號(hào)，Cn表示所有包含n組括號(hào)的合法運(yùn)算式的個(gè)數(shù):
((())) ()(()) ()()() (())() (()())
- Cn表示有n+1個(gè)葉子的二叉樹的個(gè)數(shù)。
- Cn表示所有不同構(gòu)的含n個(gè)分枝結(jié)點(diǎn)的滿二叉樹的個(gè)數(shù)。（一個(gè)有根二叉樹是滿的當(dāng)且僅當(dāng)每個(gè)結(jié)點(diǎn)都有兩個(gè)子樹或沒有子樹。）
證明：
令1表示進(jìn)棧，0表示出棧，則可轉(zhuǎn)化為求一個(gè)2n位、含n個(gè)1、n個(gè)0的二進(jìn)制數(shù)，滿足從左往右掃描到任意一位時(shí)，經(jīng)過的0數(shù)不多于1數(shù)。顯然含n個(gè)1、n個(gè)0的2n位二進(jìn)制數(shù)共有
個(gè)，下面考慮不滿足要求的數(shù)目.
考慮一個(gè)含n個(gè)1、n個(gè)0的2n位二進(jìn)制數(shù)，掃描到第2m+1位上時(shí)有m+1個(gè)0和m個(gè)1（容易證明一定存在這樣的情況），則后面的0-1排列中必有n-m個(gè)1和n-m-1個(gè)0。將2m+2及其以后的部分0變成1、1變成0，則對(duì)應(yīng)一個(gè)n+1個(gè)0和n-1個(gè)1的二進(jìn)制數(shù)。反之亦然（相似的思路證明兩者一一對(duì)應(yīng)）。
從而
。證畢。
- Cn表示所有在n × n格點(diǎn)中不越過對(duì)角線的單調(diào)路徑的個(gè)數(shù)。一個(gè)單調(diào)路徑從格點(diǎn)左下角出發(fā)，在格點(diǎn)右上角結(jié)束，每一步均為向上或向右。計(jì)算這種路徑的個(gè)數(shù)等價(jià)于計(jì)算Dyck word的個(gè)數(shù)： X代表“向右”，Y代表“向上”。下圖為n = 4的情況：
-
- Cn表示通過連結(jié)頂點(diǎn)而將n + 2邊的凸多邊形分成三角形的方法個(gè)數(shù)。下圖中為n = 4的情況：
- Cn表示對(duì){1, ..., n}依序進(jìn)出棧的置換個(gè)數(shù)。一個(gè)置換w是依序進(jìn)出棧的當(dāng)S(w) = (1, ..., n), 其中S(w)遞歸定義如下：令w = unv，其中n為w的最大元素，u和v為更短的數(shù)列；再令S(w) =S(u)S(v)n，其中S為所有含一個(gè)元素的數(shù)列的單位元。
- Cn表示用n個(gè)長(zhǎng)方形填充一個(gè)高度為n的階梯狀圖形的方法個(gè)數(shù)。下圖為 n = 4的情況:
百度百科資料:
簡(jiǎn)介
中文:卡特蘭數(shù)
Catalan數(shù)是組合數(shù)學(xué)中一個(gè)常出現(xiàn)在各種計(jì)數(shù)問題中出現(xiàn)的數(shù)列。由以比利時(shí)的數(shù)學(xué)家歐仁·查理·卡塔蘭 (
1814–1894)命名。
原理：
令h(0)=1,h(1)＝1,catalan數(shù)滿足遞歸式：
h(n)= h(0)*h(n-1) + h(1)*h(n-2) + 
+ h(n-1)h(0) (其中n>=2)
該遞推關(guān)系的解為：
h(n)=C(2n,n)/(n + 1) (n=1,2,3,)
另類遞歸式： h(n)=((4*n-2)/(n+1))*h(n-1);
前幾項(xiàng)為 （OEIS中的數(shù)列A000108）: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452,
應(yīng)用
我總結(jié)了一下，最典型的四類應(yīng)用：（實(shí)質(zhì)上卻都一樣，無非是遞歸等式的應(yīng)用，就看你能不能分解問題寫出遞歸式了）
1.括號(hào)化問題。
矩陣鏈乘： P=a1×a2×a3×……×an，依據(jù)乘法結(jié)合律，不改變其順序，只用括號(hào)表示成對(duì)的乘積，試問有幾種括號(hào)化的方案？(h(n)種)
2.出棧次序問題。
一個(gè)棧(無窮大)的進(jìn)棧序列為1,2,3,..n,有多少個(gè)不同的出棧序列?
類似：
(1)有2n個(gè)人排成一行進(jìn)入劇場(chǎng)。入場(chǎng)費(fèi)5元。其中只有n個(gè)人有一張5元鈔票，另外n人只有10元鈔票，劇院無其它鈔票，問有多少中方法使得只要有10元的人買票，售票處就有5元的鈔票找零？(將持5元者到達(dá)視作將5元入棧，持10元者到達(dá)視作使棧中某5元出棧)
(2)在圓上選擇2n個(gè)點(diǎn),將這些點(diǎn)成對(duì)連接起來，使得所得到的n條線段不相交的方法數(shù)。
3.將多邊行劃分為三角形問題。
將一個(gè)凸多邊形區(qū)域分成三角形區(qū)域的方法數(shù)?
類似：一位大城市的律師在她住所以北n個(gè)街區(qū)和以東n個(gè)街區(qū)處工作。每天她走2n個(gè)街區(qū)去上班。如果她
從不穿越（但可以碰到）從家到辦公室的對(duì)角線，那么有多少條可能的道路？
類似：在圓上選擇2n個(gè)點(diǎn),將這些點(diǎn)成對(duì)連接起來使得所得到的n條線段不相交的方法數(shù)?
4.給頂節(jié)點(diǎn)組成二叉樹的問題。
給定N個(gè)節(jié)點(diǎn)，能構(gòu)成多少種形狀不同的二叉樹？
(一定是二叉樹!
先去一個(gè)點(diǎn)作為頂點(diǎn),然后左邊依次可以取0至N-1個(gè)相對(duì)應(yīng)的,右邊是N-1到0個(gè),兩兩配對(duì)相乘,就是h(0)*h(n-1) + h(2)*h(n-2) + + h(n-1)h(0)=h(n))
（能構(gòu)成h（N）個(gè)）