轉(zhuǎn)載文章一：http://www.cnblogs.com/shanhaobo/articles/1065380.html

[3D基礎(chǔ)]理解計算機3D圖形學中的坐標系變換

     要談坐標系變換，那么坐標系有哪些呢？依次有:物體坐標系，世界坐標系，相機坐標系，投影坐標系以及屏幕坐標系.我要討論的就是這些坐標系間的轉(zhuǎn)換。
     這些坐標系不是憑空而來，他們都是為了完成計算機3D圖形學最最最基本的目標而出現(xiàn).
      計算機3D圖形學最最最基本的目標就是:將構(gòu)建好的3D物體顯示在2D屏幕坐標上.
      初看好像就是將最初的物體坐標系轉(zhuǎn)換到屏幕坐標系就可以了呀，為什么多出了世界坐標系,相機坐標系，投影坐標 系。這是因為:在一個大世界里有多個物體，而每個物體都有自己的坐標系，如何表述這些物體間相對的關(guān)系，這個多出了世界坐標系；如果只需要看到這個世界其 中一部分，這里就多出了相機坐標系；至于投影坐標系那是因為直接將3D坐標轉(zhuǎn)換為屏幕坐標是非常復(fù)雜的(因為它們不僅維度不同,度量不同（屏幕坐標一般都 是像素為單位,3D空間中我們可以現(xiàn)實世界的米，厘米為單位），XY的方向也不同，在2D空間時還要進行坐標系變換),所以先將3D坐標降維到2D坐標, 然后2D坐標轉(zhuǎn)換到屏幕坐標。
理解3D圖形學的第一步:理解左手坐標系與右手坐標系
      為什么會有左手坐標系與右手坐標系之分？
      在3D空間(沒錯！就是3D)中，所有2D坐標系是等價的（就是通過一系列的仿射變換，可以互相轉(zhuǎn)換）
      而3D坐標系不是等價的，通過仿射變換，是無法將左手坐標系轉(zhuǎn)換到右手坐標系；也就是說，物體坐標系用的就是左手坐標系，世界坐標系用的是右手 坐標系，那么物體可能就是不會是我們所希望的樣子了，可能是倒立的，也可能是背對著我們的，所以我們要區(qū)分左手坐標系與右手坐標系。也許在4D空間，左右 手坐標系就可以互相變換了吧。
      進入正題吧:
     首先討論的是物體坐標系->世界坐標系
      前面說了為了描述多個物體間相對的關(guān)系，這里引進了世界坐標系,所以世界坐標系是個參考坐標系。
      這一步的目的將所有的物體的點都轉(zhuǎn)移到世界坐標系，這里主要涉及的是旋轉(zhuǎn)，縮放，平移等。
      不過我將詳細說明為何及如何用矩陣來描述這些變換。
      例:如果有兩個坐標系C與C`, C`是C繞Z軸旋轉(zhuǎn)θ得到的。下面是各坐標軸的變換：
             
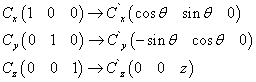
     如果是C坐標系的點P（x, y, z），而在C`的表示就是
   
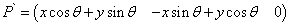
     這時該如何建立矩陣呢? 答案就是區(qū)分你用的是行向量還是列向量.也許有人會問為什么不區(qū)分是左手坐標系還是右手坐標系呢？因為C可以變換到C`,那么他們一定是同在左手坐標系或右手坐標系,變換只能在可以互相轉(zhuǎn)換的坐標系之間進行。
      如果你用的是行向量：由于行向量只能左乘矩陣(注意乘與乘以的區(qū)別)
      所以矩陣形式應(yīng)該是這樣
    
     只有這樣，在左乘矩陣時才能得到上面P`的形式。
    
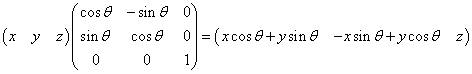
     如果你用的是列向量: 由于列向量只能右乘矩陣(注意乘與乘以的區(qū)別)
     所以矩陣形式應(yīng)該是這樣
    
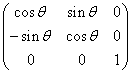
     只有這樣，在右乘矩陣時才能得到上面P`的形式。
  
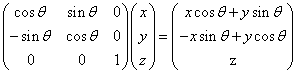
     至于如何旋轉(zhuǎn)，縮放，平移我不在多說。
     …………………………………覺得自己好像跑題了.還好這兩個坐標系變換很簡單。
     我們再討論世界坐標系->相機坐標系
     引進相機的目的就是只需看到世界的一部分，而哪些是可以在相機里看到的，就需要進行篩選。將物體轉(zhuǎn)換到相機坐標系，這樣相機坐標系進行篩選時就會簡單很多。這里的重點是構(gòu)建相機坐標系。
     物體坐標系，世界坐標系是美工在繪制時就定義好了的。而相機坐標系是需要程序?qū)崟r構(gòu)建的。（當然這是通常情況下，如果你要建立一個世界，這個世界都是圍繞 你轉(zhuǎn)，要實時改變所有物體坐標系，固定相機坐標系（其實這時候相機坐標系就是世界坐標系），建立一個地心說的世界，我也沒辦法，你的思維也太不一樣了。）
     如何構(gòu)建相機坐標系呢？首先我們要明確目標：我們是要構(gòu)建3D坐標系(好像是廢話)，三個坐標軸要互相垂直(也好像是廢話).
      我們一般用UVN相機。例如:D3D的D3DXMatrixLookAtLH，D3DXMatrixLookAtRH，OGL的gluLookAt(右手坐標系).
      如何建立呢UVN相機呢? 我們就要利用叉積這個工具了：兩個不平行，不重疊的向量的叉積可以得到與這兩個向量互相垂直的向量。
      如果有了相機的位置與目標的位置那么我們可以確定一個Z軸（有人問為什么是Z軸，因為物體的遠與近我們就習慣用Z值來表示的）。求Z軸時要注意 是左手坐標系還是右手坐標系，左右手坐標系XY軸方向相同時，Z軸的方向相反。所以左手坐標系是目標位置減去相機位置，而右手坐標系則是相機位置減去目標 位置。記得normalize
     這是我們要得到X與Y軸了。如何求X，Y軸呢？
     一般方法是：
     1、選擇一個臨時Y軸，
     2、對臨時Y 與Z 軸進行叉積求得一個X軸
     3、X軸再與Z軸進行叉積，得到一個Y軸。
     有了XYZ就可以求出旋轉(zhuǎn)的相機矩陣了。
     如何選擇一個Y軸呢？大多數(shù)情況下是（0，1，0），但是如果是相機位置E與目標位置T垂直,即（E-T=（0，+/-1，0）時），這時就不能用(0,1,0)了， 因為兩個平行向量的叉積是零向量，所以我們就要另選一個Y軸。
     但是我覺得我們可以改變方法。
      如果不能選Y軸，我們就選擇一個臨時X軸，這個臨時Ｘ軸就是（1，0，0）。
     然后再對臨時X軸與Z軸進行叉積求得一個Y軸。
     最后Y軸再與Z軸進行叉積，得到X軸。
      這樣可以得到XYZ軸。
      最后再根據(jù)行向量與列向量建立相機矩陣，再進行平移。

     相機坐標系->投影坐標系.
     投影的目的就是：降維.
      兩種投影方式：正交投影與透視投影.
      在我們TEAM中易穎已經(jīng)寫了，我就不多說了，大家去看他的文章。

     投影坐標系->屏幕坐標系
      這是最簡單的。2D坐標變換。也不多說。

轉(zhuǎn)載文章2：http://www.xingousi.com/computer/computergraphics.htm

計算機圖形學筆記(Part 1 )：計算機圖形學透視投影變換原理及一點和兩點透視

一、平行互分法

吳英凡所寫的《透視作圖的新方法——交點法體系》，其中談到的平行互分法，還是有道理的。

其實簡單點說，就是透視圖上的兩條“原來空間中的平行線”（在畫面上透視投影為相交于滅點），通過其中一條透視投影直線的端點畫另一條透視投影直線的平行線，必平行于畫面；這第三條線在畫面的透視投影的滅點必然在另一條透視投影線上。

二、透視投影變換學習總結(jié)

1、用多維數(shù)列表示低維空間坐標,加深理解齊次坐標表示法。

    齊次坐標表示法可以方便地運算，同時形狀不變。[x,y,z,0]表示一個無窮的點。

2、透視投影變換公式可以看成兩個矩陣的乘積，其中一個做透視變換，另外一個作正投影

   保留的z'值的確切含義：指的是在完全作完透視投影變換之前，僅作透視投影之后的一條線.

   它的幾何意義見李建平《計算機圖形學原理教程》第44頁。

3、左手和右手坐標系的坐標轉(zhuǎn)換

   “視點坐標系與一般的物體所在的世界坐標系不同，它遵循左手法則，即左手大拇指指向Z正軸，與之垂直的四個手指指向X正軸，四指彎曲90度的方向是Y正軸。而世界坐標系遵循右手法則的。”

4、視點坐標系的透視變換公式很重要！！王飛著計算機圖形學書65頁

5、z'值的確切含義：指的是在完全作完透視投影變換之前，僅作透視投影之后的一條線

三、兩點透視的變換矩陣：

王飛編著《計算機圖形學基礎(chǔ)》的道理是：

從平面圖形的平移、旋轉(zhuǎn)、錯切開始推導(dǎo)，兩點透視的變換矩陣可以看成是：

物體本身有一個物體坐標系——xw,yw,zw，視點作為原點又構(gòu)成一個視點坐標系——xe，ye，ze，物體坐標系z軸朝上，y軸朝向遠處；而視點坐標系y軸朝上，z軸朝向遠處。

這樣，最終的二點透視狀態(tài)可以這樣取得，首先把物體的位置的物體坐標系表示法轉(zhuǎn)化為視點坐標系的表示法（第一個矩陣），然后圍繞視點坐標系的y軸旋轉(zhuǎn)（第二個矩陣），然后在x，y，z方向上平移（第三個矩陣），最后做透視變換（第四個矩陣），它的原文是把平移放在第二步，我在平移之前轉(zhuǎn)動，目的是保證了物體旋轉(zhuǎn)的軸在離它不遠的地方：

我使用的矩陣變換如下，原文是是把平移放在第二步：

[xw,yw,zw,1]* ***

最后所得結(jié)果是一個新的矩陣，

[xe ye ze 1]=[cos*xw-sin*yw+l   zw+m   2sin*xw+2cos*yw+2n-d   (sin*xw+cos*yw+n）/d]

把最后一項變成1，可得

=[(cos*xw-sin*yw+l)*d/(sin*xw+cos*yw+n   (zw+m)*d/(sin*xw+cos*yw+n)   （2sin*xw+2cos*yw+2n-d）*d/(sin*xw+cos*yw+n)    1 ]

即：

Xe= (cos*xw-sin*yw+l)*d/(sin*xw+cos*yw+n)

Ye=(zw+m)*d/(sin*xw+cos*yw+n)

Ze=(2sin*xw+2cos*yw+2*n-d)*d/(sin*xw+cos*yw+n)

實際上我的delphi程序里面是這樣的：

xe:=trunc((cos(angle)*eee[ii][k].X-sin(angle)*eee[ii][k].Y+l)*d/(sin(angle)*eee[ii][k].X+cos(angle)*eee[ii][k].Y+n));

        ye:=trunc((hhh[ii][k]+m)*d/(sin(angle)*eee[ii][k].X+cos(angle)*eee[ii][k].Y+n)); //透視變換

        //ze可以考慮使用作為消隱

Ze:=trunc((2*sin(angle)*xw+2*cos(angle)*yw+2*n-d)*d/(sin(angle)*xw+cos(angle)*yw+n));

四、通過變換過的兩點透視的結(jié)果xe,ye，zw和*，反求原來的物體坐標xw,yw

即：xe,ye，zw和已知，求出xw,yw

根據(jù)：

Xe= (cos*xw-sin*yw+l)*d/(sin*xw+cos*yw+n)          （1）

Ye=(zw+m)*d/(sin*xw+cos*yw+n)                         （2）

Ze=（2sin*xw+2cos*yw+2n-d）*d/(sin*xw+cos*yw+n) （3）

（1）除以（2）得

Xe/Ye= (cos*xw-sin*yw+l)/ (zw+m)

(Xe*(zw+m))/Ye=cos*xw-sin*yw+l

(Xe*(zw+m))/(Ye* cos)=xw-tan*yw+l/cos

Xw=(Xe*(zw+m))/ (Ye* cos) - (ye*l)/(Ye* cos)+( sin*yw*ye)/ (Ye* cos)

Xw=(Xe*(zw+m)+ sin*yw*ye- ye*l)/ (Ye* cos)            (4)

由（2）得

Ye*(sin*xw+cos*yw+n)= (zw+m)*d

Ye*(sin*xw)+ye* cos*yw+n*ye=(zw+m)*d

把（4）代入上式得

Ye* sin*(Xe*(zw+m)+ sin*yw*ye- ye*l)/ (Ye* cos)+ye* cos*yw+n*ye=(zw+m)*d

約去ye，得

sin*(Xe*(zw+m)+ sin*yw*ye- ye*l)/ cos+ye* cos*yw+n*ye=(zw+m)*d

tan*(Xe*zw+xe*m+ sin*yw*ye- ye*l) +ye* cos*yw+n*ye=(zw+m)*d

tan*Xe*zw+xe*m *tan- ye*l*tan+ sin*tan*yw*ye+ye* cos*yw+n*ye=(zw+m)*d

(sin*tan*ye+ye* cos)*yw+ tan*Xe*zw+xe*m *tan- ye*l*tan+n*ye=(zw+m)*d

最后得

Yw=[(zw+m)*d- tan*Xe*zw- xe*m *tan+ ye*l*tan- n*ye]/ (sin*tan*ye+ye* cos) （5）

而前面已經(jīng)得到

Xw=(Xe*(zw+m)+ sin*yw*ye- ye*l)/ (Ye* cos)            (4)

實際上相當于opengl里面的逆變換，從鼠標選中的屏幕位置來確定對應(yīng)的三維空間中位置，opengl使用gluUnProject和gluUnProject4來計算。