Heavy Transportation
| Time Limit: 3000MS |
|
Memory Limit: 30000K |
| Total Submissions: 5123 |
|
Accepted: 1393 |
Description
Background
Hugo Heavy is happy. After the breakdown of the Cargolifter project he can now expand business. But he needs a clever man who tells him whether there really is a way from the place his customer has build his giant steel crane to the place where it is needed on which all streets can carry the weight.
Fortunately he already has a plan of the city with all streets and bridges and all the allowed weights.Unfortunately he has no idea how to find the the maximum weight capacity in order to tell his customer how heavy the crane may become. But you surely know.
Problem
You are given the plan of the city, described by the streets (with weight limits) between the crossings, which are numbered from 1 to n. Your task is to find the maximum weight that can be transported from crossing 1 (Hugo's place) to crossing n (the customer's place). You may assume that there is at least one path. All streets can be travelled in both directions.
Input
The first line contains the number of scenarios (city plans). For each city the number n of street crossings (1 <= n <= 1000) and number m of streets are given on the first line. The following m lines contain triples of integers specifying start and end crossing of the street and the maximum allowed weight, which is positive and not larger than 1000000. There will be at most one street between each pair of crossings.
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the maximum allowed weight that Hugo can transport to the customer. Terminate the output for the scenario with a blank line.
Sample Input
1
3 3
1 2 3
1 3 4
2 3 5
Sample Output
Scenario #1:
4
給定n個點，及m條邊的最大負載，求頂點1到頂點n的最大流。
用Dijkstra算法解之，只是需要把“最短路”的定義稍微改變一下，
A到B的路長定義為路徑上邊權最小的那條邊的長度，
而最短路其實是A到B所有路長的最大值。
//Heavy Transportation
//Dijkstra
#include <iostream>
#include<stdio.h>
using namespace std;
const int MAXS=1005;
int n;
int mat[MAXS][MAXS];
int asd[MAXS];
int s[MAXS];
int min(int a,int b)
{return a<b?a:b;}
int Dijkstra()
{
int i,j;
for(i=1;i<n;i++)
{
asd[i]=mat[0][i];
s[i]=0;
}
s[0]=1;
asd[0]=0;
for(i=0;i<n-1;i++)
{
int max=0;
int u=0;
for(j=1;j<n;j++)
{
if(s[j]==0 && asd[j]>max)
{
u=j;
max=asd[j];
}
}
if(u==0)
break;
s[u]=1;
asd[u]=max;
for(j=1;j<n;j++)
{
if (s[j]==0 && asd[j]<min(asd[u],mat[u][j]))
{
asd[j]=min(asd[u],mat[u][j]);
}
}
}
return asd[n-1];
}
int main()
{
int t,m;
int i,j;
scanf("%d",&t);
int v1,v2;
int value;
for (int s=1;s<=t;s++)
{
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)
for (j=0;j<n;j++)
{
mat[i][j]=0;
}
while (m--)
{
scanf("%d%d%d",&v1,&v2,&value);
mat[v1-1][v2-1]=mat[v2-1][v1-1]=value;
}
printf("Scenario #%d:\n%d\n\n",s,Dijkstra());
}
return 0;
}
Blocks
| Time Limit: 1000MS |
|
Memory Limit: 65536K |
| Total Submissions: 720 |
|
Accepted: 201 |
Description
Panda has received an assignment of painting a line of blocks. Since Panda is such an intelligent boy, he starts to think of a math problem of painting. Suppose there are N blocks in a line and each block can be paint red, blue, green or yellow. For some myterious reasons, Panda want both the number of red blocks and green blocks to be even numbers. Under such conditions, Panda wants to know the number of different ways to paint these blocks.
Input
The first line of the input contains an integer T(1≤T≤100), the number of test cases. Each of the next T lines contains an integer N(1≤N≤10^9) indicating the number of blocks.
Output
For each test cases, output the number of ways to paint the blocks in a single line. Since the answer may be quite large, you have to module it by 10007.
Sample Input
2
1
2
Sample Output
2
6
Source
給定一塊有n個點的木塊，用四種顏色涂色，其中兩種顏色只能用偶數次，求有多少種涂色方法。
一看就知是生成函數，可惜從沒用過。小試身手，沒想到竟然弄出來了。結果應該是對的，就是不知過程是不是可以這樣寫。
設四種顏色分別為w，x，y，z，其中y，z只能用偶數次，我的推導過程如下：
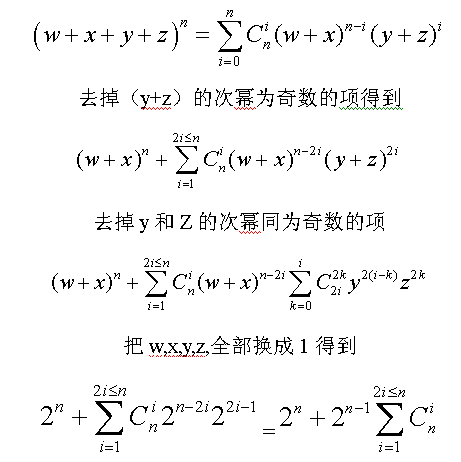
最后得到的公式是(2^( n - 1 ))(2^(n-1)+1)
注意到10007是素數,由費爾馬定理,可以先把n-1mod（10007-1）,減小計算量,剩下的就是快速取冪了.
#include <iostream>
using namespace std;
const int mod=10007;
int pow(int n)
{
if(n==0)
return 1;
if(n&1)
{
return (pow(n-1)<<1)%mod;
}
else
{
int temp=pow(n>>1);
return (temp*temp)%mod;
}
}
int main(int argc, char *argv[])
{
int t,n,temp;
cin>>t;
while(t--)
{
cin>>n;
temp=pow((n-1)%(mod-1));
cout<<(temp*(temp+1))%mod<<endl;
}
return 0;
}
//由于近日POJ登不上，上面的代碼未曾提交過
Euclid's Game
|
Time Limit: 1000MS |
|
Memory Limit: 65536K |
|
Total Submissions: 4525 |
|
Accepted: 1849 |
Description
Two players, Stan and Ollie, play, starting with two natural numbers. Stan, the first player, subtracts any positive multiple of the lesser of the two numbers from the greater of the two numbers, provided that the resulting number must be nonnegative. Then Ollie, the second player, does the same with the two resulting numbers, then Stan, etc., alternately, until one player is able to subtract a multiple of the lesser number from the greater to reach 0, and thereby wins. For example, the players may start with (25,7):
25 7
11 7
4 7
4 3
1 3
1 0
an Stan wins.
Input
The input consists of a number of lines. Each line contains two positive integers giving the starting two numbers of the game. Stan always starts.
Output
For each line of input, output one line saying either Stan wins or Ollie wins assuming that both of them play perfectly. The last line of input contains two zeroes and should not be processed.
Sample Input
34 12
15 24
0 0
Sample Output
Stan wins
Ollie wins
Source
Waterloo local 2002.09.28
給定兩堆石子,二人輪流取子,要求只能從石子數目較大的那一堆取子,取子的數目只能是另一堆石子數目的倍數.最終使得某一堆數目為零的一方為勝.
首先,容易看出,對于每一個局面,要么是先手必勝,要么是后手必勝,最終結果完全由當前局面完全確定.
另外,可以簡單羅列一下先手必勝和必敗的幾種局面(兩堆石子初始數目都大于零):
1,有一堆石子數目為一,先手必勝,? 1,4,??? 1,2.
2,兩堆石子數目差一,且兩堆石子數目都不為一,先手必敗(只能使后手面對必勝的局面),如? 3,4? 5,6?? .
3,如果數目較大的那一堆是數目較小那一堆的2倍加減一,且不是上面兩種局面,先手必勝,2,5? 3,5? 3,7.
可是上面這些信息對于解決這個問題還是有一些困難.
再進一步試算數目較小的石子,可以發現,當兩堆數目相差較大時,總是先手必勝.
事實上,進一步探討可以發現下面的結論:
1,N<2*M-1時,先手別無選擇,只能使之變為 N-M,M 局面,(易見)如3,5? 5,7? 7,4...
2,設兩堆石子數目為N,M(N>M>0,且N,M互質),則若N>=2*M-1,且N - M ! =1時,先手必勝.要求M,N互質是因為對于M,N有公因數的情形,可以同時除以其公因數而不影響結果.
簡單說明一下上面結論2的由來. N>=2*M-1時,先手可使之變為? N%M,M? 或N%M+M,M兩種局面之一,其中有且只有一個必敗局面。注意到如果N%M,M不是必敗局面，那么N%M+M,M就是必敗局面，因為面對N%M+M,M這個局面，你別無選擇，只能在前一堆中取M個使對方面對必勝局面(結論1 )。
據此可設計算法如下:
1.M,N先同時除以它們的最大公因數.(M<N)
2,如果M==0,則返回零;
3,如果M==1,則返回一;
4,如果N>=M*2-1,則返回一
5,令N=M,M=N-M,遞歸處理
#include?<iostream>
using?namespace?std;
long?long?gcd(long?long?a,long?long?b)
{
????if(a==0)
????????return?b;
????return?gcd(b%a,a);
}
long?long?Eu(long?long?m,long?long?n)
{
????if(m==1)
????????return?1;
????if(n-m==1?&&?m)
????????return?0;
????if(n>=m*2-1)
????????return?1;
????return?!Eu(n%m,m);
}
int??main()
{
????long?long?m,n,temp;
????while?(cin>>m>>n?&&?(m||n))
????{
????????long?long?g=gcd(m,n);
????????m/=g;
????????n/=g;
????????if(m>n)
????????{
????????????temp=m;
????????????m=n;
????????????n=temp;
????????}
????????if(Eu(m,n))
????????????cout<<"Stan?wins"<<endl;
????????else
????????????cout<<"Ollie?wins"<<endl;
????}
????
????return?0;
}
Rank List
|
Time Limit: 10000MS |
|
Memory Limit: 65536K |
|
Total Submissions: 6561 |
|
Accepted: 2091 |
Description
Li Ming is a good student. He always asks the teacher about his rank in his class after every exam, which makes the teacher very tired. So the teacher gives him the scores of all the student in his class and asked him to get his rank by himself. However, he has so many classmates, and he can’t know his rank easily. So he tends to you for help, can you help him?
Input
The first line of the input contains an integer N (1 <= N <= 10000), which represents the number of student in Li Ming’s class. Then come N lines. Each line contains a name, which has no more than 30 letters. These names represent all the students in Li Ming’s class and you can assume that the names are different from each other.
In (N+2)-th line, you'll get an integer M (1 <= M <= 50), which represents the number of exams. The following M parts each represent an exam. Each exam has N lines. In each line, there is a positive integer S, which is no more then 100, and a name P, which must occur in the name list described above. It means that in this exam student P gains S scores. It’s confirmed that all the names in the name list will appear in an exam.
Output
The output contains M lines. In the i-th line, you should give the rank of Li Ming after the i-th exam. The rank is decided by the total scores. If Li Ming has the same score with others, he will always in front of others in the rank list.
Sample Input
3
Li Ming
A
B
2
49 Li Ming
49 A
48 B
80 A
85 B
83 Li Ming
Sample Output
1
2
Source
POJ Monthly,Li Haoyuan
給定每個人的成績，查詢某一人的名次。
用MAP建立人名和成績的對應關系，用cnt數組（最多5000個元素）記錄成績為某個分數的人數，不過由于總人數較少(最多只有10000人),直接遍歷也不比建立計數排序數組多用多少時間,計數排序的優勢并不顯著.
用hash函數或者二分查找也應該能解決這個問題.
/**//*Source?Code
Problem:?2153??User:?y09
Memory:?1236K??Time:?1204MS?
Language:?C++??Result:?Accepted?
Source?Code?*/
#include?<iostream>
#include<string>
#include<map>
using?namespace?std;
int?main(int?argc,?char?*argv[])
{
????int?n,m;
????int?i,j;
????char?str[200];
????string?str1;
????
????map<string?,int>score;
????
????scanf("%d",&n);
????getchar();
????for?(i=0;i<n;i++?)
????{
????????gets(str);
????????str1=str;
????????score[str1]=0;
????}
????
????int?cnt[5005]={0};
????
????scanf("%d",&m);
????string?li="Li?Ming";
????int?rank=0;
????int?s=0;
????int?temp=0;
????int?temp2=0;
????int?num;
????for(int?k=0;k<m;k++)
????{
????????for(i=0;i<n;i++)
????????{
????????????scanf("%d",&num);
????????????getchar();
????????????gets(str);
????????????str1=str;
????????????temp2=score[str1];
????????????score[str1]=num+temp2;
????????????cnt[num+temp2]++;
????????}
????????s=score[li];
????????rank=1;
????????temp+=100;
????????for(i=temp;i>s;i--)
????????{
????????????rank+=cnt[i];
????????????cnt[i]=0;
????????}
????????for(i=s;i>=0;i--)
????????????cnt[i]=0;
????????printf("%d\n",rank);
????}
????return?0;
}
Binary Stirling Numbers
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 1040 |
|
Accepted: 346 |
Description
The Stirling number of the second kind S(n, m) stands for the number of ways to partition a set of n things into m nonempty subsets. For example, there are seven ways to split a four-element set into two parts:
{1, 2, 3} U {4}, {1, 2, 4} U {3}, {1, 3, 4} U {2}, {2, 3, 4} U {1}
{1, 2} U {3, 4}, {1, 3} U {2, 4}, {1, 4} U {2, 3}.
There is a recurrence which allows to compute S(n, m) for all m and n.
S(0, 0) = 1; S(n, 0) = 0 for n > 0; S(0, m) = 0 for m > 0;
S(n, m) = m S(n - 1, m) + S(n - 1, m - 1), for n, m > 0.
Your task is much "easier". Given integers n and m satisfying 1 <= m <= n, compute the parity of S(n, m), i.e. S(n, m) mod 2.
Example
S(4, 2) mod 2 = 1.
Task
Write a program which for each data set:
reads two positive integers n and m,
computes S(n, m) mod 2,
writes the result.
Input
The first line of the input contains exactly one positive integer d equal to the number of data sets, 1 <= d <= 200. The data sets follow.
Line i + 1 contains the i-th data set - exactly two integers ni and mi separated by a single space, 1 <= mi <= ni <= 10^9.
Output
The output should consist of exactly d lines, one line for each data set. Line i, 1 <= i <= d, should contain 0 or 1, the value of S(ni, mi) mod 2.
Sample Input
1
4 2
Sample Output
1
Source
判斷第二類斯特靈數模 2 的余數。
在劉汝佳的黑書上有詳細解答，基本思路是枚舉數值較小的斯特靈數，從中尋找規律。
下面這幅圖是從維基百科截出來的，有一個二進制斯特靈數與組合數的轉化公式。而組合數模二的余數就很容易了。
我們知道，組合數C（N,M）=N ! / M ! /(N-M)!,因而只需求得階乘質因數分解式中二的重數即可解決問題。
而N ！質因數分解后2的重數可用下式來計算之。
K=N/2+N/2^2+N/2^3+....
上式的除法全是下取整。（可參見任何一本初等數論課本，如北大潘承洞編的那本《初等數論》）。
這樣，這個問題就迎刃而解。
另外，有一點說明的是上面那個圖形，就是分形幾何中一個很重要的例子——謝彬斯基墊片。楊輝三角也有類似的形狀。
這是我用MATLAB作的一個楊輝三角的二進制圖形。
#include <stdio.h>
int main(int argc, char *argv[])
{
int n,m;
int z,w1,w2;
int t;
int a,b,c;
scanf("%d",&t);
while (t--)
{
scanf("%d%d",&n,&m);
z=n-(m+2)/2;
w1=(m-1)/2;
w2=z-w1;
a=0;
while (z)
{
z>>=1;
a+=z;
}
b=0;
while (w1)
{
w1>>=1;
b+=w1;
}
c=0;
while (w2)
{
w2>>=1;
c+=w2;
}
printf("%d\n",(a-b-c)==0);
}
return 0;
}
Matrix Multiplication
| Time Limit: 2000MS |
|
Memory Limit: 65536K |
| Total Submissions: 11924 |
|
Accepted: 2408 |
Description
You are given three n × n matrices A, B and C. Does the equation A × B = C hold true?
Input
The first line of input contains a positive integer n (n ≤ 500) followed by the the three matrices A, B and C respectively. Each matrix's description is a block of n × n integers.
It guarantees that the elements of A and B are less than 100 in absolute value and elements of C are less than 10,000,000 in absolute value.
Output
Output "YES" if the equation holds true, otherwise "NO".
Sample Input
2
1 0
2 3
5 1
0 8
5 1
10 26
Sample Output
YES
Hint
Multiple inputs will be tested. So O(n3) algorithm will get TLE.
Source
給定矩陣A和B，判斷矩陣C是不是它們的乘積。
題目明確表示直接判斷會超時，而Strass和直接相乘的O（n^3）效果相差不多。
因而采用隨機化方法，按我自己的想法，隨機測試C中的若干元素，以確定結果，看了討論區，才發現有更加“專業”的辦法。
隨機生成行向量I，則若A*B=C，那么必有I*A*B=I*C；反之，不一定成立，算法的隨機性正體現在這里。
用一個必要不充分條件來判斷結果的正確性，比盲目測試效果往往要好得多。
這個必要條件判斷結果的時間復雜度是O（N^2）的，這是題目輸入數據量可以接受的。
/**//*Source Code
Problem: 3318 User: y09
Memory: 3080K Time: 1063MS
Language: C Result: Accepted
Source Code */
#include <stdio.h>
#include <time.h>
#include<stdlib.h>
int main()
{
int n;
int i,j;
int mat1[500][500];
int mat2[500][500];
int mat3[500][500];
__int64 te1[500]={0};
__int64 te2[500]={0};
__int64 te3[500]={0};
__int64 te4[500]={0};
time_t t;
srand((unsigned) time(&t));
scanf("%d",&n);
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&mat1[i][j]);
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&mat2[i][j]);
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&mat3[i][j]);
for(i=0;i<n;i++)
te1[i]=rand()%100;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
te2[i]+=te1[j]*mat1[j][i];
for(i=0;i<n;i++)
for(j=0;j<n;j++)
te3[i]+=te2[j]*mat2[j][i];
for(i=0;i<n;i++)
for(j=0;j<n;j++)
te4[i]+=te1[j]*mat3[j][i];
for(i=0;i<n;i++)
if(te3[i]!=te4[i])
{
puts("NO");
return 0;
}
puts("YES");
return 0;
}
Mobile phones
| Time Limit: 5000MS |
|
Memory Limit: 65536K |
| Total Submissions: 7087 |
|
Accepted: 3030 |
Description
Suppose that the fourth generation mobile phone base stations in the Tampere area operate as follows. The area is divided into squares. The squares form an S * S matrix with the rows and columns numbered from 0 to S-1. Each square contains a base station. The number of active mobile phones inside a square can change because a phone is moved from a square to another or a phone is switched on or off. At times, each base station reports the change in the number of active phones to the main base station along with the row and the column of the matrix.
Write a program, which receives these reports and answers queries about the current total number of active mobile phones in any rectangle-shaped area.
Input
The input is read from standard input as integers and the answers to the queries are written to standard output as integers. The input is encoded as follows. Each input comes on a separate line, and consists of one instruction integer and a number of parameter integers according to the following table.
The values will always be in range, so there is no need to check them. In particular, if A is negative, it can be assumed that it will not reduce the square value below zero. The indexing starts at 0, e.g. for a table of size 4 * 4, we have 0 <= X <= 3 and 0 <= Y <= 3.
Table size: 1 * 1 <= S * S <= 1024 * 1024
Cell value V at any time: 0 <= V <= 32767
Update amount: -32768 <= A <= 32767
No of instructions in input: 3 <= U <= 60002
Maximum number of phones in the whole table: M= 2^30
Output
Your program should not answer anything to lines with an instruction other than 2. If the instruction is 2, then your program is expected to answer the query by writing the answer as a single line containing a single integer to standard output.
Sample Input
0 4
1 1 2 3
2 0 0 2 2
1 1 1 2
1 1 2 -1
2 1 1 2 3
3
Sample Output
3
4
Source
一維樹狀數組用一維數組來存儲部分元素的和，二維樹狀數組只需用二維數組來存儲即可，獲得和，修正的函數同一維數組差別不大。
/**//*Source Code
Problem: 1195 User: y09
Memory: 4956K Time: 579MS
Language: C++ Result: Accepted
Source Code */
#include <stdio.h>
const int MAX=1200;
int c[MAX][MAX];
int n;
int LowBit(int t)
{
return t&(t^(t-1));
}
int Sum(int endx,int endy)
{
int sum=0;
int temp=endy;
while(endx>0)
{
endy=temp;//注意記錄endy的值，本人在此出錯，找半天錯誤不得
while (endy>0)
{
sum+=c[endx][endy];
endy-=LowBit(endy);
}
endx-=LowBit(endx);
}
return sum;
}
void plus(int posx,int posy,int num)
{
int temp=posy;
while (posx <=n)
{
posy=temp;
while(posy<=n)
{
c[posx][posy]+=num;
posy+=LowBit(posy);
}
posx+=LowBit(posx);
}
}
int GetSum(int l,int b,int r,int t)
{
return Sum(r,t)-Sum(r,b-1)-Sum(l-1,t)+Sum(l-1,b-1);
}
int main()
{
int I;
int x,y,a;
int l,b,r,t;
while(scanf("%d",&I))
{
switch (I)
{
case 0:
scanf("%d",&n);
break;
case 1:
scanf("%d%d%d",&x,&y,&a);
plus(x+1,y+1,a);
break;
case 2:
scanf("%d%d%d%d",&l,&b,&r,&t);
printf("%d\n",GetSum(l+1,b+1,r+1,t+1));
break;
case 3:
return 0;
}
}
return 0;
}
Cipher
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 12776 Accepted: 3194
Description
Bob and Alice started to use a brand-new encoding scheme. Surprisingly it is not a Public Key Cryptosystem, but their encoding and decoding is based on secret keys. They chose the secret key at their last meeting in Philadelphia on February 16th, 1996. They chose as a secret key a sequence of n distinct integers, a1 ; . . .; an, greater than zero and less or equal to n. The encoding is based on the following principle. The message is written down below the key, so that characters in the message and numbers in the key are correspondingly aligned. Character in the message at the position i is written in the encoded message at the position ai, where ai is the corresponding number in the key. And then the encoded message is encoded in the same way. This process is repeated k times. After kth encoding they exchange their message.
The length of the message is always less or equal than n. If the message is shorter than n, then spaces are added to the end of the message to get the message with the length n.
Help Alice and Bob and write program which reads the key and then a sequence of pairs consisting of k and message to be encoded k times and produces a list of encoded messages.
Input
The input file consists of several blocks. Each block has a number 0 < n <= 200 in the first line. The next line contains a sequence of n numbers pairwise distinct and each greater than zero and less or equal than n. Next lines contain integer number k and one message of ascii characters separated by one space. The lines are ended with eol, this eol does not belong to the message. The block ends with the separate line with the number 0. After the last block there is in separate line the number 0.
Output
Output is divided into blocks corresponding to the input blocks. Each block contains the encoded input messages in the same order as in input file. Each encoded message in the output file has the lenght n. After each block there is one empty line.
Sample Input
10
4 5 3 7 2 8 1 6 10 9
1 Hello Bob
1995 CERC
0
0
Sample Output
BolHeol b
C RCE
Source
Central Europe 1995
給定1~n的置換F,求其變換m次的變換F^m.
先找到循環節,再用m對循環節的長度取模即可.
#include <iostream>
using namespace std;
int main()
{
const int MAX=300;//最大長度
char str[MAX];//讀入串
int n;//變換的長度
int data[MAX]={0};//存放原始變換
int used[MAX]={0};//標志數組
int cir[MAX][MAX]={0};//每個循環節的成員
int num[MAX]={0};//循環節對應長度
int cnt=0;//循環節的個數
int time=0;//變換次數
int change[MAX]={0};//原始循環變換time次之后的變換
char res[MAX]={0};//變換之后的字符串
int i,j;
while(cin>>n && n)
{
memset(used,0,sizeof(used));
memset(num,0,sizeof(num));
for(i=1;i<=n;i++)
cin>>data[i];
cnt=0;//計數循環節個數
for(i=1;i<=n;i++)
{
if(used[i]==0)
{
used[i]=1;
int temp=data[i];
cir[cnt][num[cnt]]=temp;
num[cnt]=1;
while(used[temp]==0)//獲得循環節
{
used[temp]=1;
temp=data[temp];
cir[cnt][num[cnt]++]=temp;
}
cnt++;
}
}
while(cin>>time && time)//讀入變換次數
{
memset(res,0,sizeof(res));
memset(str,0,sizeof(str));
gets(str);
int len=strlen(str);
for(i=len;i<=n;i++)//位數不足n,補空格
str[i]=' ';
//獲得變換
for(i=0;i<cnt;i++)
{
for(j=0;j<num[i];j++)
{
change[cir[i][j]]=cir[i][(j+time)%num[i]];
}
}
//對讀入數據變換,獲得結果
for(i=1;i<=n;i++)
{
res[change[i]]=str[i];
}
cout<<res+1<<endl;
}
cout<<endl;
}
return 0;
}
題意簡單,就是找四個數的和為零.先把前兩列的和算出來,O(n^2),存到hash表中,再把后兩列的兩兩和算出來,在hash表中找相反數.用線性探測法就可以解決該問題了.
/**//*Source CodeProblem: 2785 User: y09shendazhi
Memory: 160132K Time: 2610MS
Language: G++ Result: Accepted
Source Code*/
#include <iostream>
#include<stdio.h>
using namespace std;
const int size=20345677;
int hash[size];
int sum[size];
const int key=1777;
const int MAX=1000000000;
void Insert(int num)
{
int temp=num;
num=(num+MAX)%size;
while(hash[num]!=MAX && hash[num]!=temp)
num=(key+num)%size;
hash[num]=temp;
sum[num]++;
}
int Find(int num)
{
int temp=num;
num=(num+MAX)%size;
while(hash[num]!=MAX && hash[num]!=temp)
num=(num+key)%size;
if(hash[num]==MAX)
return 0;
else
return sum[num];
}
int main()
{
int n;
int i,j;
int a[4005],b[4005],c[4005],d[4005];
scanf("%d",&n);
int ans=0;
for(i=0;i<n;i++)
{
scanf("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
}
for(i=0;i<size;i++)
{
hash[i]=MAX;
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
Insert(a[i]+b[j]);
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
ans+=Find(-(c[i]+d[j]));
}
printf("%d\n",ans);
return 0;
}
讀半天不解其意,傻算了半天才把sample湊出來.其實很簡單,連高精度都沒有.第一類斯特靈數S(n,m)就是把n元集合分成m部的個數,有遞推關系S(n,m)=S(n-1,m-1)+mS(n-1,m).所求還要全排列一下.再乘以m!就可以了累加1~B個數全部用上,就是結果.F(B)=sum(C(B,i)*(Sum(Stir( i,j )* j ! ) ) )就是結果.其中下標i從1變到B,j從1變到i.
/**//*Source CodeProblem: 3088 User: y09shendazhi
Memory: 164K Time: 0MS
Language: C++ Result: Accepte/
Source Code*/
#include <iostream>
using namespace std;
// /n\
// | |
// \m/
__int64 comb(__int64 m,__int64 n)
{
if(n<m)
return 0;
__int64 result=1;
m=m<n-m?m:n-m;
for(__int64 i=1;i<=m;i++)
result=(result*(n-m+i))/i;
return result;
}
__int64 fun(__int64 n)
{
__int64 ans=1;
for(__int64 i=1;i<=n;i++)
ans*=i;
return ans;
}
int main(__int64 argc, char *argv[])
{
__int64 i,j,k;
__int64 stir[15][15]={0};
for(i=1;i<12;i++)
{
stir[i][1]=1;
for(j=2;j<i;j++)
{
stir[i][j]=stir[i-1][j-1]+j*stir[i-1][j];
}
stir[i][i]=1;
}
__int64 ans[12]={0,1};
for(i=2;i<12;i++)
{
for(j=1;j<=i;j++)
{
__int64 temp=0;
for(k=1;k<=j;k++)
{
temp+=stir[j][k]*fun(k);
}
ans[i]+=temp*comb(j,i);
}
}
__int64 in=0;
__int64 t=0;
scanf("%d",&t);
for(i=0;i<t;i++)
{
scanf("%d",&in);
printf("%I64d %I64d %I64d\n",i+1,in,ans[in]);
}
return 0;
}