基本函數F(n)=G(n) + H(n);
其中G(n)是從起始點到當前點的距離,H(n)是從當前點到目標點的估計距離。
例如對于一個網格狀的路網可以橫走和豎走,H(n)就是標準Manhattan距離:
h(n) = D * (abs(n.x-goal.x) + abs(n.y-goal.y))
D是走一步的代價。
對于不同的情況H(n)的選取很關鍵,H越大運算時間越短但得到最優解的可能性越低
H越小運算時間越長得到最優解的可能性越高。當H為0時就是dijkstra算法。
1) 創建OPEN和CLOSE表。其中OPEN為待評估的點,CLOSE為已經運算評估過的點。其中OPEN使用二叉堆便于排序。
2) 初始化將起始點計算F(n)并加入到OPEN表。
3) 取當前OPEN中的最小F(n)點為當前點,將他從OPEN表中刪除,加入到CLOSE表。
4) 計算當前點的所有附近點(即一步能達到的點)
4.1 對于附近點計算cost=當前點的G(n)+當前點到附近點的開銷。
4.2 如果附近點已經在OPEN中則比較附近點的G(n)和cost,如果cost小于附近點的G(n)則更新OPEN表中的附近點的G(n)為cost和F(n),并把它的父節點設為當前點。反之不做操作。
4.3 如果附近點在CLOSE表中則比較附近點的G(n)和cost,如果cost小于附近點的G(n),則將附近點從CLOSE表中刪除并更新該附近點的G(n)和F(n)并加入到OPEN表,并把它的父節點設為當前點。反之不操作。
4.4 如果附近點既不在OPEN表也不在CLOSE表,則計算附近點的G(n),H(n)和F(n)并加入到OPEN表,并把它的父節點設為當前點。
5) 從3步驟開始重新計算直到當前點為目標點。
6) 從目標點開始按父節點給出到起始點的最短路徑。
其中的關鍵是對OPEN表、CLOSE表的數據結構設計。由于OPEN表中存在排序和查找的基本操作,CLOSE表也存在查找的基本操作。
當數據量大時,數據結構的優勢體現的非常明顯。OPEN表一般都使用二叉堆的形式,CLOSE表則使用簡單的數組即可。
實際測試產生一個1366*768 像素通路點和障礙點為1:2的隨機網格地圖從坐標(100, 100)到(1000, 300)的算路時間(h取Manhattan距離)在5400雙核cpu,2g內存下大概為120秒左右。

遺傳算法
網上建模實現的方法很多
第一種 針對網格狀地圖的遺傳算法
1. 將地圖抽象成網格,對于不同地形賦不同值,例如高速路標的值可以比輔路低3到4倍。
2. 旋轉地圖使起點和終點調節成位于同一個縱坐標。
3. 將起點到終點將的像素點劃分成幾個塊。
4. 對于每個塊產生隨機的基因(即變異的過程),保證每個塊的當前基因位置與前一個基因位置相差小于2個像素點(即2個基因連通)。如圖紅藍為2個獨立的染色體:
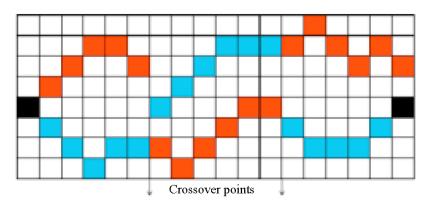
5. 計算所有染色體的適應度 。選擇最小的2個染色體作為雙親。
。選擇最小的2個染色體作為雙親。
6. 對雙親進行隨機交配產生子代。當產生的子代形成一條通路時停止。否則返回到第五步。
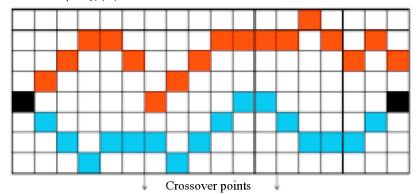
他人的運行結果:
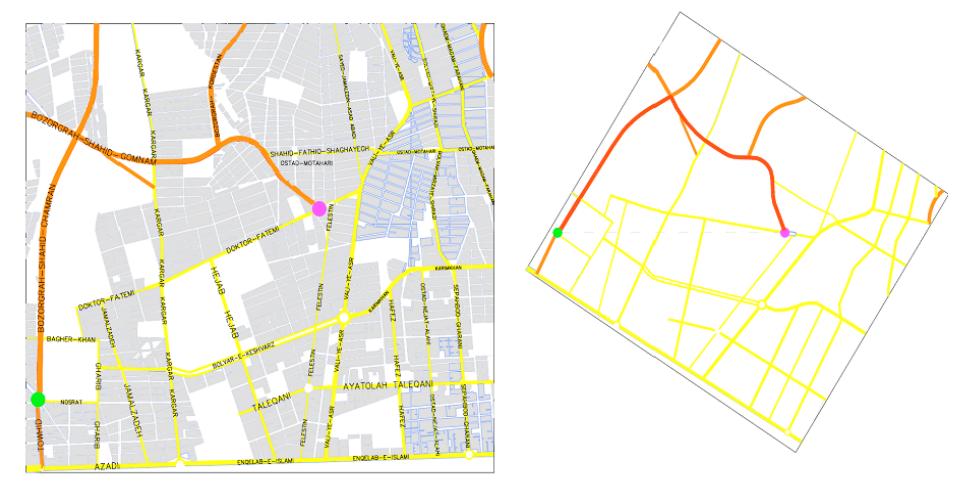
以上算法存在的最大缺陷是當存在的路徑垂直于起點和終點的連接線時,無法產生適合的基因,因為該算法產生的基因對于每一個縱坐標是唯一的。
l第二種 針對路網結構的遺傳算法
大致思想如下:
1. 針對起點和終點先產生n條連通路徑作為原始的種群。
2. 計算每條路徑的適應度(一般都以路徑的長度為基礎作為適應度)。
3. 進行隨機交配(前提是雙親必須有交叉點)。這個變化最大隨機的好壞決定了整個算法的優劣。
4. 淘汰掉適應度最低的m條道路。
5. 重復2-4步驟。設定結束條件為連續k次遺傳的最優解都是同一個或者設定遺傳的次數(到例如50次自動結束)。
6. 將適應度最高的作為最終解。
以上算法的難點在于原始種群的產生有一定難度,取小了無法滿足交叉條件,取大了耗費運算時間且復雜度提高