原文鏈接:Part3: Binary Trees and BSTs
本文是"考察數(shù)據(jù)結(jié)構(gòu)"系列文章的第三部分���,討論的是.Net Framework基類庫沒有包括的常用數(shù)據(jù)結(jié)構(gòu):
二叉樹。就像線形排列數(shù)據(jù)的數(shù)組一樣�����,我們可以將二叉樹想象為以二維方式來存儲數(shù)據(jù)��。其中一種特殊的二叉樹���,我們稱為二叉搜索樹(binary search tree)�����,簡稱為BST�����,它的數(shù)據(jù)搜索能力比一般數(shù)組更加優(yōu)化���。
目錄:
簡介
在樹中排列數(shù)據(jù)
理解二叉樹
用BSTs改善數(shù)據(jù)搜索時(shí)間
現(xiàn)實(shí)世界的二叉搜索樹
簡介:
在本系列的第一部分���,我們講述了什么是數(shù)據(jù)結(jié)構(gòu)���,怎么評估它們的性能��,以及怎樣根據(jù)其性能選擇具體的數(shù)據(jù)結(jié)構(gòu)來處理特定的算法��。另外,我們復(fù)習(xí)了數(shù)據(jù)結(jié)構(gòu)的基礎(chǔ)知識���,了解了最常用的數(shù)據(jù)結(jié)構(gòu)——數(shù)組及與其相關(guān)的ArrayList。在第二部分�����,我們講述了ArrayList的兩個(gè)兄弟——堆棧和隊(duì)列���。它們存儲數(shù)據(jù)的方式與ArrayList非常相似���,但它們訪問數(shù)據(jù)的方式受到了限制��。我們還討論了哈希表�����,它可以以任意對象作為其索引��,而非一般所用的序數(shù)�����。
ArrayList,堆棧,隊(duì)列和哈希表從存儲數(shù)據(jù)的表現(xiàn)形式看���,都可以認(rèn)為是一種數(shù)組結(jié)構(gòu)。這意味著,這四種數(shù)據(jù)結(jié)構(gòu)都將受到數(shù)組邊界的限制���。回想第一部分所講的,數(shù)組在內(nèi)存中以線形存儲數(shù)據(jù),當(dāng)數(shù)組容量到達(dá)最大值時(shí)��,需要顯式地改變其容量,同時(shí)會造成線形搜索時(shí)間的增加���。
本部分�����,我們講考察一種全新的數(shù)據(jù)結(jié)構(gòu)——二叉樹。它以一種非線性的方式存儲數(shù)據(jù)���。之后,我們還將介紹一種更具特色的二叉樹——二叉搜索樹(BST)���。BST規(guī)定了排列樹的每個(gè)元素項(xiàng)的一些規(guī)則。這些規(guī)則保證了BSTs能夠以一種低于線形搜索時(shí)間的性能來搜索數(shù)據(jù)�����。
在樹中排列數(shù)據(jù)
如果我們看過家譜,或者是一家公司的組織結(jié)構(gòu)圖�����,那么事實(shí)上你已經(jīng)明白在樹中數(shù)據(jù)的排列方式了。樹由許多節(jié)點(diǎn)的集合組成,這些節(jié)點(diǎn)又有許多相關(guān)聯(lián)的數(shù)據(jù)和“孩子”��。子節(jié)點(diǎn)就是直接處于節(jié)點(diǎn)之下的節(jié)點(diǎn)���。父節(jié)點(diǎn)則位于與節(jié)點(diǎn)直接關(guān)聯(lián)的上方���。樹的根是一個(gè)不包含父節(jié)點(diǎn)的單節(jié)點(diǎn)��。
圖1顯示了公司職員的組織結(jié)構(gòu)圖。
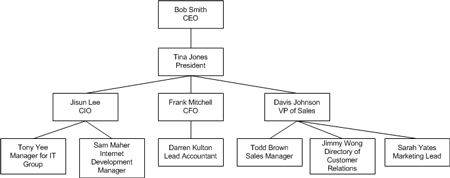
圖一
例中��,樹的根為Bob Smith,是公司的CEO�����。這個(gè)節(jié)點(diǎn)為根節(jié)點(diǎn)是因?yàn)槠渖蠜]有父親���。Bob Smith節(jié)點(diǎn)有一個(gè)孩子Tina Jones�����,公司總裁。其父節(jié)點(diǎn)為Bob Smith�����。Tina Jones有三個(gè)孩子:
Jisun Lee, CIO
Frank Mitchell, CFO
Davis Johnson, VP of Sales
這三個(gè)節(jié)點(diǎn)的父親都是Tina Jones節(jié)點(diǎn)��。
所有的樹都有如下共同的特性:
1、只有一個(gè)根�����;
2�����、除了根節(jié)點(diǎn),其他所有節(jié)點(diǎn)又且只有一個(gè)父節(jié)點(diǎn);
3���、沒有環(huán)結(jié)構(gòu)�����。從任意一個(gè)節(jié)點(diǎn)開始�����,都沒有回到起始節(jié)點(diǎn)的路徑。正是前兩個(gè)特性保證沒有環(huán)結(jié)構(gòu)的存在�����。
對于有層次關(guān)系的數(shù)據(jù)而言�����,樹非常有用。后面我們會講到,當(dāng)我們有技巧地以層次關(guān)系排列數(shù)據(jù)時(shí)�����,搜索每個(gè)元素的時(shí)間會顯著減少���。在此之前�����,我們首先需要討論的是一種特殊的樹:二叉樹���。
理解二叉樹
二叉樹是一種特殊的樹�����,因?yàn)樗乃泄?jié)點(diǎn)最多只能有兩個(gè)子節(jié)點(diǎn)���。并且��,對于二叉樹中指定的節(jié)點(diǎn)��,第一個(gè)子節(jié)點(diǎn)必須指向左孩子��,第二個(gè)節(jié)點(diǎn)指向右孩子。如圖二所示:
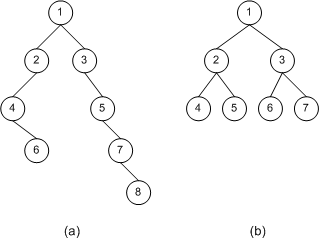
圖二
二叉樹(a)共有8個(gè)節(jié)點(diǎn),節(jié)點(diǎn)1為根��。節(jié)點(diǎn)1的左孩子為節(jié)點(diǎn)2��,右孩子為節(jié)點(diǎn)3���。注意,節(jié)點(diǎn)并不要求同時(shí)具有左孩子和右孩子���。例如��,二叉樹(a)中�����,節(jié)點(diǎn)4就只有一個(gè)右孩子。甚至于�����,節(jié)點(diǎn)也可以沒有孩子�����。如二叉樹(b),節(jié)點(diǎn)4、5���、6都沒有孩子�����。
沒有孩子的節(jié)點(diǎn)稱為葉節(jié)點(diǎn)�����。有孩子的節(jié)點(diǎn)稱為內(nèi)節(jié)點(diǎn)��。如圖二,二叉樹(a)中節(jié)點(diǎn)6��、8為葉節(jié)點(diǎn)���,節(jié)點(diǎn)1�����、2�����、3��、4���、5��、7為內(nèi)節(jié)點(diǎn)。
不幸的是�����,.Net Framework中并不包含二叉樹類�����,為了更好地理解二叉樹��,我們需要自己來創(chuàng)建這個(gè)類��。
第一步:創(chuàng)建節(jié)點(diǎn)類Node
節(jié)點(diǎn)類Node抽象地表示了樹中的一個(gè)節(jié)點(diǎn)�����。認(rèn)識到二叉樹中節(jié)點(diǎn)應(yīng)包括兩個(gè)內(nèi)容:
1�、 數(shù)據(jù)��;
2��、 子節(jié)點(diǎn):0個(gè)�、1個(gè)、2個(gè);
節(jié)點(diǎn)存儲的數(shù)據(jù)依賴于你的實(shí)際需要�。就像數(shù)組可以存儲整型、字符串和其他類類型的實(shí)例一樣,節(jié)點(diǎn)也應(yīng)該如此��。因此我們應(yīng)該將節(jié)點(diǎn)類存儲的數(shù)據(jù)類型設(shè)為object。
注意:在C# 2.0版中可以用泛型來創(chuàng)建強(qiáng)類型的節(jié)點(diǎn)類��,這樣比使用object類型更好��。要了解更多使用泛型的信息,請閱讀Juval Lowy的文章:An Introduction to C# Generics��。
下面是節(jié)點(diǎn)類的代碼:
public class Node
{
private object data;
private Node left, right;
#region Constructors
public Node() : this(null) {}
public Node(object data) : this(data, null, null) {}
public Node(object data, Node left, Node right)
{
this.data = data;
this.left = left;
this.right = right;
}
#endregion
#region Public Properties
public object Value
{
get
{
return data;
}
set
{
data = value;
}
}
public Node Left
{
get
{
return left;
}
set
{
left = value;
}
}
public Node Right
{
get
{
return right;
}
set
{
right = value;
}
}
#endregion
}
注意類Node有三個(gè)私有成員:
1、 data����,類型為object:為節(jié)點(diǎn)存儲的數(shù)據(jù);
2����、 left��,Node類型:指向Node的左孩子����;
3�、 right,Node類型:指向Node的右孩子;
4����、 類的其他部份為構(gòu)造函數(shù)和公共字段��,訪問了這三個(gè)私有成員變量����。注意����,left和right私有變量為Node類型����,就是說Node類的成員中包含Node類的實(shí)例本身。
創(chuàng)建二叉樹類BinaryTree
創(chuàng)建好Node類后��,緊接著創(chuàng)建BinaryTree類����。BinaryTree類包含了一個(gè)私有字段——root——它是Node類型,表示二叉樹的根�。這個(gè)私有字段以公有字段的方式暴露出來。
BinaryTree類只有一個(gè)公共方法Clear()��,它用來清除樹中所有元素。Clear()方法只是簡單地將根節(jié)點(diǎn)置為空null��。代碼如下:
public class BinaryTree
{
private Node root;
public BinaryTree()
{
root = null;
}
#region Public Methods
public virtual void Clear()
{
root = null;
}
#endregion
#region Public Properties
public Node Root
{
get
{
return root;
}
set
{
root = value;
}
}
#endregion
}
下面的代碼演示了怎樣使用BinaryTree類來生成與圖二所示的二叉樹(a)相同的數(shù)據(jù)結(jié)構(gòu):
BinaryTree btree = new BinaryTree();
btree.Root = new Node(1);
btree.Root.Left = new Node(2);
btree.Root.Right = new Node(3);
btree.Root.Left.Left = new Node(4);
btree.Root.Right.Right = new Node(5);
btree.Root.Left.Left.Right = new Node(6);
btree.Root.Right.Right.Right = new Node(7);
btree.Root.Right.Right.Right.Right = new Node(8);
注意,我們創(chuàng)建BinaryTree類的實(shí)例后,要?jiǎng)?chuàng)建根節(jié)點(diǎn)(root)。我們必須人工地為相應(yīng)的左、右孩子添加新節(jié)點(diǎn)類Node的實(shí)例��。例如,添加節(jié)點(diǎn)4��,它是根節(jié)點(diǎn)的左節(jié)點(diǎn)的左節(jié)點(diǎn),我們的代碼是:
btree.Root.Left.Left = new Node(4);
回想一下我們在第一部分中提到的數(shù)組元素,使存放在連續(xù)的內(nèi)存塊中,因此定位時(shí)間為常量。因此����,訪問特定元素所耗費(fèi)時(shí)間與數(shù)組增加的元素個(gè)數(shù)無關(guān)�。
然而����,二叉樹卻不是連續(xù)地存放在內(nèi)存中,如圖三所示��。事實(shí)上,BinaryTree類的實(shí)例指向root Node類實(shí)例��。而root Node類實(shí)例又分別指向它的左右孩子節(jié)點(diǎn)實(shí)例����,以此類推�。關(guān)鍵在于,組成二叉樹的不同的Node實(shí)例是分散地放在CLR托管堆中�。他們沒有必要像數(shù)組元素那樣連續(xù)存放�。

圖三
如果我們要訪問二叉樹中的特定節(jié)點(diǎn)����,我們需要搜索二叉樹的每個(gè)節(jié)點(diǎn)。它不能象數(shù)組那樣根據(jù)指定的節(jié)點(diǎn)直接訪問����。搜索二叉樹要耗費(fèi)線性時(shí)間��,最壞情況是查詢所有的節(jié)點(diǎn)。也就是說�,當(dāng)二叉樹節(jié)點(diǎn)個(gè)數(shù)增加時(shí)�,查找任意節(jié)點(diǎn)的步驟數(shù)也將相應(yīng)地增加��。
因此�,如果二叉樹的定位時(shí)間為線性����,查詢時(shí)間也為線性,那怎么說二叉樹比數(shù)組更好呢����?因?yàn)閿?shù)組的查詢時(shí)間雖然也是線性�,但定位時(shí)間卻是常量?���。渴堑?,一般的二叉樹確實(shí)不能提供比數(shù)組更好的性能�。然而當(dāng)我們有技巧地排列二叉樹中的元素時(shí)�,我們就能很大程度改善查詢時(shí)間(當(dāng)然,定位時(shí)間也會得到改善)��。
用BSTs改善數(shù)據(jù)搜索時(shí)間
二叉搜索樹是一種特殊的二叉樹����,它改善了二叉樹數(shù)據(jù)搜索的效率��。二叉搜索樹有以下屬性:對于任意一個(gè)節(jié)點(diǎn)n����,其左子樹下的每個(gè)后代節(jié)點(diǎn)的值都小于節(jié)點(diǎn)n的值��;而其右子樹下的每個(gè)后代節(jié)點(diǎn)的值都大于節(jié)點(diǎn)n的值��。
所謂節(jié)點(diǎn)n的子樹,可以將其看作是以節(jié)點(diǎn)n為根節(jié)點(diǎn)的樹。因此,子樹的所有節(jié)點(diǎn)都是節(jié)點(diǎn)n的后代����,而子樹的根則是節(jié)點(diǎn)n本身。圖四演示了子樹的概念和二叉搜索樹的屬性。

圖四
圖五顯示了二叉樹的兩個(gè)例子。圖右��,二叉樹(b),是一個(gè)二叉搜索樹(BST),因?yàn)樗隙嫠阉鳂涞膶傩浴6鏄洌?/SPAN>a)�,則不是二叉搜索樹��。因?yàn)楣?jié)點(diǎn)10的右孩子節(jié)點(diǎn)8小于節(jié)點(diǎn)10,但卻出現(xiàn)在節(jié)點(diǎn)10的右子樹中����。同樣����,節(jié)點(diǎn)8的右孩子節(jié)點(diǎn)4小于節(jié)點(diǎn)8,卻出現(xiàn)在了它的右子樹中�。不管是在哪個(gè)位置,不符合二叉搜索樹的屬性規(guī)定��,就不是二叉搜索樹。例如��,節(jié)點(diǎn)9的右子樹只能包含值小于節(jié)點(diǎn)9的節(jié)點(diǎn)(8和4)����。
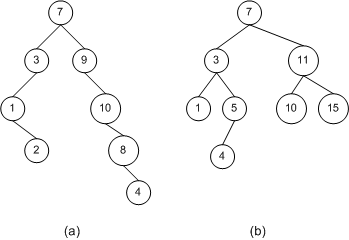
圖五
從二叉搜索樹的屬性可知��,BST各節(jié)點(diǎn)存儲的數(shù)據(jù)必須和另外的節(jié)點(diǎn)進(jìn)行比較�。給出任意兩個(gè)節(jié)點(diǎn)�,BST必須能夠判斷這兩個(gè)節(jié)點(diǎn)的值是小于�、大于還是等于����。
現(xiàn)在��,設(shè)想一下�,我們要查找BST的某個(gè)特定的節(jié)點(diǎn)����。例如圖五中的二叉搜索樹(b),我們要查找節(jié)點(diǎn)10��。BST和一般的二叉樹一樣����,都只有一個(gè)根節(jié)點(diǎn)。那么如果節(jié)點(diǎn)10存在于樹中,搜索這棵樹的最佳方案是什么��?有沒有比搜索整棵樹更好的方法�?
如果節(jié)點(diǎn)10存在于樹中����,我們從根開始?���?梢钥吹剑?jié)點(diǎn)的值為7�,小于我們要查找的節(jié)點(diǎn)值����。因此��,一旦節(jié)點(diǎn)10存在�,必然存在其右子樹��。所以應(yīng)該跳到節(jié)點(diǎn)11繼續(xù)查找��。此時(shí),節(jié)點(diǎn)10小于節(jié)點(diǎn)11的值��,必然存在于節(jié)點(diǎn)11的左子樹中����。移到節(jié)點(diǎn)11的左孩子��,此時(shí)我們已經(jīng)找到了目標(biāo)節(jié)點(diǎn),定位于此��。
如果我們要查找的節(jié)點(diǎn)在樹中不存在�,會發(fā)生問題�?例如我們查找節(jié)點(diǎn)9����。重復(fù)上述操作�,直到到達(dá)節(jié)點(diǎn)10,它大于節(jié)點(diǎn)9��,那么如果節(jié)點(diǎn)9存在,必然是在節(jié)點(diǎn)10的左子樹中��。然而我們看到節(jié)點(diǎn)10根本就沒有左孩子��,因此節(jié)點(diǎn)9在樹中不存在。
正式地����,我們的搜索算法如下所示�。假定我們要查找節(jié)點(diǎn)n,此時(shí)已指向BST的根節(jié)點(diǎn)����。算法不斷地比較數(shù)值的大小直到找到該節(jié)點(diǎn)��,或指為空值�。每一步我們都要處理兩個(gè)節(jié)點(diǎn):樹中的節(jié)點(diǎn)c,要查找的節(jié)點(diǎn)n,并比較c和n的值。C的初始化值為BST根節(jié)點(diǎn)的值�。然后執(zhí)行以下步驟:
1����、 如果c值為null����,則n不在BST中;
2�、 比較c和n的值;
3����、 如果值相同����,則找到了指定節(jié)點(diǎn)n��;
4��、 如果n的值小于c�,那么如果n存在�,必然在c的左子樹中。因此回到第一步����,將c的左孩子作為c�;
5、 如果n的值大于c��,那么如果n存在��,必然在c的右子樹中。因此回到第一步��,將c的右孩子作為c�;
分析BST搜索算法
通過BST查找節(jié)點(diǎn),理想情況下我們需要檢查的節(jié)點(diǎn)數(shù)可以減半����。如圖六的BST樹�,包含了15個(gè)節(jié)點(diǎn)�。從根節(jié)點(diǎn)開始執(zhí)行搜索算法,第一次比較決定我們是移向左子樹還是右子樹�。對于任意一種情況����,一旦執(zhí)行這一步��,我們需要訪問的節(jié)點(diǎn)數(shù)就減少了一半�,從15降到了7�。同樣,下一步訪問的節(jié)點(diǎn)也減少了一半��,從7降到了3�,以此類推。
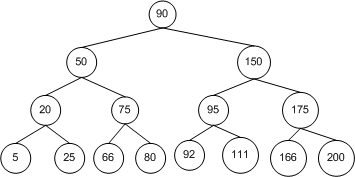
圖六
這里一個(gè)重要概念就是算法的每一步在理想狀態(tài)下都將使被訪問的節(jié)點(diǎn)數(shù)減少一半。比較一下數(shù)組的搜索算法����。搜索數(shù)組時(shí)�,要搜索所有所有元素��,每個(gè)元素搜索一次��。也就是說,搜索有n個(gè)元素的數(shù)組��,從第一個(gè)元素開始�,我們要訪問n-1個(gè)元素。而有n個(gè)節(jié)點(diǎn)的二叉搜索樹����,在訪問了根節(jié)點(diǎn)后��,只需要再搜索n/2個(gè)節(jié)點(diǎn)����。
搜索二叉樹與搜索排序數(shù)組相似。例如,你要在電話薄中查找是否有John King�。你可以從電話薄的中間開始查找��,即從以M開頭的姓氏開始查找。按照字母順序,K是在M之前,那么你可以將M之前的部分在折半����,此時(shí)�,可能是字母H��。因?yàn)?/SPAN>K是在H之后�,那么再將H到M這部分折半��。這次你找到了字母K����,你可以馬上看到電話薄里有沒有James King�。
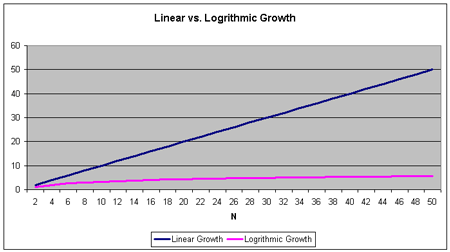
搜索BST與之相似。BST的中點(diǎn)是根節(jié)點(diǎn)�。然后從上到下��,瀏覽你所需要的左孩子或右孩子。每一步都將節(jié)約一半的搜索時(shí)間����。根據(jù)這一特點(diǎn)��,這個(gè)算法的時(shí)間復(fù)雜度應(yīng)該是log2n����,簡寫為log n����?�;叵胛覀冊诘谝徊糠钟懻摰臄?shù)學(xué)問題����,log2n = y,相當(dāng)于2y = n����。即�,節(jié)點(diǎn)數(shù)增加n��,搜索時(shí)間只緩慢地增加到log2n����。圖七表示了log2n和線性增長的增長率之間的區(qū)別��。時(shí)間復(fù)雜度為log2n的算法運(yùn)行時(shí)間為下面那條直線�。
圖七
可以看出�,這條對數(shù)曲線幾乎是水平線,隨著N值的增加�,曲線增長緩慢����。舉例來說吧��,搜索一個(gè)具有1000個(gè)元素的數(shù)組�,需要查詢1000個(gè)元素�,而搜索一個(gè)具有1000個(gè)元素的BST樹,僅需要查詢不到10個(gè)節(jié)點(diǎn)(log10 1024 = 10)��。
在分析BST搜索算法中����,我不斷地重復(fù)“理想地(ideally)”這個(gè)字眼兒。這是因?yàn)?/SPAN>BST實(shí)際的搜索時(shí)間要依賴于節(jié)點(diǎn)的拓?fù)浣Y(jié)構(gòu)�,也就是說節(jié)點(diǎn)之間的布局關(guān)系��。象圖六中所示的二叉樹����,每一步比較操作都可以使搜索時(shí)間減半。然而����,我們來看看圖八所示的BST樹,它的拓?fù)浣Y(jié)構(gòu)是與數(shù)組的排列方式是同構(gòu)的��。
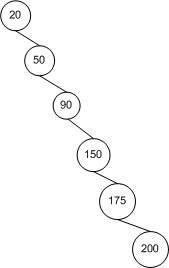
圖八
搜索圖八中的BST樹,仍然要耗費(fèi)線性時(shí)間����,因?yàn)槊勘容^一步��,都緊緊減少了一個(gè)節(jié)點(diǎn)�,而非像圖六中那樣減半�。
因此,搜索BST所耗費(fèi)的時(shí)間要依賴于它的拓?fù)浣Y(jié)構(gòu)����。最佳情況下,耗費(fèi)時(shí)間為log2 n�,最壞情況則要耗費(fèi)線性時(shí)間�。在下一節(jié)我們將看到,BST的拓?fù)浣Y(jié)構(gòu)與插入節(jié)點(diǎn)的順序有關(guān)��。因此,插入節(jié)點(diǎn)的順序?qū)⒅苯佑绊?/SPAN>BST搜索算法的耗時(shí)����。
插入節(jié)點(diǎn)到BST中
我們已經(jīng)知道了在BST中查詢一個(gè)特定節(jié)點(diǎn)的方法����,但是我們還應(yīng)該掌握插入一個(gè)新節(jié)點(diǎn)的方法�。向二叉搜索樹插入一個(gè)新節(jié)點(diǎn)��,不能任意而為�,必須遵循二叉搜索樹的特性����。
通常我們插入的新節(jié)點(diǎn)都是作為葉節(jié)點(diǎn)��。唯一的問題是,怎樣查找合適的節(jié)點(diǎn),使其成為這個(gè)新節(jié)點(diǎn)的父節(jié)點(diǎn)��。與搜索算法相似��,我們首先應(yīng)該比較節(jié)點(diǎn)c和要插入的新節(jié)點(diǎn)n�。我們還需要跟蹤節(jié)點(diǎn)c的父節(jié)點(diǎn)�。初始狀態(tài)下,c節(jié)點(diǎn)為樹的根節(jié)點(diǎn)��,父節(jié)點(diǎn)為null��。定位一個(gè)新的父節(jié)點(diǎn)遵循如下算法:
1�、 如果c指向null����,則c節(jié)點(diǎn)作為n的父節(jié)點(diǎn)。如果n的值小于父節(jié)點(diǎn)值����,則n為父節(jié)點(diǎn)新的左孩子����,否則為右孩子�;
(譯注:原文為If c is a null reference,then parent will be the parent of n.. If n’s value is less than parent’s value,then n will be parent’s new left child; otherwise n will be parent’s new right child. 那么翻譯過來就是如果c的值為空,當(dāng)前父節(jié)點(diǎn)為n的父節(jié)點(diǎn)。筆者以為這似乎有誤��。因?yàn)槿绻?/SPAN>c值為空�,則說明BST樹為空����,沒有任何節(jié)點(diǎn),此時(shí)應(yīng)為后面講到的特殊情況����。如果是說c指向null�。那么說明c為葉節(jié)點(diǎn)��,則新插入的節(jié)點(diǎn)應(yīng)作為c的孩子�。即c作為n的父節(jié)點(diǎn)����,也不是原文所說的c的父節(jié)點(diǎn)作為n的父節(jié)點(diǎn))
2、 比較n和c的值;
3、 如果c等于n�,則用于試圖插入一個(gè)相同的節(jié)點(diǎn)�。此時(shí)要么直接拋棄該節(jié)點(diǎn)��,要么拋出異常��。(注意,在BST中節(jié)點(diǎn)的值必須是唯一的。)
4、 如果n小于c,則n必然在c的左子樹中����。讓父節(jié)點(diǎn)等于c�,c等于c的左孩子��,返回到第一步����。
5�、 如果n大于c,則n必然在c的右子樹中�。讓父節(jié)點(diǎn)等于c�,c等于c的右孩子��,返回到第一步。
當(dāng)合適的葉節(jié)點(diǎn)找到后�,算法結(jié)束�。將新節(jié)點(diǎn)放到BST中使其成為父節(jié)點(diǎn)合適的孩子節(jié)點(diǎn)����。插入算法中有種特例需要考慮。如果BST樹中沒有根節(jié)點(diǎn)�,則父節(jié)點(diǎn)為空��,那么添加新節(jié)點(diǎn)作為父節(jié)點(diǎn)的孩子這一步就忽略。而且在這種情況下����,BST的根節(jié)點(diǎn)必須分配為新節(jié)點(diǎn)��。
圖九描述了BST插入算法:
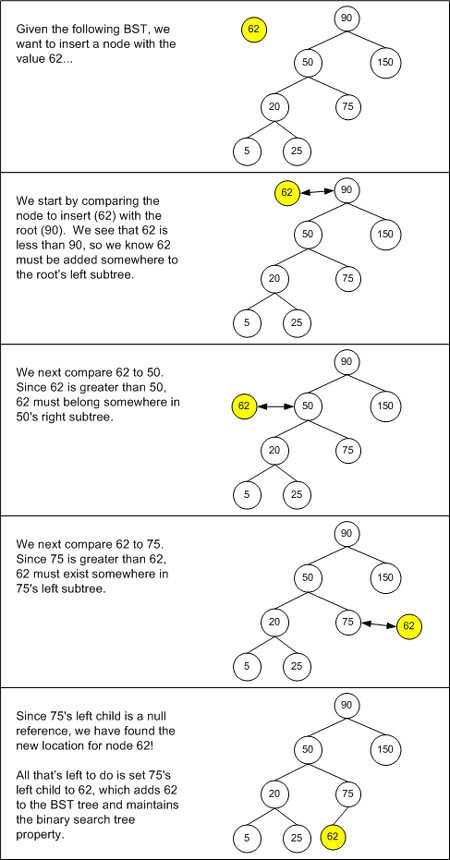
圖九
BST插入算法和搜索算法時(shí)間復(fù)雜度一樣:最佳情況為log2 n,最壞情況為線性時(shí)間�。之所以相同�,是因?yàn)樗鼮椴迦氲男鹿?jié)點(diǎn)定位所采取的策略是一致的。
節(jié)點(diǎn)插入順序決定BST的拓?fù)浣Y(jié)構(gòu)
既然新插入的節(jié)點(diǎn)是作為葉節(jié)點(diǎn)插入的�,則插入的順序?qū)⒅苯佑绊?/SPAN>BST自身的拓?fù)浣Y(jié)構(gòu)�。例如����,我們依次插入節(jié)點(diǎn):1,2����,3��,4,5��,6����。當(dāng)插入節(jié)點(diǎn)1時(shí),作為根節(jié)點(diǎn)����。接著插入2作為1的右孩子����,插入3作為2的右孩子�,4作為3的右孩子����,以此類推。結(jié)果BST就形成如圖八那樣的結(jié)構(gòu)�。
如果我們有技巧地排列插入值1����,2,3��,4,5,6的順序�,則BST樹將伸展得更寬,看起來更像圖六所示的結(jié)構(gòu)。理想的插入順序是:4����,2,5����,2,3,6����。這樣將4作為根節(jié)點(diǎn)�,2作為4的左孩子,5作為4的右孩子,1和3分別作為2的左孩子和右孩子�。而6則作為5的右孩子�。
既然BST的拓?fù)浣Y(jié)構(gòu)將影響搜索��、插入和刪除(下一節(jié)介紹)操作的時(shí)間復(fù)雜度����,那么以升序或降序(或近似升序降序)的方式插入數(shù)據(jù),會極大地破壞BST的效率。在本文的后面將詳細(xì)地討論��。
從BST中刪除節(jié)點(diǎn)
從BST中刪除節(jié)點(diǎn)比之插入節(jié)點(diǎn)難度更大��。因?yàn)閯h除一個(gè)非葉節(jié)點(diǎn),就必須選擇其他節(jié)點(diǎn)來填補(bǔ)因刪除節(jié)點(diǎn)所造成的樹的斷裂�。如果不選擇節(jié)點(diǎn)來填補(bǔ)這個(gè)斷裂�,那么二叉搜索樹就違背了它的特性�。例如,圖六中的二叉搜索樹。如果刪除節(jié)點(diǎn)150����,就需要某些節(jié)點(diǎn)來填補(bǔ)刪除造成的斷裂��。如果我們隨意地選擇,比如選擇92,那么就違背了BST的特性����,因?yàn)檫@個(gè)時(shí)候節(jié)點(diǎn)95和111出現(xiàn)在了92的左子樹中,而它們的值是大于92的�。
刪除節(jié)點(diǎn)算法的第一步是定位要?jiǎng)h除的節(jié)點(diǎn)�。這可以使用前面介紹的搜索算法�,因此運(yùn)行時(shí)間為log2 n。接著應(yīng)該選擇合適的節(jié)點(diǎn)來代替刪除節(jié)點(diǎn)的位置��,它共有三種情況需要考慮����,在后面的圖十有圖例說明。
情況1:如果刪除的節(jié)點(diǎn)沒有右孩子,那么就選擇它的左孩子來代替原來的節(jié)點(diǎn)。二叉搜索樹的特性保證了被刪除節(jié)點(diǎn)的左子樹必然符合二叉搜索樹的特性��。因此左子樹的值要么都大于��,要么都小于被刪除節(jié)點(diǎn)的父節(jié)點(diǎn)的值����,這取決于被刪除節(jié)點(diǎn)是左孩子還是右孩子�。因此用被刪除節(jié)點(diǎn)的左子樹來替代被刪除節(jié)點(diǎn),是完全符合二叉搜索樹的特性的����。
情況2:如果被刪除節(jié)點(diǎn)的右孩子沒有左孩子�,那么這個(gè)右孩子被用來替換被刪除節(jié)點(diǎn)��。因?yàn)楸粍h除節(jié)點(diǎn)的右孩子都大于被刪除節(jié)點(diǎn)左子樹的所有節(jié)點(diǎn)�。同時(shí)也大于或小于被刪除節(jié)點(diǎn)的父節(jié)點(diǎn)����,這同樣取決于被刪除節(jié)點(diǎn)是左孩子還是右孩子。因此��,用右孩子來替換被刪除節(jié)點(diǎn)�,符合二叉搜索樹的特性。
情況3:最后�,如果被刪除節(jié)點(diǎn)的右孩子有左孩子��,就需要用被刪除節(jié)點(diǎn)右孩子的左子樹中的最下面的節(jié)點(diǎn)來替代它,就是說��,我們用被刪除節(jié)點(diǎn)的右子樹中最小值的節(jié)點(diǎn)來替換��。
注意:我們要認(rèn)識到,在BST中��,最小值的節(jié)點(diǎn)總是在最左邊��,最大值的節(jié)點(diǎn)總是在最右邊��。
因?yàn)樘鎿Q選擇了被刪除節(jié)點(diǎn)右子樹中最小的一個(gè)節(jié)點(diǎn),這就保證了該節(jié)點(diǎn)一定大于被刪除節(jié)點(diǎn)左子樹的所有節(jié)點(diǎn)�,同時(shí)�,也保證它替代了被刪除節(jié)點(diǎn)的位置后,它的右子樹的所有節(jié)點(diǎn)值都大于它����。因此這種選擇策略符合二叉搜索樹的特性��。
圖十描述了三種情況的替換選擇方案
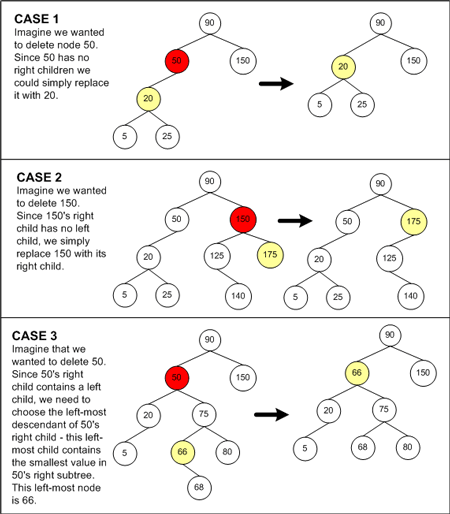
圖十
和搜索����、插入算法一樣,刪除算法的運(yùn)行時(shí)間與BST的拓?fù)浣Y(jié)構(gòu)有關(guān)��。理想狀態(tài)下����,時(shí)間復(fù)雜度為log2 n����,最壞情況下,耗費(fèi)的為線性時(shí)間��。
BST節(jié)點(diǎn)的遍歷
對于線性的連續(xù)的數(shù)組元素,采用的是單向的迭代法。從第一個(gè)元素開始,依次向后迭代每個(gè)元素��。而BST則有三種常用的遍歷方式:
1�、 前序遍歷(Perorder traversal)
2����、 中序遍歷(Inorder traversal)
3��、 后序遍歷(Postorder traversal)
當(dāng)然,這三種遍歷工作原理幾乎相似。它們都是從根節(jié)點(diǎn)開始����,然后訪問其子節(jié)點(diǎn)��。區(qū)別在于遍歷時(shí)�,訪問節(jié)點(diǎn)本身和其子節(jié)點(diǎn)的順序不同����。為幫助理解�,我們看看圖十一所示的BST樹��。(注意圖六和圖十一所示的BST樹完全相同�。

圖十一
前序遍歷
前序遍歷從當(dāng)前節(jié)點(diǎn)(節(jié)點(diǎn)c)開始�,然后訪問其左孩子��,再訪問右孩子。如果從BST樹的根節(jié)點(diǎn)c開始��,算法如下:
1�、 訪問c�。(這里所謂訪問時(shí)指輸出節(jié)點(diǎn)的值,并將節(jié)點(diǎn)添加到ArrayList中��,或者其它地方����。這取決于你遍歷BST的目的。)
2、 對c的左孩子重復(fù)第一步�;
3、 對c的右孩子重復(fù)第一步����;
設(shè)想算法的第一步打印出c的值��。以圖十一所示的BST樹為例����,以前序遍歷的方法輸出的值是什么�?是的��,我們在第一步首先輸出根節(jié)點(diǎn)的值����。然后對根的左孩子執(zhí)行第一步����,輸出50�。因?yàn)榈诙绞欠磸?fù)執(zhí)行第一步操作����,因此是對根節(jié)點(diǎn)的左孩子的左孩子訪問,輸出20����。如此重復(fù)直到樹的最左邊底層����。當(dāng)?shù)竭_(dá)節(jié)點(diǎn)5時(shí)��,輸出其值����。既然5沒有左����、右孩子,我們又回到節(jié)點(diǎn)20�,執(zhí)行第三步��。此時(shí)是對節(jié)點(diǎn)20的右孩子反復(fù)執(zhí)行第一步����,即輸出25。25沒有孩子節(jié)點(diǎn)��,又回到20�。但我們對20已經(jīng)做完了三步操作����,所以回到節(jié)點(diǎn)50。再對50執(zhí)行第三步操作,即對50的右孩子重復(fù)執(zhí)行第一步����。這個(gè)過程不斷進(jìn)行��,直到遍歷完樹的所有節(jié)點(diǎn)。最后通過前序遍歷輸出的結(jié)果如下:
90, 50, 20, 5, 25, 75, 66, 80, 150, 95, 92, 111, 175, 166, 200
可以理解��,這個(gè)算法確實(shí)有點(diǎn)讓人糊涂。或許我們來看看算法的代碼可以理清思路����。下面的代碼為BST類的PreorderTraversal()方法��,這個(gè)類在文章后面會構(gòu)建。注意這個(gè)方法調(diào)用了Node類的實(shí)例作為輸出參數(shù)。輸出的節(jié)點(diǎn)就是算法步驟中所提到的節(jié)點(diǎn)c。執(zhí)行前序遍歷就是從BST的根節(jié)點(diǎn)開始調(diào)用PreorderTraversal()方法。
protected virtual string PreorderTraversal(Node current, string separator)
{
if (current != null)
{
StringBuilder sb = new StringBuilder();
sb.Append(current.Value.ToString());
sb.Append(separator);
sb.Append(PreorderTraversal(current.Left, separator));
sb.Append(PreorderTraversal(current.Right, separator));
return sb.ToString();
}
else
return String.Empty;
}
(譯注:實(shí)際上本方法就是一個(gè)遞歸調(diào)用)
注意遍歷后的結(jié)果放到字符串中��,這個(gè)字符串時(shí)通過StringBuilder創(chuàng)建��。首先將當(dāng)前節(jié)點(diǎn)的值放到字符串中�,然后再訪問當(dāng)前節(jié)點(diǎn)的左����、右孩子��,將結(jié)果放到字符串中。
中序遍歷
中序遍歷是從當(dāng)前節(jié)點(diǎn)的左孩子開始訪問�,再訪問當(dāng)前節(jié)點(diǎn),最后是其右節(jié)點(diǎn)�。假定BST樹的根節(jié)點(diǎn)為c��,算法如下:
1����、 訪問c的左孩子��。(這里所謂訪問時(shí)指輸出節(jié)點(diǎn)的值�,并將節(jié)點(diǎn)添加到ArrayList中,或者其它地方�。這取決于你遍歷BST的目的�。)
2、 對c重復(fù)第一步�;
3�、 對c的右孩子重復(fù)第一步。
InorderTraversal()方法的代碼和PreorderTraversal()相似,只是添加當(dāng)前節(jié)點(diǎn)值到StringBuilder的操作之前,先遞歸調(diào)用方法本身��,并將當(dāng)前節(jié)點(diǎn)的左孩子作為參數(shù)傳遞��。
protected virtual string InorderTraversal
(Node current, string separator)
{
if (current != null)
{
StringBuilder sb = new StringBuilder();
sb.Append(InorderTraversal(current.Left, separator));
sb.Append(current.Value.ToString());
sb.Append(separator);
sb.Append(InorderTraversal(current.Right, separator));
return sb.ToString();
}
else
return String.Empty;
}
對圖十一所示BST樹執(zhí)行中序遍歷�,輸出結(jié)果如下:
5, 20, 25, 50, 66, 75, 80, 90, 92, 95, 111, 150, 166, 175, 200
可以看到返回的結(jié)果正好是升序排列�。
后序遍歷
后序遍歷首先從訪問當(dāng)前節(jié)點(diǎn)的左孩子開始��,然后是右孩子����,最后才是當(dāng)前節(jié)點(diǎn)本身����。假定BST樹的根節(jié)點(diǎn)為c,算法如下:
1����、 訪問c的左孩子。(這里所謂訪問時(shí)指輸出節(jié)點(diǎn)的值�,并將節(jié)點(diǎn)添加到ArrayList中,或者其它地方�。這取決于你遍歷BST的目的����。)
2��、 對c的右孩子重復(fù)第一步��;
3����、 對c重復(fù)第一步;
圖十一所示的BST樹經(jīng)后序遍歷輸出的結(jié)果為:
5, 25, 20, 66, 80, 75, 50, 92, 111, 95, 166, 200, 175, 150, 90
注意:本文提供的下載內(nèi)容包括BST和BinaryTree類的完整源代碼����,同時(shí)還包括對BST類的windows窗體的測試應(yīng)用程序��。尤其有用的是,通過Windows應(yīng)用程序,你可以看到對BST進(jìn)行前序、中序��、后序遍歷輸出的結(jié)果。
這三種遍歷的運(yùn)行時(shí)間都是線性的����。因?yàn)槊糠N遍歷都將訪問樹的每一個(gè)節(jié)點(diǎn)����,而其對每個(gè)節(jié)點(diǎn)正好訪問一次����。因此,BST樹的節(jié)點(diǎn)數(shù)成倍增加����,則遍歷的時(shí)間也將倍增��。
實(shí)現(xiàn)BST類
雖然Java的SDK包括了BST類(稱為TreeMap)�,但.Net Framework基類庫卻不包括該類。因此我們必須自己創(chuàng)建����。和二叉樹一樣��,首先要?jiǎng)?chuàng)建Node類。我們不能對普通二叉樹中的Node類進(jìn)行簡單地重用,因?yàn)?/SPAN>BST樹的節(jié)點(diǎn)是可比較的��。因此��,不僅僅是要求節(jié)點(diǎn)數(shù)據(jù)為object類型����,還要求數(shù)據(jù)為實(shí)現(xiàn)IComparable接口的類類型����。
另外,BST節(jié)點(diǎn)需要實(shí)現(xiàn)接口Icloneable����,因?yàn)槲覀儽仨氃试S開發(fā)者能夠?qū)?/SPAN>BST類進(jìn)行克隆clone(即深度拷貝)����。使Node類可克隆�,那么我們就可以通過返回根節(jié)點(diǎn)的克隆達(dá)到克隆整個(gè)BST的目的。Node類如下:
public class Node : ICloneable
{
private IComparable data;
private Node left, right;
#region Constructors
public Node() : this(null) {}
public Node(IComparable data) : this(data, null, null) {}
public Node(IComparable data, Node left, Node right)
{
this.data = data;
this.left = left;
this.right = right;
}
#endregion
#region Public Methods
public object Clone()
{
Node clone = new Node();
if (data is ICloneable)
clone.Value = (IComparable) ((ICloneable) data).Clone();
else
clone.Value = data;
if (left != null)
clone.Left = (Node) left.Clone();
if (right != null)
clone.Right = (Node) right.Clone();
return clone;
}
#endregion
#region Public Properties
public IComparable Value
{
get
{
return data;
}
set
{
data = value;
}
}
public Node Left
{
get
{
return left;
}
set
{
left = value;
}
}
public Node Right
{
get
{
return right;
}
set
{
right = value;
}
}
#endregion
}
注意BST的Node類與二叉樹的Node類有很多相似性�。唯一的區(qū)別是data的類型為Icomparable而非object類型�,而其Node類實(shí)現(xiàn)了Icloneable接口����,因此可以調(diào)用Clone()方法。
現(xiàn)在將重心放到創(chuàng)建BST類上��,它實(shí)現(xiàn)了二叉搜索樹����。在下面的幾節(jié)中����,我們會介紹這個(gè)類的每個(gè)主要方法。至于類的完整代碼����,可以點(diǎn)擊Download the BinaryTrees.msi sample file 下載源代碼��,以及測試BST類的Windows應(yīng)用程序。
搜索節(jié)點(diǎn)
BST之所以重要就是它提供得搜索算法時(shí)間復(fù)雜度遠(yuǎn)低于線性時(shí)間����。因此了解Search()方法是非常有意義的�。Search()方法接收一個(gè)IComparable類型的輸入?yún)?shù)�,同時(shí)還將調(diào)用一個(gè)私有方法SearchHelper(),傳遞BST的根節(jié)點(diǎn)和所有搜索的數(shù)據(jù)。
SearchHelper()對樹進(jìn)行遞歸調(diào)用����,如果沒有找到指定值��,返回null值,否則返回目標(biāo)節(jié)點(diǎn)。Search()方法的返回結(jié)果如果為空��,說明要查找的數(shù)據(jù)不在BST中����,否則就指向等于data值的節(jié)點(diǎn)��。
public virtual Node Search(IComparable data)
{
return SearchHelper(root, data);
}
protected virtual Node SearchHelper(Node current, IComparable data)
{
if (current == null)
return null; // node was not found
else
{
int result = current.Value.CompareTo(data);
if (result == 0)
// they are equal - we found the data
return current;
else if (result > 0)
{
// current.Value > n.Value
// therefore, if the data exists it is in current's left subtree
return SearchHelper(current.Left, data);
}
else // result < 0
{
// current.Value < n.Value
// therefore, if the data exists it is in current's right subtree
return SearchHelper(current.Right, data);
}
}
}
添加節(jié)點(diǎn)到BST
和前面創(chuàng)建的BinaryTree類不同,BST類并不提供直接訪問根的方法。通過BST的Add()方法可以添加節(jié)點(diǎn)到BST。Add()接收一個(gè)實(shí)現(xiàn)IComparable接口的實(shí)例類對象作為新節(jié)點(diǎn)的值��。然后以一種迂回的方式查找新節(jié)點(diǎn)的父節(jié)點(diǎn)��。(回想前面提到的插入新的葉節(jié)點(diǎn)的內(nèi)容)一旦父節(jié)點(diǎn)找到�,則比較新節(jié)點(diǎn)與父節(jié)點(diǎn)值的大小����,以決定新節(jié)點(diǎn)是作為父節(jié)點(diǎn)的左孩子還是右孩子��。
public virtual void Add(IComparable data)
{
// first, create a new Node
Node n = new Node(data);
int result;
// now, insert n into the tree
// trace down the tree until we hit a NULL
Node current = root, parent = null;
while (current != null)
{
result = current.Value.CompareTo(n.Value);
if (result == 0)
// they are equal - inserting a duplicate - do nothing
return;
else if (result > 0)
{
// current.Value > n.Value
// therefore, n must be added to current's left subtree
parent = current;
current = current.Left;
}
else if (result < 0)
{
// current.Value < n.Value
// therefore, n must be added to current's right subtree
parent = current;
current = current.Right;
}
}
// ok, at this point we have reached the end of the tree
count++;
if (parent == null)
// the tree was empty
root = n;
else
{
result = parent.Value.CompareTo(n.Value);
if (result > 0)
// parent.Value > n.Value
// therefore, n must be added to parent's left subtree
parent.Left = n;
else if (result < 0)
// parent.Value < n.Value
// therefore, n must be added to parent's right subtree
parent.Right = n;
}
}
Search()方法是對BST從上到下進(jìn)行遞歸操作��,而Add()方法則是使用一個(gè)簡單的循環(huán)。兩種方式殊途同歸��,但使用while循環(huán)在性能上比之遞歸更有效�。所以我們應(yīng)該認(rèn)識到BST的方法都可以用這兩種方法——遞歸或循環(huán)——其中任意一種來重寫。(個(gè)人認(rèn)為遞歸算法更易于理解����。)
注意:當(dāng)用戶試圖插入一個(gè)重復(fù)節(jié)點(diǎn)時(shí)��,Add()方法的處理方式是放棄該插入操作,你也可以根據(jù)需要修改代碼使之拋出一個(gè)異常�。
從BST中刪除節(jié)點(diǎn)
在BST的所有操作中�,刪除一個(gè)節(jié)點(diǎn)是最復(fù)雜的�。復(fù)雜度在于刪除一個(gè)節(jié)點(diǎn)必須選擇一個(gè)合適的節(jié)點(diǎn)來替代因刪除節(jié)點(diǎn)造成的斷裂。注意選擇替代節(jié)點(diǎn)必須符合二叉搜索樹的特性����。
在前面“從BST中刪除節(jié)點(diǎn)”一節(jié)中��,我們提到選擇節(jié)點(diǎn)來替代被刪除節(jié)點(diǎn)共有三種情形,這些情形在圖十中已經(jīng)有了總結(jié)����。下面我們來看看Delete()方法是怎樣來確定這三種情形的�。
public void Delete(IComparable data)
{
// find n in the tree
// trace down the tree until we hit n
Node current = root, parent = null;
int result = current.Value.CompareTo(data);
while (result != 0 && current != null)
{
if (result > 0)
{
// current.Value > n.Value
// therefore, n must be added to current's left subtree
parent = current;
current = current.Left;
}
else if (result < 0)
{
// current.Value < n.Value
// therefore, n must be added to current's right subtree
parent = current;
current = current.Right;
}
result = current.Value.CompareTo(data);
}
// if current == null, then we did not find the item to delete
if (current == null)
throw new Exception("Item to be deleted does not exist in the BST.");
// at this point current is the node to delete, and parent is its parent
count--;
// CASE 1: If current has no right child, then current's left child becomes the
// node pointed to by the parent
if (current.Right == null)
{
if (parent == null)
root = current.Left;
else
{
result = parent.Value.CompareTo(current.Value);
if (result > 0)
// parent.Value > current
// therefore, the parent's left subtree is now current's Left subtree
parent.Left = current.Left;
else if (result < 0)
// parent.Value < current.Value
// therefore, the parent's right subtree is now current's left subtree
parent.Right = current.Left;
}
}
// CASE 2: If current's right child has no left child, then current's right child replaces
// current in the tree
else if (current.Right.Left == null)
{
if (parent == null)
root = current.Right;
else
{
result = parent.Value.CompareTo(current.Value);
if (result > 0)
// parent.Value > current
// therefore, the parent's left subtree is now current's right subtree
parent.Left = current.Right;
else if (result < 0)
// parent.Value < current.Value
// therefore, the parent's right subtree is now current's right subtree
parent.Right = current.Right;
}
}
// CASE 3: If current's right child has a left child, replace current with current's
// right child's left-most node.
else
{
// we need to find the right node's left-most child
Node leftmost = current.Right.Left, lmParent = current.Right;
while (leftmost.Left != null)
{
lmParent = leftmost;
leftmost = leftmost.Left;
}
// the parent's left subtree becomes the leftmost's right subtree
lmParent.Left = leftmost.Right;
// assign leftmost's left and right to current's left and right
leftmost.Left = current.Left;
leftmost.Right = current.Right;
if (parent == null)
root = leftmost;
else
{
result = parent.Value.CompareTo(current.Value);
if (result > 0)
// parent.Value > current
// therefore, the parent's left subtree is now current's right subtree
parent.Left = leftmost;
else if (result < 0)
// parent.Value < current.Value
// therefore, the parent's right subtree is now current's right subtree
parent.Right = leftmost;
}
}
}
注意:當(dāng)沒有找到指定被刪除的節(jié)點(diǎn)時(shí)��,Delete()方法拋出一個(gè)異常����。
其他的BST方法和屬性
還有其他的BST方法和屬性在本文中沒有介紹�。我們可以下載本文附帶的完整的源代碼來仔細(xì)分析BST類。其余的方法包括:
Clear():移出BST的所有節(jié)點(diǎn)��。
Clone():克隆BST(創(chuàng)建一個(gè)深度拷貝)�。
Contains(IComparable):返回一個(gè)布爾值確定BST中是否存在其值為指定數(shù)據(jù)的節(jié)點(diǎn)�。
GetEnumerator():用中序遍歷算法對BST節(jié)點(diǎn)進(jìn)行枚舉,并返回枚舉數(shù)�。這個(gè)方法使BST可通過foreach循環(huán)迭代節(jié)點(diǎn)��。
PreorderTraversal()/InorderTraversal()/PostorderTraversal():在“遍歷BST節(jié)點(diǎn)”一節(jié)中已經(jīng)介紹。
ToString():使用BST特定的遍歷算法返回字符型的表示結(jié)果。
Count:公共的只讀屬性�,返回BST的節(jié)點(diǎn)數(shù)�。
現(xiàn)實(shí)世界的二叉搜索樹
二叉搜索樹理想的展示了對于插入�、搜索、刪除操作在時(shí)間復(fù)雜度上低于線性時(shí)間的特點(diǎn),而這種時(shí)間復(fù)雜度與BST的拓?fù)浣Y(jié)構(gòu)有關(guān)����。在“插入節(jié)點(diǎn)到BST中”一節(jié)中�,我們提到拓?fù)浣Y(jié)構(gòu)與插入節(jié)點(diǎn)的順序有關(guān)����。如果插入的數(shù)據(jù)是有序的,或者近似有序的�,都將導(dǎo)致BST樹成為一顆深而窄��,而非淺而寬的樹。而在很多現(xiàn)實(shí)情況下����,數(shù)據(jù)都處于有序或近似有序的狀態(tài)��。
BST樹的問題是很容易成為不均衡的。均衡的二叉樹是指寬度與深度之比是優(yōu)化的����。在本系列文章的下一部份����,會介紹一種自我均衡的特殊BST類����。那就是說����,不管是添加新節(jié)點(diǎn)還是刪除已有節(jié)點(diǎn)��,BST都會自動調(diào)節(jié)其拓?fù)浣Y(jié)構(gòu)來保持最佳的均衡狀態(tài)。最理想的均衡狀態(tài)��,就是插入��、搜索和刪除的時(shí)間復(fù)雜度在最壞情況下也為log2 n�。我在前面提到過Java SDK中有一個(gè)名為TreeMap的BST類��,這個(gè)類實(shí)際上就是派生于一種職能地�、自我均衡的BST樹——紅黑樹(the red-black tree)�。
在本系列文章的下一部分,我們就將介紹這種可自我均衡的BST樹����,包括紅黑樹��。重點(diǎn)介紹一種成為SkipList的數(shù)據(jù)結(jié)構(gòu)。這種結(jié)構(gòu)體現(xiàn)了自我均衡的二叉樹的性能����,同時(shí)并不需要對其拓?fù)浣Y(jié)構(gòu)進(jìn)行重構(gòu)��。
先到此為止,好好享受編程的樂趣吧!