|
|
今天做的還可以，當(dāng)然，對(duì)我來說。唯一的缺點(diǎn)是別人當(dāng)水題做的D我沒做出來。簡單的BFS，我愣是不會(huì)。哎，還是要把基礎(chǔ)打好啊。最后A掉3道，還有一道線段樹的沒有過，過些時(shí)間補(bǔ)上。我該抓緊時(shí)間復(fù)習(xí)了...  A - River Pollution
線段樹，求面積的并，很基礎(chǔ)的線段樹+離散化+掃描線，但我就是不會(huì)~
B - Middle number
今天這個(gè)是第一個(gè)過的，如果這個(gè)不過我相信后邊會(huì)更加艱難。給定一個(gè)數(shù)的序列，然后不斷的插入數(shù)字并保持遞增，最后詢問中間的數(shù)是多少。如果
數(shù)的個(gè)數(shù)是偶數(shù)，輸出中間兩個(gè)中小的。數(shù)據(jù)很大，時(shí)間是5s，我冒了個(gè)險(xiǎn)，第一次先排序，每次二分找到要插入的位置，然后順序修改后邊的序列，過了！
二分的效率啊!!我看到后邊這個(gè)題無數(shù)人TLE到死。。。這個(gè)題給了我很大信心，不然。。。
現(xiàn)在知道了，正解是用兩個(gè)堆，一個(gè)大頂堆，一個(gè)小頂堆，大頂堆只能和小頂堆元素個(gè)數(shù)相同或者正好多一個(gè)。開始時(shí)將小的一般給大頂堆，大的一半給小頂堆，插入時(shí)和堆頂元素比一下，若大于大頂堆的堆頂元素，則插給小堆，否則給了大堆。詢問時(shí)只需輸出大堆的堆頂元素就可以了。
C - Game of Stones
JL出的題，乍一看很難，但是后來才知道簡單的要命：兩個(gè)人A和B玩游戲，有兩堆石子M和N，每次兩個(gè)人都至少從兩堆中任意一堆拿至少一個(gè)石子，直到兩堆石子都為空最后一個(gè)拿的人WIN。，A總是第一個(gè)拿，給定M和N，問A能否獲勝。( 0 < M , N < 10^50 )
答案：如果M==N，A輸，否則，A贏。我考慮到奇偶上了，結(jié)果WA了5次，哎。。。
D - The longest athletic track
給定N個(gè)點(diǎn)，和一棵生成樹（N-1條邊），最后問最長的一條路是多少。
上圖的答案是80。
求樹的直徑，兩次BFS，第一次任選起點(diǎn)，則終點(diǎn)一定是直徑的一個(gè)端點(diǎn)。然后再來一次BFS就可以了。
E - Buy Car
Brent喜歡騎摩托，現(xiàn)在有N個(gè)城市，Brent 想把所有城市逛一遍，但是他怕油不夠。每升油可以跑10km，他可以在任何一個(gè)城市加油。給出M條邊，
最后問Brent的摩托的容量最小是多少，如果不能逛完所有城市，輸出-1。
簡單的最小生成樹(正是Brent講座講的~)，找出最小生成樹最小的一條邊長度為A。如果A%10==0，答案是A/10;否則答案是A/10+1;
最后排名大概是10名？(除去老隊(duì)員和admin大概是7,8名的樣子)，問題應(yīng)該不大了。嘻嘻，加油吧~ 可惡的BFS。。。一定搞定它。
這道題用到了一個(gè)我不知道的定理，Pick定理。意思是格子面上的多邊形的邊的點(diǎn)的個(gè)數(shù)on和內(nèi)部點(diǎn)的個(gè)數(shù)in的關(guān)系式Area = on / 2 + in - 1; 求Area可以用叉乘法。注意最后那個(gè)Area/=2.0。 Code：
  /**//*TOJ 1011 Area
 pick theory */
 #include<stdio.h>
#include<stdlib.h>
#include<math.h>
int px[100],py[100];
int gcd(int a,int b) {
 int temp;
  while(b!=0){
temp=b;
b=a%b;
a=temp;
 }
return a;
}
int main(void)
{
int cas,dx,dy,on,in,i,j,n;
double area;
scanf("%d",&cas);
for(j=1;j<=cas;j++){
scanf("%d",&n);
px[0]=py[0]=dx=dy=area=on=0;
for(i=1;i<=n;i++){
scanf("%d%d",&dx,&dy);
on+=gcd(abs(dx),abs(dy));
px[i]=px[i-1]+dx;
py[i]=py[i-1]+dy;
area+=(px[i-1]*py[i]-px[i]*py[i-1]);
}
area=area/2.0;
in=area+1-on/2;
printf("Scenario #%d:\n%d %d %.1lf\n\n",j,in,on,area);
}
}
簡單的DP，大意是給出N場比賽球隊(duì)的輸，平，贏的場數(shù)，最后問M場比賽至少拿S分的概率。贏一場3分，平一場1分，輸0分。 dp[i][j]表示 i 場比賽得 j 分的概率。則有轉(zhuǎn)移方程dp[i][j]=dp[i-1][j-3]*r1+dp[i-1][j-1]*r2+dp[i-1][j]*r3;(r1,r2,r3分別表示每一場贏，平，輸?shù)母怕? Code：
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
double dp[90][270];
int main()
{
int i,j,k,n,m;
double r1,r2,r3,sum;
while(scanf("%d%d",&n,&m),n+m){
scanf("%d%d%d",&i,&j,&k);
r1=i*1.0/(i+j+k);
r2=j*1.0/(i+j+k);
r3=k*1.0/(i+j+k);
memset(dp,0,sizeof(dp));
dp[1][0]=r3;dp[1][1]=r2;dp[1][3]=r1;
for(i=2;i<=n;i++)
for(j=0;j<=3*i;j++){
if(j<=0) // 防止數(shù)組下標(biāo)出現(xiàn)負(fù)數(shù)
dp[i][j]=dp[i-1][j]*r3;
else if(j<=1) //同上
dp[i][j]=dp[i-1][j]*r3+dp[i-1][j-1]*r2;
else
dp[i][j]=dp[i-1][j]*r3+dp[i-1][j-1]*r2+dp[i-1][j-3]*r1;
}
sum=0.0;
for(i=m;i<=3*n;i++)
sum+=dp[n][i];
printf("%.1lf\n",sum*100);
}
}
一個(gè)結(jié)論很簡單的問題，對(duì)于任意兩個(gè)數(shù)a,b(a,b>=2)
1)如果gcd (a,b)==1，則最大的不能由a，b線性表示的數(shù)為a*b-a-b；
2)否則這個(gè)數(shù)時(shí)無窮大
至于證明，期待大牛給出，我還是不懂，一開始往拓展歐幾里得想的，但后來也沒什么結(jié)論。
哪位神牛知道證明給點(diǎn)提示，不勝感謝~
Code略去(太水了)
一個(gè)求逆序?qū)Φ念}，N個(gè)數(shù)，N<=500000，問排成遞增序列需要相鄰的數(shù)交換多少次。一開始沒有仔細(xì)看題，上來就做，后來才發(fā)現(xiàn)數(shù)的范圍是999999999。因?yàn)樽疃?00000個(gè)數(shù)，所以數(shù)和數(shù)之間的間隔很大，可以處理一下，使數(shù)的間隔變小，然后使用樹狀數(shù)組統(tǒng)計(jì)某個(gè)數(shù)前邊的比它大的數(shù)的個(gè)數(shù)。將所有的數(shù)放到一個(gè)結(jié)構(gòu)體里，稱作num，并增加一個(gè)成員id，然后按num遞增排列，再另開一個(gè)數(shù)組給每個(gè)數(shù)重新編號(hào)，使數(shù)的范圍都在N以內(nèi)。然后就可以很自然的用樹狀數(shù)組做了。時(shí)間500ms。據(jù)說歸并排序比這個(gè)要快。 Code：
1 #include<iostream>
2 #include<algorithm>
3 #define M 500001
4 using namespace std;
5 int c[M],aa[M],n; //aa數(shù)組為排序后重新編號(hào)用
6 struct digit
7 {
8 int num,id;
9 }a[M]; //num為數(shù)的大小
10 bool cmp(digit a,digit b){
11 return a.num<b.num;
12 }
13 int lowbit(int t){
14 return t&(t^(t-1));
15 }
16 int sum(int t){
17 int total=0;
18 while(t>0){
19 total+=c[t];
20 t-=lowbit(t);
21 }
22 return total;
23 }
24 void update(int t,int key){
25 while(t<=n){
26 c[t]+=key;
27 t+=lowbit(t);
28 }
29 }
30 int main()
31 {
32 int i,j;
33 long long ans;
34 while(scanf("%d",&n),n){
35 memset(c,0,sizeof(c));
36 ans=0;
37 for(i=1;i<=n;i++){
38 scanf("%d",&a[i].num);
39 a[i].id=i;
40 }
41 sort(a+1,a+n+1,cmp);
42 aa[a[1].id]=1; //最小的數(shù)編號(hào)為1
43 for(i=2;i<=n;++i){
44 if(a[a[i].id].num!=a[a[i-1].id].num) //如果前后兩個(gè)數(shù)不等，則編號(hào)為下標(biāo)
45 aa[a[i].id]=i;
46 else
47 aa[a[i].id]=aa[a[i-1].id]; //否則編號(hào)與前一個(gè)相同
48 }
49 //for(i=1;i<=n;i++) printf("%d ",aa[i]);
50 for(i=1;i<=n;++i){
51 update(aa[i],1);
52 ans+=(sum(n)-sum(aa[i])); //每次累加該數(shù)前邊比它大的數(shù)的個(gè)數(shù)
53 }
54 printf("%lld\n",ans);
55 }
56 }
簡單的二維樹狀數(shù)組，求一個(gè)矩形區(qū)域內(nèi)的和，因?yàn)橐S時(shí)增減，而且可能減的數(shù)比原來都大，所以需要保留原來的數(shù)組。 在求矩形區(qū)域和的時(shí)候，只要用最大的矩形減去兩個(gè)小的，再加上那個(gè)多減的最小的，就OK了。1y~~ Code：
1 #include<iostream>
2 #define M 1300
3 int c[M][M],a[M][M],n;
4 int lowbit(int t){
5 return t&(t^(t-1));
6 }
7 int sum(int p,int q){
8 int x=p,y,total=0;
9 while(x>0){
10 y=q;
11 while(y>0){
12 total+=c[x][y];
13 y-=lowbit(y);
14 }
15 x-=lowbit(x);
16 }
17 return total;
18 }
19 void modify(int p,int q,int key){
20 int x=p,y;
21 while(x<=n){
22 y=q;
23 while(y<=n){
24 c[x][y]+=key;
25 y+=lowbit(y);
26 }
27 x+=lowbit(x);
28 }
29 }
30 int main()
31 {
32 int i,j,k,jj,kk,m,order,ans;
33 scanf("%d%d",&i,&n);
34 memset(c,0,sizeof(c));
35 memset(a,0,sizeof(a));
36 while(scanf("%d",&order)!=EOF){
37 if(order==3) break;
38 else if(order==1){
39 scanf("%d%d%d",&j,&k,&m);
40 ++j; ++k;
41 if(m<0&&m*(-1)>a[j][k]){
42 m=(-1)*a[j][k];
43 modify(j,k,m);
44 a[j][k]=0;
45 }
46 else{
47 modify(j,k,m);
48 a[j][k]+=m;
49 }
50 }
51 else if(order==2){
52 scanf("%d%d%d%d",&j,&jj,&k,&kk);
53 ++j; ++jj; ++k; ++kk;
54 //printf("%d ",sum(n,n));
55 ans=sum(k,kk)+sum(j-1,jj-1)-sum(k,jj-1)-sum(j-1,kk);
56 printf("%d\n",ans);
57 }
58 }
59 }
今天聯(lián)系樹狀數(shù)組，但是我發(fā)現(xiàn)我真的很笨，做了好幾道了還是不熟。這個(gè)題和前邊的也沒什么分別，是說每個(gè)牛有一個(gè)區(qū)間[s,e],兩個(gè)牛[s1,e1], [s2,e2]，當(dāng)s1<=s2并且e1>=e2并且e1-s1>e2-s2時(shí)，我們說牛1比牛2強(qiáng)，給N個(gè)牛的區(qū)間，對(duì)于每個(gè)牛，輸出比這個(gè)牛強(qiáng)的牛的個(gè)數(shù)。 還是需要預(yù)處理，先對(duì)每個(gè)牛的e進(jìn)行降序排序，e相同時(shí)對(duì)s進(jìn)行升序排列，這樣循環(huán)時(shí)可以保證后邊的牛絕對(duì)不比前邊的牛強(qiáng)。在循環(huán)時(shí)，只需找出比當(dāng)前牛s小的牛的個(gè)數(shù)。如果遇到特殊情況，即兩個(gè)牛區(qū)間完全一樣，賦值就可以了。哎，加油吧~ Code：
1 #include<iostream>
2 #include<algorithm>
3 #include<map>
4 #define MAX 100002
5 using namespace std;
6 int c[MAX],ans[MAX],n,imax;
7 struct cow
8 {
9 int l,r,id;
10 }a[MAX];
11 bool cmp(cow a,cow b){
12 if(a.r==b.r) //如果兩個(gè)牛區(qū)間右邊界相同，按左邊界的升序排列
13 return a.l<b.l;
14 return a.r>b.r; //按右邊界的降序排列
15 }
16 int lowbit(int t){
17 return t&(t^(t-1));
18 }
19 int sum(int t){
20 int total=0;
21 while(t>0){
22 total+=c[t];
23 t-=lowbit(t);
24 }
25 return total;
26 }
27 void modify(int posi,int key){
28 while(posi<=imax){
29 c[posi]+=key;
30 posi+=lowbit(posi);
31 }
32 }
33 int main()
34 {
35 int i,j,k,n;
36 while(scanf("%d",&n),n){
37 memset(c,0,sizeof(c));
38 imax=0;
39 for(i=1;i<=n;i++){
40 scanf("%d%d",&a[i].l,&a[i].r);
41 a[i].id=i; //每個(gè)牛有個(gè)id防止排序完順序變亂
42 ++a[i].l; ++a[i].r;
43 if(imax<a[i].l) imax=a[i].l; //用imax表示右邊界最大值，即求和時(shí)的邊界
44 }
45 sort(a+1,a+n+1,cmp);
46 for(i=1;i<=n;++i){
47 if(i==1){
48 ans[a[i].id]=sum(a[i].l); //這里注意是ans[a[i].id]而不是ans[i]
49 modify(a[i].l,1);
50 }
51 else{
52 if(a[i].l==a[i-1].l&&a[i].r==a[i-1].r) //如果兩個(gè)牛完全相同，直接賦值
53 ans[a[i].id]=ans[a[i-1].id];
54 else
55 ans[a[i].id]=sum(a[i].l); //否則找出左邊界l比這個(gè)牛小的
56 modify(a[i].l,1);
57 }
58 }
59 for(i=1;i<n;++i)
60 printf("%d ",ans[i]);
61 printf("%d\n",ans[i]);
62 }
63 }
64
大意是N個(gè)星星，規(guī)定每個(gè)星星的等級(jí)為在它左下方星星的數(shù)量（包括某個(gè)坐標(biāo)相等），N范圍是15000，輸入按y坐標(biāo)的升序給出，如果兩個(gè)星星y坐標(biāo)相等，按x坐標(biāo)升序給出。 用樹狀數(shù)組，不用管y坐標(biāo)（因?yàn)橐呀?jīng)是升序，后邊的星星不影響前邊星星的等級(jí)），用sum(n)來統(tǒng)計(jì)x坐標(biāo)為n以前的星星個(gè)數(shù)，但是千萬注意樹狀數(shù)組需要數(shù)組以1為首項(xiàng)，由于坐標(biāo)有0，所以每次需要給x坐標(biāo)+1。另外，通過這個(gè)題，我發(fā)現(xiàn)++i果然比i++快。兩者一個(gè)420ms，一個(gè)360ms。還是差不少的，以后盡量用++i了:D Code：
1 #include<stdio.h>
2 #include<string.h>
3 #define M 32006 //坐標(biāo)范圍是32000
4 int c[M],ans[M/2]; //c為樹狀數(shù)組，ans[i]表示level為i的星星個(gè)數(shù)
5 int lowbit(int t){
6 return t&(t^(t-1));
7 }
8 int sum(int m){
9 int total=0;
10 while(m>0){
11 total+=c[m];
12 m-=lowbit(m);
13 }
14 return total;
15 }
16 void modify(int position){
17 while(position<=32002){
18 ++c[position];
19 position+=lowbit(position);
20 }
21 }
22 int main()
23 {
24 int x,y,i,j,n;
25 scanf("%d",&n);
26 j=n;
27 memset(c,0,sizeof(c));
28 memset(ans,0,sizeof(ans));
29 while(n--){
30 scanf("%d%d",&x,&y);
31 ++ans[sum(x+1)];
32 modify(x+1);
33 }
34 for(i=0;i<j;++i)
35 printf("%d\n",ans[i]);
36 }
這道題和那道Star如出一轍，可我還是做了很長時(shí)間 ...太菜了...有K條連接?xùn)|西兩個(gè)城市的路，東西方向每個(gè)城市都有一個(gè)編號(hào)M,N，從北到南，最后問共有多少個(gè)十字路都，即有多少個(gè)交點(diǎn)。 先預(yù)處理，用結(jié)構(gòu)體表示每條邊，對(duì)結(jié)構(gòu)體按N進(jìn)行從小到大的排序，如果N相同，按M從小到大排序。接下來就和Star一樣了，唯一不同的是Star那道題是每次求出當(dāng)前星星前邊的個(gè)數(shù)，而這個(gè)是求當(dāng)前點(diǎn)后邊的個(gè)數(shù)。用c[]表示樹狀數(shù)組，sum(n)求出的是N編號(hào)小于等于n的city的個(gè)數(shù)，只需每次拿出一個(gè)city，求出N編號(hào)大于它的city的個(gè)數(shù)，然后更新數(shù)組就可以了。 關(guān)鍵代碼：
1 long long ans=0;
2 for(i=1;i<=K;i++){ //K表示邊的個(gè)數(shù)
3 ans+=sum(max)-sum(a[i].east); //east即為N編號(hào)
4 modify(a[i].east,1); //將a[i].east插入到當(dāng)前數(shù)組
5 }
6
解決了這一步，其余就是套路了，很簡單。 Code：
1 #include<iostream>
2 #include<algorithm>
3 #define MAX 10005 //最大的city個(gè)數(shù)
4 using namespace std;
5 int c[MAX],n,N,M,K,omax;
6 struct road
7 {
8 int west,east;
9 }a[MAX*MAX]; //MAX*MAX為最多的邊的個(gè)數(shù)
10 bool cmp(road a,road b){
11 if(a.west==b.west)
12 return a.east<b.east;
13 return a.west<b.west;
14 }
15 int lowbit(int t){
16 return t&(t^(t-1));
17 }
18 int sum(int t){
19 int total=0;
20 while(t>0){
21 total+=c[t];
22 t-=lowbit(t);
23 }
24 return total;
25 }
26 void modify(int posi,int key){
27 while(posi<=omax){
28 c[posi]+=key;
29 posi+=lowbit(posi);
30 }
31 }
32 int main()
33 {
34 int i,j,k,m,cas;
35 long long ans;
36 scanf("%d",&cas);
37 for(i=1;i<=cas;++i){
38 omax=0; //用omax表示所有east的最大值，以確定求和區(qū)間
39 memset(c,0,sizeof(c));
40 scanf("%d%d%d",&N,&M,&K);
41 for(j=1;j<=K;++j){
42 scanf("%d%d",&a[j].east,&a[j].west);
43 if(a[j].east>omax)
44 omax=a[j].east;
45 }
46 sort(a+1,a+1+K,cmp);
47 ans=0;
48 for(j=1;j<=K;++j){ //key code
49 ans+=(sum(omax)-sum(a[j].east));
50 modify(a[j].east,1);
51 }
52 printf("Test case %d: %lld\n",i,ans);
53 }
54 }
55
TOJ有道題，大意是有N個(gè)位置，每個(gè)位置有若干瓶子，Mike很淘氣，他每次會(huì)增加或減少位置i的瓶子數(shù)，然后有M次詢問，求位置A到B的瓶子數(shù)的和。最開始，我一直用最直觀的做法，但是由于是O(n)的復(fù)雜度，所以一直超時(shí)。今天看了BIT的相關(guān)東西，才發(fā)現(xiàn)那個(gè)題其實(shí)是典型的BIT題目，而且是最基礎(chǔ)的，但是就和RMQ問題一樣，高效的算法背后深刻的數(shù)學(xué)理論還是不能很透徹的理解，這個(gè)只有靠以后熟練的慢慢來了：D
先來看一下樹狀數(shù)組的概念：樹狀數(shù)組是一種靜態(tài)樹狀數(shù)據(jù)結(jié)構(gòu)，它的首要作用是維護(hù)前綴和，即改變數(shù)組中某一元素a[i]的值，若要詢問前N項(xiàng)的和，樹狀數(shù)組便可完美解決。時(shí)間復(fù)雜度O(logn)。
先來直觀看一下樹狀數(shù)組的結(jié)構(gòu)（圖片來自http://fqq11679.blog.hexun.com/21722866_d.html#）
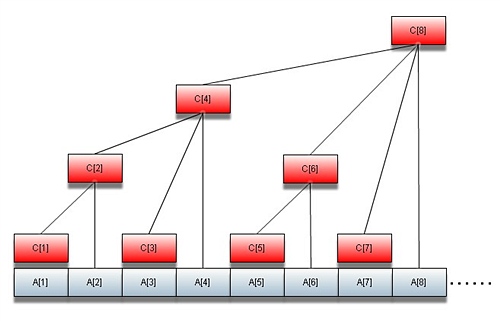
在上圖中，紅色的數(shù)組c[]便是樹狀數(shù)組。改變數(shù)組a的某一個(gè)元素i，則需要相應(yīng)的改變數(shù)組c，若要詢問前N項(xiàng)和，只需累加相應(yīng)的c，而這當(dāng)中一個(gè)核心的問題便是相應(yīng)的數(shù)組c的下標(biāo)問題。可以用位操作lowbit解決。c[i]=a[i-2^k+1]到a[i]的和，k是指i用二進(jìn)制表示時(shí)末位0的個(gè)數(shù)，即將i表示成冪方和后最小的指數(shù)。利用位運(yùn)算，我們可以得知2^k=i&(i^(i-1));
相應(yīng)的代碼為：
1 int lowbit(int n)
2 {
3 return n&(n^(n-1));
4 }
這樣，當(dāng)a[i]改變時(shí)，我們只需從c[i]開始一直向上回溯，改變路上相應(yīng)的數(shù)組c的值，若要求前N項(xiàng)和，只需求N以前所有最大子樹c[]的和。然后我們來看相應(yīng)下標(biāo)的操作：
修改a[i],則修改一路的父節(jié)點(diǎn)c[p], p=i-bit(i);
若要前i項(xiàng)求和，只需一路找子節(jié)點(diǎn)c[p], p=i-lowbit(i);
求前N項(xiàng)和：
1 int sum(int n)
2 {
3 int total=0;
4 while(n>0){
5 total+=c[n];
6 n-=lowbit(n);
7 }
8 return total;
9 }
TOJ 3505 Naughty mike Code：
1 /*TOJ 3505 Naughty mike*/
2 #include<stdio.h> //注意在使用樹狀數(shù)組時(shí)下標(biāo)一定不能從0開始
3 #include<string.h>
4 #define M 100002
5 int a[M],n;
6 int c[M];
7 int lowbit(int t) //關(guān)鍵的位操作確定數(shù)組下標(biāo)
8 {
9 return t&(t^(t-1));
10 }
11 int sum(int end) //求前end項(xiàng)和的函數(shù)，通過不斷累加最大子樹得到
12 {
13 int i;
14 int total=0;
15 while(end>0){
16 total+=c[end];
17 end-=lowbit(end);
18 }
19 return total;
20 }
21 void modify(int t,int key) //對(duì)數(shù)組某一項(xiàng)進(jìn)行修改時(shí)，只需沿該項(xiàng)一直向上回溯修改相應(yīng)的數(shù)組c
22 {
23 while(t<=n){
24 c[t]+=key;
25 t+=lowbit(t);
26 }
27 }
28 int main()
29 {
30 int i,j,k,m,cas;
31 char e[50];
32 scanf("%d",&cas);
33 while(cas--){
34 scanf("%d",&n);
35 memset(c,0,sizeof(c));
36 for(i=1;i<=n;i++){
37 scanf("%d",&a[i]);
38 modify(i,a[i]);
39 }
40 scanf("%d",&m);
41 while(m--){
42 scanf("%s%d%d",e,&i,&j);
43 if(e[0]=='A'){
44 modify(i,j);
45 a[i]+=j;
46 }
47 else if(e[0]=='D'){
48 if(j>=a[i]) j=(-1)*a[i]; //由于可能刪除的比現(xiàn)有的還多，需要分開考慮
49 else j*=(-1);
50 modify(i,j);
51 a[i]+=j;
52 }
53 else
54 printf("%d\n",sum(j)-sum(i-1)); //區(qū)間[i,j]的和
55 }
56 }
57 }
58
|