文章作者：yx_th000 文章來源：Cherish_yimi (http://www.cnblogs.com/cherish_yimi/) 轉載請注明，謝謝合作。
    
    昨天和今天學習了并查集和trie樹，并練習了三道入門題目，理解更為深刻，覺得有必要總結一下，這其中的內容定義之類的是取自網絡，操作的說明解釋及程序的注釋部分為個人理解。

    并查集學習：

l         并查集：(union-find sets)

一種簡單的用途廣泛的集合. 并查集是若干個不相交集合，能夠實現較快的合并和判斷元素所在集合的操作，應用很多，如其求無向圖的連通分量個數等。最完美的應用當屬：實現Kruskar算法求最小生成樹。

l         并查集的精髓（即它的三種操作，結合實現代碼模板進行理解）：

1、Make_Set(x) 把每一個元素初始化為一個集合

初始化后每一個元素的父親節點是它本身，每一個元素的祖先節點也是它本身（也可以根據情況而變）。

2、Find_Set(x) 查找一個元素所在的集合

查找一個元素所在的集合，其精髓是找到這個元素所在集合的祖先！這個才是并查集判斷和合并的最終依據。
判斷兩個元素是否屬于同一集合，只要看他們所在集合的祖先是否相同即可。
合并兩個集合，也是使一個集合的祖先成為另一個集合的祖先，具體見示意圖

3、Union(x,y) 合并x,y所在的兩個集合

合并兩個不相交集合操作很簡單：
利用Find_Set找到其中兩個集合的祖先，將一個集合的祖先指向另一個集合的祖先。如圖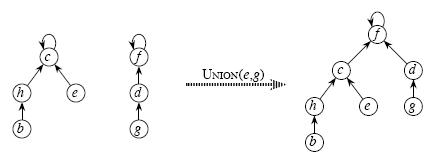

l         并查集的優化

1、Find_Set(x)時 路徑壓縮
尋找祖先時我們一般采用遞歸查找，但是當元素很多亦或是整棵樹變為一條鏈時，每次Find_Set(x)都是O(n)的復雜度，有沒有辦法減小這個復雜度呢？
答案是肯定的，這就是路徑壓縮，即當我們經過"遞推"找到祖先節點后，"回溯"的時候順便將它的子孫節點都直接指向祖先，這樣以后再次Find_Set(x)時復雜度就變成O(1)了，如下圖所示；可見，路徑壓縮方便了以后的查找。

2、Union(x,y)時 按秩合并
即合并的時候將元素少的集合合并到元素多的集合中，這樣合并之后樹的高度會相對較小。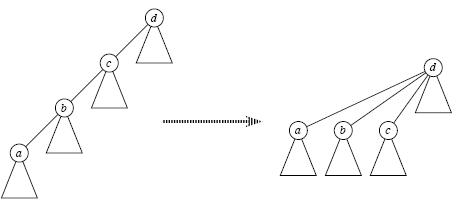

l         主要代碼實現

 1int father[MAX];   /* father[x]表示x的父節點*/
 2int rank[MAX];     /* rank[x]表示x的秩*/
 3
 4
 5/* 初始化集合*/
 6void Make_Set(int x)
 7{
 8    father[x] = x; //根據實際情況指定的父節點可變化
 9    rank[x] = 0;   //根據實際情況初始化秩也有所變化
10}
11
12
13/* 查找x元素所在的集合,回溯時壓縮路徑*/
14int Find_Set(int x)
15{
16    if (x != father[x])
17    {
18        father[x] = Find_Set(father[x]); //這個回溯時的壓縮路徑是精華
19    }
20    return father[x];
21}
22
23
24/* 
25   按秩合并x,y所在的集合
26   下面的那個if else結構不是絕對的，具體根據情況變化
27   但是，宗旨是不變的即，按秩合并，實時更新秩。
28*/
29void Union(int x, int y)
30{
31    x = Find_Set(x);
32    y = Find_Set(y);
33    if (x == y) return;
34    if (rank[x] > rank[y]) 
35    {
36        father[y] = x;
37    }
38    else
39    {
40        if (rank[x] == rank[y])
41        {
42            rank[y]++;
43        }
44        father[x] = y;
45    }
46}
47

注：學習并查集時非常感謝Slyar提供的資料，這里注明鏈接：http://www.slyar.com/blog/
另外，我認為寫并查集時涉及到的路徑壓縮，最好用遞歸，一方面代碼的可讀性非常好，另一方面，可以更直觀的理解路徑壓縮時在回溯時完成的巧妙。