亚洲午夜久久久影院伊人,久久99国产精品99久久,精品久久久久久国产牛牛app

維基百科，自由的百科全書

紅黑樹是一種自平衡二叉查找樹，是在計算機科學(xué)中用到的一種數(shù)據(jù)結(jié)構(gòu)，典型的用途是實現(xiàn)關(guān)聯(lián)數(shù)組。它是在1972年由 Robert Sedgewick 于1978年寫的一篇論文中獲得的。它是復(fù)雜的，但它的操作有著良好的最壞情況運行時間，并且在實踐中是高效的: 它可以在O(log n)時間內(nèi)做查找，插入和刪除，這里的n是樹中元素的數(shù)目。

[編輯]用途和好處

紅黑樹和AVL樹一樣都對插入時間、刪除時間和查找時間提供了最好可能的最壞情況擔(dān)保。這不只是使它們在時間敏感的應(yīng)用如實時應(yīng)用(real time application)中有價值，而且使它們有在提供最壞情況擔(dān)保的其他數(shù)據(jù)結(jié)構(gòu)中作為建造板塊的價值；例如，在計算幾何中使用的很多數(shù)據(jù)結(jié)構(gòu)都可以基于紅黑樹。

紅黑樹在函數(shù)式編程中也特別有用，在這里它們是最常用的持久數(shù)據(jù)結(jié)構(gòu)之一，它們用來構(gòu)造關(guān)聯(lián)數(shù)組和集合，在突變之后它們能保持為以前的版本。除了O(log n)的時間之外，紅黑樹的持久版本對每次插入或刪除需要O(log n)的空間。

紅黑樹是 2-3-4樹的一種等同。換句話說，對于每個 2-3-4 樹，都存在至少一個數(shù)據(jù)元素是同樣次序的紅黑樹。在 2-3-4 樹上的插入和刪除操作也等同于在紅黑樹中顏色翻轉(zhuǎn)和旋轉(zhuǎn)。這使得 2-3-4 樹成為理解紅黑樹背后的邏輯的重要工具，這也是很多介紹算法的教科書在紅黑樹之前介紹 2-3-4 樹的原因，盡管 2-3-4 樹在實踐中不經(jīng)常使用。

[編輯]性質(zhì)

紅黑樹是每個節(jié)點都帶有顏色屬性的二叉查找樹，顏色或紅色或黑色。在二叉查找樹強制一般要求以外，對于任何有效的紅黑樹我們增加了如下的額外要求:

性質(zhì)1. 節(jié)點是紅色或黑色。

性質(zhì)2. 根是黑色。

性質(zhì)3. 所有葉子都是黑色（葉子是NIL節(jié)點）。

性質(zhì)4. 每個紅色節(jié)點的兩個子節(jié)點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續(xù)的紅色節(jié)點)

性質(zhì)5. 從任一節(jié)點到其每個葉子的所有簡單路徑都包含相同數(shù)目的黑色節(jié)點。

這些約束強制了紅黑樹的關(guān)鍵性質(zhì): 從根到葉子的最長的可能路徑不多于最短的可能路徑的兩倍長。結(jié)果是這個樹大致上是平衡的。因為操作比如插入、刪除和查找某個值的最壞情況時間都要求與樹的高度成比例，這個在高度上的理論上限允許紅黑樹在最壞情況下都是高效的，而不同于普通的二叉查找樹。

要知道為什么這些特性確保了這個結(jié)果，注意到屬性4導(dǎo)致了路徑不能有兩個毗連的紅色節(jié)點就足夠了。最短的可能路徑都是黑色節(jié)點，最長的可能路徑有交替的紅色和黑色節(jié)點。因為根據(jù)屬性5所有最長的路徑都有相同數(shù)目的黑色節(jié)點，這就表明了沒有路徑能多于任何其他路徑的兩倍長。

在很多樹數(shù)據(jù)結(jié)構(gòu)的表示中，一個節(jié)點有可能只有一個子節(jié)點，而葉子節(jié)點包含數(shù)據(jù)。用這種范例表示紅黑樹是可能的，但是這會改變一些屬性并使算法復(fù)雜。為此，本文中我們使用 "nil 葉子" 或"空(null)葉子"，如上圖所示，它不包含數(shù)據(jù)而只充當(dāng)樹在此結(jié)束的指示。這些節(jié)點在繪圖中經(jīng)常被省略，導(dǎo)致了這些樹好像同上述原則相矛盾，而實際上不是這樣。與此有關(guān)的結(jié)論是所有節(jié)點都有兩個子節(jié)點，盡管其中的一個或兩個可能是空葉子。

[編輯]操作

因為每一個紅黑樹也是一個特化的二叉查找樹，因此紅黑樹上的只讀操作與普通二叉查找樹上的只讀操作相同。然而，在紅黑樹上進行插入操作和刪除操作會導(dǎo)致不再符合紅黑樹的性質(zhì)。恢復(fù)紅黑樹的屬性需要少量(O(log n))的顏色變更(實際是非常快速的)和不超過三次樹旋轉(zhuǎn)(對于插入操作是兩次)。雖然插入和刪除很復(fù)雜，但操作時間仍可以保持為 O(log n) 次。

[編輯]插入

我們首先以二叉查找樹的方法增加節(jié)點并標(biāo)記它為紅色。（如果設(shè)為黑色，就會導(dǎo)致根到葉子的路徑上有一條路上，多一個額外的黑節(jié)點，這個是很難調(diào)整的。但是設(shè)為紅色節(jié)點后，可能會導(dǎo)致出現(xiàn)兩個連續(xù)紅色節(jié)點的沖突，那么可以通過顏色調(diào)換（color flips）和樹旋轉(zhuǎn)來調(diào)整。）下面要進行什么操作取決于其他臨近節(jié)點的顏色。同人類的家族樹中一樣，我們將使用術(shù)語叔父節(jié)點來指一個節(jié)點的父節(jié)點的兄弟節(jié)點。注意:

性質(zhì)1^[1]和性質(zhì)3^[2]總是保持著。
性質(zhì)4^[3]只在增加紅色節(jié)點、重繪黑色節(jié)點為紅色，或做旋轉(zhuǎn)時受到威脅。
性質(zhì)5^[4]只在增加黑色節(jié)點、重繪紅色節(jié)點為黑色，或做旋轉(zhuǎn)時受到威脅。

在下面的示意圖中，將要插入的節(jié)點標(biāo)為N，N的父節(jié)點標(biāo)為P，N的祖父節(jié)點標(biāo)為G，N的叔父節(jié)點標(biāo)為U。在圖中展示的任何顏色要么是由它所處情形所作的假定，要么是這些假定所暗含 (imply) 的。

對于每一種情況，我們將使用 C 示例代碼來展示。通過下列函數(shù)，可以找到一個節(jié)點的叔父和祖父節(jié)點:

 node grandparent(node n) {
     return n->parent->parent;
 }
 
 node uncle(node n) {
     if (n->parent == grandparent(n)->left)
         return grandparent(n)->right;
     else
         return grandparent(n)->left;
 }

情形1: 新節(jié)點N位于樹的根上，沒有父節(jié)點。在這種情形下，我們把它重繪為黑色以滿足性質(zhì)2^[5]。因為它在每個路徑上對黑節(jié)點數(shù)目增加一，性質(zhì)5^[4]符合。

 void insert_case1(node n) {
     if (n->parent == NULL)
         n->color = BLACK;
     else
         insert_case2(n);
 }

情形2: 新節(jié)點的父節(jié)點P是黑色，所以性質(zhì)4^[3]沒有失效（新節(jié)點是紅色的）。在這種情形下，樹仍是有效的。性質(zhì)5^[4]受到威脅，因為新節(jié)點N有兩個黑色葉子兒子；但是由于新節(jié)點N是紅色，通過它的每個子節(jié)點的路徑就都有同通過它所取代的黑色的葉子的路徑同樣數(shù)目的黑色節(jié)點，所以這個性質(zhì)依然滿足。

 void insert_case2(node n) {
     if (n->parent->color == BLACK)
         return; /* 樹仍舊有效 */
     else
         insert_case3(n);
 }

注意: 在下列情形下我們假定新節(jié)點有祖父節(jié)點，因為父節(jié)點是紅色；并且如果它是根，它就應(yīng)當(dāng)是黑色。所以新節(jié)點總有一個叔父節(jié)點，盡管在情形4和5下它可能是葉子。

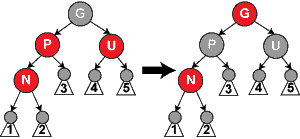
情形3: 如果父節(jié)點P和叔父節(jié)點U二者都是紅色，(此時新插入節(jié)點N做為P的左子節(jié)點或右子節(jié)點都屬于情形3,這里右圖僅顯示N做為P左子的情形)則我們可以將它們兩個重繪為黑色并重繪祖父節(jié)點G為紅色(用來保持性質(zhì)5^[4])。現(xiàn)在我們的新節(jié)點N有了一個黑色的父節(jié)點P。因為通過父節(jié)點P或叔父節(jié)點U的任何路徑都必定通過祖父節(jié)點G，在這些路徑上的黑節(jié)點數(shù)目沒有改變。但是，紅色的祖父節(jié)點G的父節(jié)點也有可能是紅色的，這就違反了性質(zhì)4^[3]。為了解決這個問題，我們在祖父節(jié)點G上遞歸地進行情形1的整個過程。（把G當(dāng)成是新加入的節(jié)點進行各種情況的檢查）

 void insert_case3(node n) {
     if (uncle(n) != NULL && uncle(n)->color == RED) {
         n->parent->color = BLACK;
         uncle(n)->color = BLACK;
         grandparent(n)->color = RED;
         insert_case1(grandparent(n));
     }
     else
         insert_case4(n);
 }

注意: 在余下的情形下，我們假定父節(jié)點P 是其父親G 的左子節(jié)點。如果它是右子節(jié)點，情形4和情形5中的左和右應(yīng)當(dāng)對調(diào)。

說明: 情形4是將是將現(xiàn)有情況轉(zhuǎn)化為情形5。情形5的問題本質(zhì)上是有連續(xù)的紅色結(jié)點，樹不再等高（不再平衡），故需翻轉(zhuǎn)以保持平衡。

情形4: 父節(jié)點P是紅色而叔父節(jié)點U是黑色或缺少; 還有，新節(jié)點N是其父節(jié)點P的右子節(jié)點，而父節(jié)點P又是其父節(jié)點的左子節(jié)點。在這種情形下，我們進行一次左旋轉(zhuǎn)調(diào)換新節(jié)點和其父節(jié)點的角色; 接著，我們按情形5處理以前的父節(jié)點P。這導(dǎo)致某些路徑通過它們以前不通過的新節(jié)點N或父節(jié)點P中的一個，但是這兩個節(jié)點都是紅色的，所以性質(zhì)5^[4]沒有失效。

 void insert_case4(node n) {
     if (n == n->parent->right && n->parent == grandparent(n)->left) {
         rotate_left(n->parent);
         n = n->left;
     } else if (n == n->parent->left && n->parent == grandparent(n)->right) {
         rotate_right(n->parent);
         n = n->right;
     }
     insert_case5(n);
 }

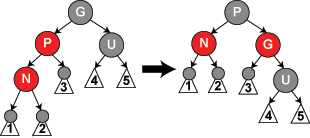
情形5: 父節(jié)點P是紅色而叔父節(jié)點U 是黑色或缺少，新節(jié)點N 是其父節(jié)點的左子節(jié)點，而父節(jié)點P又是其父節(jié)點G的左子節(jié)點。在這種情形下，我們進行針對祖父節(jié)點G 的一次右旋轉(zhuǎn); 在旋轉(zhuǎn)產(chǎn)生的樹中，以前的父節(jié)點P現(xiàn)在是新節(jié)點N和以前的祖父節(jié)點G 的父節(jié)點。我們知道以前的祖父節(jié)點G是黑色，否則父節(jié)點P就不可能是紅色 (如果 P 和 G 都是紅色就違反了性質(zhì)4，所以 G 必須是黑色)。我們切換以前的父節(jié)點P和祖父節(jié)點G的顏色，結(jié)果的樹滿足性質(zhì)4^[3]。性質(zhì)5^[4]也仍然保持滿足，因為通過這三個節(jié)點中任何一個的所有路徑以前都通過祖父節(jié)點G ，現(xiàn)在它們都通過以前的父節(jié)點P。在各自的情形下，這都是三個節(jié)點中唯一的黑色節(jié)點。

 void insert_case5(node n) {
     n->parent->color = BLACK;
     grandparent(n)->color = RED;
     if (n == n->parent->left && n->parent == grandparent(n)->left) {
         rotate_right(grandparent(n));
     } else {
         /* Here, n == n->parent->right && n->parent == grandparent(n)->right */
         rotate_left(grandparent(n));
     }
 }

注意插入實際上是原地算法，因為上述所有調(diào)用都使用了尾部遞歸。

[編輯]刪除

如果需要刪除的節(jié)點有兩個兒子，那么問題可以被轉(zhuǎn)化成刪除另一個只有一個兒子的節(jié)點的問題（為了表述方便，這里所指的兒子，為非葉子節(jié)點的兒子）。對于二叉查找樹，在刪除帶有兩個非葉子兒子的節(jié)點的時候，我們找到要么在它的左子樹中的最大元素、要么在它的右子樹中的最小元素，并把它的值轉(zhuǎn)移到要刪除的節(jié)點中(如在這里所展示的那樣)。我們接著刪除我們從中復(fù)制出值的那個節(jié)點，它必定有少于兩個非葉子的兒子。因為只是復(fù)制了一個值而不違反任何屬性，這就把問題簡化為如何刪除最多有一個兒子的節(jié)點的問題。它不關(guān)心這個節(jié)點是最初要刪除的節(jié)點還是我們從中復(fù)制出值的那個節(jié)點。

在本文余下的部分中，我們只需要討論刪除只有一個兒子的節(jié)點(如果它兩個兒子都為空，即均為葉子，我們?nèi)我鈱⑵渲幸粋€看作它的兒子)。如果我們刪除一個紅色節(jié)點（此時該節(jié)點的兒子將都為葉子節(jié)點），它的父親和兒子一定是黑色的。所以我們可以簡單的用它的黑色兒子替換它，并不會破壞屬性3和4。通過被刪除節(jié)點的所有路徑只是少了一個紅色節(jié)點，這樣可以繼續(xù)保證屬性5。另一種簡單情況是在被刪除節(jié)點是黑色而它的兒子是紅色的時候。如果只是去除這個黑色節(jié)點，用它的紅色兒子頂替上來的話，會破壞屬性5，但是如果我們重繪它的兒子為黑色，則曾經(jīng)通過它的所有路徑將通過它的黑色兒子，這樣可以繼續(xù)保持屬性5。

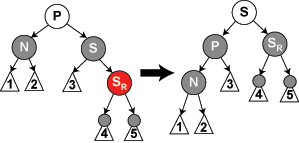
需要進一步討論的是在要刪除的節(jié)點和它的兒子二者都是黑色的時候，這是一種復(fù)雜的情況。我們首先把要刪除的節(jié)點替換為它的兒子。出于方便，稱呼這個兒子為N，稱呼它的兄弟(它父親的另一個兒子)為S。在下面的示意圖中，我們還是使用P稱呼N的父親，S_L稱呼S的左兒子，S_R稱呼S的右兒子。我們將使用下述函數(shù)找到兄弟節(jié)點:

struct node *
sibling(struct node *n)
{
        if (n == n->parent->left)
                return n->parent->right;
        else
                return n->parent->left;
}

我們可以使用下列代碼進行上述的概要步驟，這里的函數(shù) replace_node 替換 child 到 n 在樹中的位置。出于方便，在本章節(jié)中的代碼將假定空葉子被用不是 NULL 的實際節(jié)點對象來表示(在插入章節(jié)中的代碼可以同任何一種表示一起工作)。

void
delete_one_child(struct node *n)
{
        /*
         * Precondition: n has at most one non-null child.
         */
        struct node *child = is_leaf(n->right) ? n->left : n->right;
 
        replace_node(n, child);
        if (n->color == BLACK) {
                if (child->color == RED)
                        child->color = BLACK;
                else
                        delete_case1(child);
        }
        free(n);
}

如果 N 和它初始的父親是黑色，則刪除它的父親導(dǎo)致通過 N 的路徑都比不通過它的路徑少了一個黑色節(jié)點。因為這違反了屬性 4，樹需要被重新平衡。有幾種情況需要考慮:

情況 1: N 是新的根。在這種情況下，我們就做完了。我們從所有路徑去除了一個黑色節(jié)點，而新根是黑色的，所以屬性都保持著。

void
delete_case1(struct node *n)
{
        if (n->parent != NULL)
                delete_case2(n);
}

注意: 在情況2、5和6下，我們假定 N 是它父親的左兒子。如果它是右兒子，則在這些情況下的左和右應(yīng)當(dāng)對調(diào)。

情況 2: S 是紅色。在這種情況下我們在N的父親上做左旋轉(zhuǎn)，把紅色兄弟轉(zhuǎn)換成N的祖父。我們接著對調(diào) N 的父親和祖父的顏色。盡管所有的路徑仍然有相同數(shù)目的黑色節(jié)點，現(xiàn)在 N 有了一個黑色的兄弟和一個紅色的父親，所以我們可以接下去按 4、5或6情況來處理。(它的新兄弟是黑色因為它是紅色S的一個兒子。)

void
delete_case2(struct node *n)
{
        struct node *s = sibling(n);
 
        if (s->color == RED) {
                n->parent->color = RED;
                s->color = BLACK;
                if (n == n->parent->left)
                        rotate_left(n->parent);
                else
                        rotate_right(n->parent);
        } 
        delete_case3(n);
}

情況 3: N 的父親、S 和 S 的兒子都是黑色的。在這種情況下，我們簡單的重繪 S 為紅色。結(jié)果是通過S的所有路徑，它們就是以前不通過 N 的那些路徑，都少了一個黑色節(jié)點。因為刪除 N 的初始的父親使通過 N 的所有路徑少了一個黑色節(jié)點，這使事情都平衡了起來。但是，通過 P 的所有路徑現(xiàn)在比不通過 P 的路徑少了一個黑色節(jié)點，所以仍然違反屬性4。要修正這個問題，我們要從情況 1 開始，在 P 上做重新平衡處理。

void
delete_case3(struct node *n)
{
        struct node *s = sibling(n);
 
        if ((n->parent->color == BLACK) &&
            (s->color == BLACK) &&
            (s->left->color == BLACK) &&
            (s->right->color == BLACK)) {
                s->color = RED;
                delete_case1(n->parent);
        } else
                delete_case4(n);
}

情況 4: S 和 S 的兒子都是黑色，但是 N 的父親是紅色。在這種情況下，我們簡單的交換 N 的兄弟和父親的顏色。這不影響不通過 N 的路徑的黑色節(jié)點的數(shù)目，但是它在通過 N 的路徑上對黑色節(jié)點數(shù)目增加了一，添補了在這些路徑上刪除的黑色節(jié)點。

void
delete_case4(struct node *n)
{
        struct node *s = sibling(n);
 
        if ((n->parent->color == RED) &&
            (s->color == BLACK) &&
            (s->left->color == BLACK) &&
            (s->right->color == BLACK)) {
                s->color = RED;
                n->parent->color = BLACK;
        } else
                delete_case5(n);
}

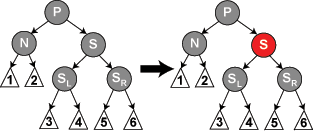
情況 5: S 是黑色，S 的左兒子是紅色，S 的右兒子是黑色，而 N 是它父親的左兒子。在這種情況下我們在 S 上做右旋轉(zhuǎn)，這樣 S 的左兒子成為 S 的父親和 N 的新兄弟。我們接著交換 S 和它的新父親的顏色。所有路徑仍有同樣數(shù)目的黑色節(jié)點，但是現(xiàn)在 N 有了一個右兒子是紅色的黑色兄弟，所以我們進入了情況 6。N 和它的父親都不受這個變換的影響。

void
delete_case5(struct node *n)
{
        struct node *s = sibling(n);
 
        if  (s->color == BLACK) /* this if statement is trivial, 
due to Case 2 (even though Case two changed the sibling to a sibling's child, 
the sibling's child can't be red, since no red parent can have a red child). */
// the following statements just force the red to be on the left of the left of the parent, 
// or right of the right, so case six will rotate correctly.
                if ((n == n->parent->left) &&
                    (s->right->color == BLACK) &&
                    (s->left->color == RED)) { // this last test is trivial too due to cases 2-4.
                        s->color = RED;
                        s->left->color = BLACK;
                        rotate_right(s);
                } else if ((n == n->parent->right) &&
                           (s->left->color == BLACK) &&
                           (s->right->color == RED)) {// this last test is trivial too due to cases 2-4.
                        s->color = RED;
                        s->right->color = BLACK;
                        rotate_left(s);
                }
        }
        delete_case6(n);
}

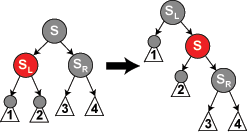
情況 6: S 是黑色，S 的右兒子是紅色，而 N 是它父親的左兒子。在這種情況下我們在 N 的父親上做左旋轉(zhuǎn)，這樣 S 成為 N 的父親和 S 的右兒子的父親。我們接著交換 N 的父親和 S 的顏色，并使 S 的右兒子為黑色。子樹在它的根上的仍是同樣的顏色，所以屬性 3 沒有被違反。但是，N 現(xiàn)在增加了一個黑色祖先: 要么 N 的父親變成黑色，要么它是黑色而 S 被增加為一個黑色祖父。所以，通過 N 的路徑都增加了一個黑色節(jié)點。

此時，如果一個路徑不通過 N，則有兩種可能性:

它通過 N 的新兄弟。那么它以前和現(xiàn)在都必定通過 S 和 N 的父親，而它們只是交換了顏色。所以路徑保持了同樣數(shù)目的黑色節(jié)點。
它通過 N 的新叔父，S 的右兒子。那么它以前通過 S、S 的父親和 S 的右兒子，但是現(xiàn)在只通過 S，它被假定為它以前的父親的顏色，和 S 的右兒子，它被從紅色改變?yōu)楹谏：铣尚Ч沁@個路徑通過了同樣數(shù)目的黑色節(jié)點。

在任何情況下，在這些路徑上的黑色節(jié)點數(shù)目都沒有改變。所以我們恢復(fù)了屬性 4。在示意圖中的白色節(jié)點可以是紅色或黑色，但是在變換前后都必須指定相同的顏色。

void
delete_case6(struct node *n)
{
        struct node *s = sibling(n);
 
        s->color = n->parent->color;
        n->parent->color = BLACK;
 
        if (n == n->parent->left) {
                s->right->color = BLACK;
                rotate_left(n->parent);
        } else {
                s->left->color = BLACK;
                rotate_right(n->parent);
        }
}

同樣的，函數(shù)調(diào)用都使用了尾部遞歸，所以算法是就地的。此外，在旋轉(zhuǎn)之后不再做遞歸調(diào)用，所以進行了恒定數(shù)目(最多 3 次)的旋轉(zhuǎn)。

[編輯]漸進邊界的證明

包含n個內(nèi)部節(jié)點的紅黑樹的高度是 O(log(n))。

定義:

h(v) = 以節(jié)點v為根的子樹的高度。
bh(v) = 從v到子樹中任何葉子的黑色節(jié)點的數(shù)目(如果v是黑色則不計數(shù)它)(也叫做黑色高度)。

引理: 以節(jié)點v為根的子樹有至少 $2 b h (v) - 1$ 個內(nèi)部節(jié)點。

引理的證明(通過歸納高度):

基礎(chǔ): h(v) = 0

如果v的高度是零則它必定是 nil，因此 bh(v) = 0。所以:

$2 b h (v) - 1 = 2 0 - 1 = 1 - 1 = 0$

歸納假設(shè): h(v) = k 的v有 $2 b h (v) - 1 - 1$ 個內(nèi)部節(jié)點暗示了 h( $v'$ ) = k+1 的 $v'$ 有 $2 b h (v') - 1$ 個內(nèi)部節(jié)點。

因為 $v'$ 有 h( $v'$ ) > 0 所以它是個內(nèi)部節(jié)點。同樣的它有黑色高度要么是 bh( $v'$ ) 要么是 bh( $v'$ )-1 (依據(jù) $v'$ 是紅色還是黑色)的兩個兒子。通過歸納假設(shè)每個兒子都有至少 $2 b h (v') - 1 - 1$ 個內(nèi)部接點，所以 $v'$ 有:

$2 b h (v') - 1 - 1 + 2 b h (v') - 1 - 1 + 1 = 2 b h (v') - 1$

個內(nèi)部節(jié)點。

使用這個引理我們現(xiàn)在可以展示出樹的高度是對數(shù)性的。因為在從根到葉子的任何路徑上至少有一半的節(jié)點是黑色(根據(jù)紅黑樹屬性4)，根的黑色高度至少是h(root)/2。通過引理我們得到:

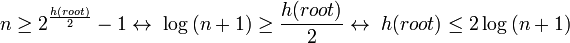
$n \geq 2^{{h(root) \over 2}} - 1 \leftrightarrow \; \log{(n+1)} \geq {h(root) \over 2} \leftrightarrow \; h(root) \leq 2\log{(n+1)}$

因此根的高度是O(log(n))。

[編輯]注釋

^ 性質(zhì)1. 節(jié)點是紅色或黑色。
^ 性質(zhì)3. 所有葉子都是黑色。
^ ^3.0 ^3.1 ^3.2 ^3.3 性質(zhì)4. 每個紅色節(jié)點的兩個子節(jié)點都是黑色。
^ ^4.0 ^4.1 ^4.2 ^4.3 ^4.4 ^4.5 性質(zhì)5. 從每個葉子到根的所有路徑都包含相同數(shù)目的黑色節(jié)點。
^ 性質(zhì)2. 根是黑色。

[編輯]引用

Mathworld: Red-Black Tree
San Diego State University: CS 660: Red-Black tree notes, by Roger Whitney
Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms. Massachusetts: The MIT Press, 2002. pp273-77. ISBN 0-07-013151-1

[編輯]外部鏈接

相關(guān)的維基共享資源：

紅黑樹

An applet + quick explanation
Red/Black Tree Demonstration
An example (animated GIF, 200KB)
An example (static picture)
Another explanation (pictures, source code, and Java interactive animation)
Red-Black Tree Demonstration by David M. Howard
RBT: A SmallEiffel Red-Black Tree Library
libredblack: A C Red-Black Tree Library
Red-Black Tree C++ Code
Red-Black Trees by Thomas Niemann
紅黑樹的介紹和實現(xiàn)

posted on 2011-05-20 17:19 老馬驛站閱讀(430) 評論(0) 編輯收藏引用所屬分類: c++ 、algorithm

目錄

[編輯]用途和好處

[編輯]性質(zhì)

[編輯]操作

[編輯]插入

[編輯]刪除

[編輯]漸進邊界的證明

[編輯]參見

[編輯]注釋

[編輯]引用

[編輯]外部鏈接

常用鏈接

留言簿(3)

隨筆分類

隨筆檔案

收藏夾

搜索

最新評論

閱讀排行榜

評論排行榜