題目大意是求解快排最壞情況下的交換次數(shù)，我們知道，快速排序在最壞情況下會(huì)退化為冒泡排序，因此快排最壞情況下的交換次數(shù)也就是冒泡排序?qū)?yīng)的交換次數(shù)。很容易想到這一題用冒泡排序，并記錄交換次數(shù)就行了。
這樣做看似可行，其實(shí)是行不通的，數(shù)據(jù)量是500000，由于冒泡排序的時(shí)間復(fù)雜度是O(N^2)，所以問題的規(guī)模就是500000^2=2.5 * E11，一般我們認(rèn)為計(jì)算機(jī)每秒的計(jì)算量是E9，因此用冒泡排序是行不通的。
聯(lián)想有關(guān)排序的算法，我們希望這一題的時(shí)間復(fù)雜度能夠降為O(NlogN)，快排、堆排序、合并排序滿足這樣的要求，可是前兩種排序方式的交換方式毫無規(guī)律可循，只剩下歸并排序。
我們來看歸并排序，它的核心是歸并（由Merge()函數(shù)實(shí)現(xiàn)），就是將兩個(gè)有序序列合并為一個(gè)有序序列。由冒泡排序我們知道，交換的總次數(shù)就是初始序列中每個(gè)元素交換次數(shù)的總和，每個(gè)元素的交換次數(shù)等于該元素后面比自己小的元素的個(gè)數(shù)（因?yàn)樽罱K比自己小的元素都在自己前面）。
下圖是一次Merge()過程：

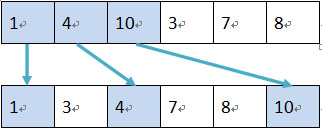
可以看出，元素“1”沒有移動(dòng)，元素“4”向后移動(dòng)了1位，元素“10”向后移動(dòng)了3位，所以本次合并共移動(dòng)了4次。統(tǒng)計(jì)合并排序過程中所有的移動(dòng)次數(shù)即可。
本題代碼如下

#include<stdio.h>
#include<stdlib.h>
#define LEN 500010
long long count;
void Copy(int *a, int *b, int f, int r)
{
    for(int i = 0; i <= r - f; i++)
        a[i + f] = b[i];
}
void Merge(int *a, int f, int m, int r)
{
    int *b = (int *)malloc(sizeof(int) * ( r - f + 1));
    int i = f;
    int j = m + 1;
    int k = 0;
    while(i <= m && j <= r)
    {
        if(a[i] > a[j])
            b[k++] = a[j++];
        else
        {
            b[k++] = a[i++];
            if(k + f > i)
                count += k + f - i;
        }
    }
    while(i <= m)
    {
        b[k++] = a[i++];
        if(k + f > i)
            count += k + f - i;
    }
    while(j <= r)
        b[k++] = a[j++];
    Copy(a, b, f, r);
    free(b);
}

void MergeSort(int *a, int f, int r)
{
    if(f < r)
    {
        int i = (r + f) / 2;
        MergeSort(a, f, i);//ÅÅÐò×ó°ë²¿·Ö
        MergeSort(a, i + 1, r);//ÅÅÐòÓҰ벿·Ö
        Merge(a, f, i, r);//ºÏ²¢   
    }
}
int main()
{
    int i, j;
    int N;
    int a[LEN];
    scanf("%d", &N);
    while(N != 0)
    {
        for(i = 1; i <= N; i++)
            scanf("%d", &a[i]);
        count = 0;
        MergeSort(a, 1, N);
        printf("%lld\n", count);
        scanf("%d", &N);
    }
    //system("pause");
    
}

有關(guān)合并排序請(qǐng)參閱：
http://m.shnenglu.com/hoolee/archive/2012/07/18/184029.html 合并排序是利用了分治思想的排序方式，具有O(NlogN)的時(shí)間復(fù)雜度，與快速排序、堆排序相比，它需要N的輔助空間。它的核心部分是將兩個(gè)有序序列合并（由Merge()函數(shù)實(shí)現(xiàn)）。
合并排序的基本思想是：單個(gè)元素是有序的，兩個(gè)較小的有序序列可被合并為一個(gè)較大的有序序列。
算法描述如下： 直接插入排序，時(shí)間復(fù)雜度O(N^2)，基本操作是將一個(gè)元素插入到有序序列中。當(dāng)待排序元素個(gè)數(shù)為n時(shí)，因?yàn)榈谝粋€(gè)元素是有序的，因此只需經(jīng)過n - 1次插入，就能完成排序。
單次插入的過程為：
1.找到要插入元素在已排序部分中的位置j。
2.將有序序列中j后面的所有元素向后移動(dòng)一位，為待插入元素空出位置。
3.將待排序元素插入j位置，保持序列有序。
算法描述為：


     摘要: 快速排序是運(yùn)用了分治思想的排序方式，具有O(NlogN)的平均時(shí)間復(fù)雜度，極端情況下時(shí)間復(fù)雜度為O(N^2)，跟冒泡排序一樣，但是快排的實(shí)際效率遠(yuǎn)比最壞情況好很多。它的關(guān)鍵部分是一輪選擇（由Partition()函數(shù)完成）……所謂線性時(shí)間就是在平均O(N)的時(shí)間內(nèi)找出無序序列中第k大的元素。它是以Partition()函數(shù)的劃分為依據(jù)的……  閱讀全文      摘要: 奇數(shù)個(gè)數(shù)尋找中位數(shù)，有O(N)復(fù)雜度的算法，這里采用的方式是先排序，然后找出中間那一個(gè)，等寫到快排時(shí)在寫線性時(shí)間的算法吧。以下采用的方式分別是冒泡排序和堆排序： Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlighter.com/--> 1#include<...  閱讀全文

冒泡排序是最基本的排序方式，很簡單，容易理解，但算法的時(shí)間復(fù)雜度為O(N^2)，適合于基數(shù)不大的排序。
下面的代碼中bsort函數(shù)完成冒泡排序，數(shù)組下標(biāo)從1開始。

 

     摘要: 堆排序是一種比較常用的排序方式，具有O(NlogN)的時(shí)間復(fù)雜度，它只需要一個(gè)記錄大小的空間，算法的核心是“篩選”。
堆的存儲(chǔ)方式是一維數(shù)組，因?yàn)樗且豢猛耆鏄洌⒆优c雙親下標(biāo)有簡單直接的計(jì)算方式……  閱讀全文      摘要: Java中的基本數(shù)據(jù)類型使用"=="可以判斷操作數(shù)是否相等，對(duì)于對(duì)象則判斷這兩個(gè)對(duì)象的內(nèi)存地址是否相同。Java虛擬機(jī)為了提高字符串應(yīng)用效率，提供了字符串池來保存字符串常量，str1創(chuàng)建字符串常量"abc"時(shí)，虛擬機(jī)會(huì)先檢測(cè)字符串池中是否包含該字符串……  閱讀全文      摘要: http://poj.org/problem?id=2251一道三維的迷宮題，要求求出最短路徑。廣度優(yōu)先搜索的框架是很清晰的，就是在code的時(shí)候一些細(xì)節(jié)注意不到，就只好調(diào)啊，調(diào)啊，就這樣兩個(gè)小時(shí)就過去了%>_<%說一下代碼思路吧：1.讀入數(shù)據(jù)2.預(yù)處理迷宮，主要是給迷宮周圍加一道墻，便于統(tǒng)一處理3.找到起點(diǎn)'S'，和終點(diǎn)'E'的坐標(biāo)分別記錄在p0、p1中4.從起點(diǎn)開始進(jìn)行廣搜，直到隊(duì)...  閱讀全文 與排列相比，組合是不區(qū)分元素順序的，為了消去相同元素不同順序的干擾項(xiàng)，在選取每一個(gè)組合項(xiàng)的元素時(shí)使該元素的位序大于已選好元素的位序即可。如果題目要求所有組合項(xiàng)按升序輸出，只需事先將所有元素排序即可。
http://acm.nyist.net/JudgeOnline/problem.php?pid=541
這是省賽的第二題。
題意：把一個(gè)整數(shù)拆分成若干份，每一份相加的和為這個(gè)數(shù)，求這些數(shù)最大的積。
如果能夠分析出應(yīng)把原數(shù)拆為3+3+3+3+3……，接下來需要的就是大數(shù)運(yùn)算了（悲劇的是我們當(dāng)時(shí)沒有分析出來):）。java中有BigInteger類來處理里大整數(shù)，比用C語言模擬大數(shù)運(yùn)算方便的多。
這是我的第一道java大數(shù)題，感覺寫的還有待改進(jìn)，用的不熟練。