十二����、二叉堆(Binary Heap)
經歷了上一篇實現AVL樹的繁瑣,這篇就顯得非常easy了�����。
首先說說數據結構概念——堆(Heap)��,其實也沒什么大不了����,簡單地說就是一種有序隊列而已����,普通的隊列是先入先出,而二叉堆是:最小先出。
這不是很簡單么�����?如果這個隊列是用數組實現的話那用打擂臺的方式從頭到尾找一遍�����,把最小的拿出來不就行了����?行啊�����,可是出隊的操作是很頻繁的�����,而每次都得打一遍擂臺,那就低效了,打擂臺的時間復雜度為Ο(n)����,那如何不用從頭到尾fetch一遍就出隊呢����?二叉堆能比較好地解決這個問題�����,不過之前先介紹一些概念。
完全樹(Complete Tree):從下圖中看出��,在第n層深度被填滿之前�����,不會開始填第n+1層深度�����,還有一定是從左往右填滿。
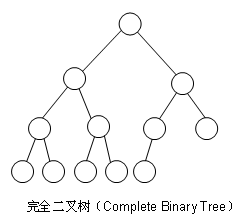
再來一棵完全三叉樹:

這樣有什么好處呢�����?好處就是能方便地把指針省略掉����,用一個簡單的數組來表示一棵樹,如圖:
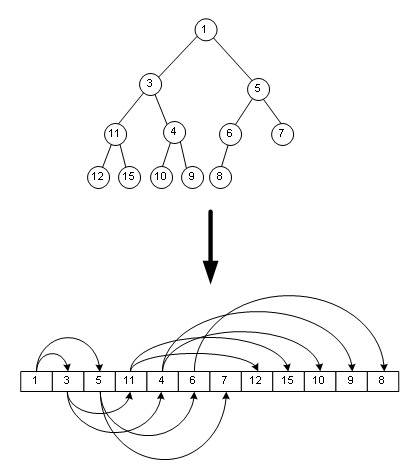
那么下面介紹二叉堆:二叉堆是一種完全二叉樹����,其任意子樹的左右節點(如果有的話)的鍵值一定比根節點大��,上圖其實就是一個二叉堆。
你一定發覺了�����,最小的一個元素就是數組第一個元素����,那么二叉堆這種有序隊列如何入隊呢�����?看圖:
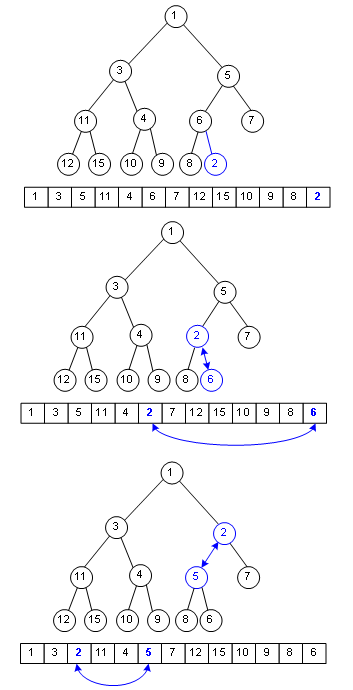
假設要在這個二叉堆里入隊一個單元�����,鍵值為2��,那只需在數組末尾加入這個元素,然后盡可能把這個元素往上挪����,直到挪不動��,經過了這種復雜度為Ο(logn)的操作,二叉堆還是二叉堆����。
那如何出隊呢�����?也不難,看圖:
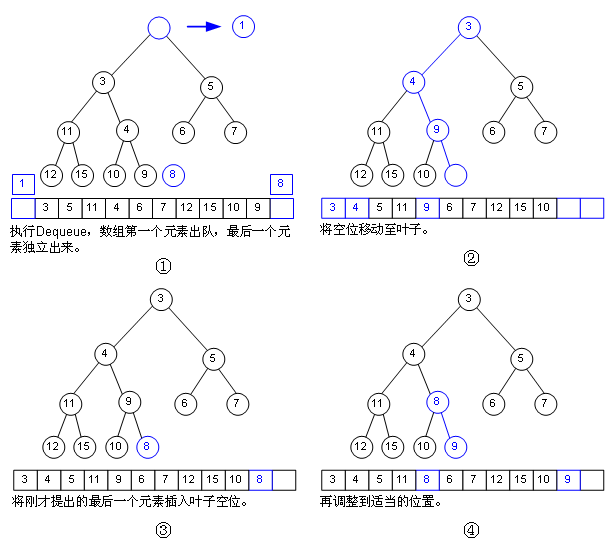
出隊一定是出數組的第一個元素��,這么來第一個元素以前的位置就成了空位����,我們需要把這個空位挪至葉子節點,然后把數組最后一個元素插入這個空位��,把這個“空位”盡量往上挪����。這種操作的復雜度也是Ο(logn)����,比Ο(n)強多了吧?
嘗試自己寫寫代碼看�����,當然了�����,我也寫(這個得動動手啦��,比AVL容易多了):
#include "stdio.h"
#define SWAP_TWO_INT(a, b) \
a^=b; b^=a; a^=b;
class CBinaryHeap
{
public:
CBinaryHeap(int iSize = 100);
~CBinaryHeap();
//Return 0 means failed.
int Enqueue(int iVal);
int Dequeue(int &iVal);
int GetMin(int &iVal);
#ifdef _DEBUG
void PrintQueue();
#endif
protected:
int *m_pData;
int m_iSize;
int m_iAmount;
};
CBinaryHeap::CBinaryHeap(int iSize)
{
m_pData = new int[iSize];
m_iSize = iSize;
m_iAmount = 0;
}
CBinaryHeap::~CBinaryHeap()
{
delete[] m_pData;
}
#ifdef _DEBUG
int CBinaryHeap::Enqueue(int iVal)
{
if(m_iAmount==m_iSize)
return 0;
//Put this value to the end of the array.
m_pData[m_iAmount] = iVal;
++m_iAmount;
int iIndex = m_iAmount - 1;
while(m_pData[iIndex] < m_pData[(iIndex-1)/2])
{
//Swap the two value
SWAP_TWO_INT(m_pData[iIndex], m_pData[(iIndex-1)/2])
iIndex = (iIndex-1)/2;
}
return 1;
}
#endif
int CBinaryHeap::Dequeue(int &iVal)
{
if(m_iAmount==0)
return 0;
iVal = m_pData[0];
int iIndex = 0;
while (iIndex*2<m_iAmount)
{
int iLeft = (iIndex*2+1 < m_iAmount)?(iIndex*2+1):0;
int iRight = (iIndex*2+2 < m_iAmount)?(iIndex*2+2):0;
if(iLeft && iRight) // Both left and right exists.
{
if(m_pData[iLeft]<m_pData[iRight])
{
SWAP_TWO_INT(m_pData[iIndex], m_pData[iLeft])
iIndex = iLeft;
}
else
{
SWAP_TWO_INT(m_pData[iIndex], m_pData[iRight])
iIndex = iRight;
}
}
else if(iLeft) //The iRight must be 0
{
SWAP_TWO_INT(m_pData[iIndex], m_pData[iLeft])
iIndex = iLeft;
break;
}
else
{
break;
}
}
//Move the last element to the blank position.
//Of course, if it is the blank one, forget it.
if(iIndex!=m_iAmount-1)
{
m_pData[iIndex] = m_pData[m_iAmount-1];
//Try to move this element to the top as high as possible.
while(m_pData[iIndex] < m_pData[(iIndex-1)/2])
{
//Swap the two value
SWAP_TWO_INT(m_pData[iIndex], m_pData[(iIndex-1)/2])
iIndex = (iIndex-1)/2;
}
}
--m_iAmount;
return 1;
}
int CBinaryHeap::GetMin(int &iVal)
{
if(m_iAmount==0)
return 0;
iVal = m_pData[0];
return 1;
}
void CBinaryHeap::PrintQueue()
{
int i;
for(i=0; i<m_iAmount; i++)
{
printf("%d ", m_pData[i]);
}
printf("\n");
}
int main(int argc, char* argv[])
{
CBinaryHeap bh;
bh.Enqueue(4);
bh.Enqueue(1);
bh.Enqueue(3);
bh.Enqueue(2);
bh.Enqueue(6);
bh.Enqueue(5);
#ifdef _DEBUG
bh.PrintQueue();
#endif
int iVal;
bh.Dequeue(iVal);
bh.Dequeue(iVal);
#ifdef _DEBUG
bh.PrintQueue();
#endif
return 0;
}