http://blog.csdn.net/raodotcong/article/details/6429991
最近看了篇Paper,里面出現(xiàn)了一個(gè)超圖(Hypergraph)的概念�����,論文里的解釋不是很清楚����,所以不是很懂,這里研究下子。
超圖(Hypergraph)是什么
簡(jiǎn)單的來(lái)說(shuō),對(duì)于我們熟悉的圖而言�����,它的一個(gè)邊(edge)只能和兩個(gè)頂點(diǎn)連接��;而對(duì)于超圖來(lái)講����,人們定義它的邊(這里叫超邊,hyperedge)可以和任意個(gè)數(shù)的頂點(diǎn)連接����。一個(gè)圖和超圖的示意圖如下所示:
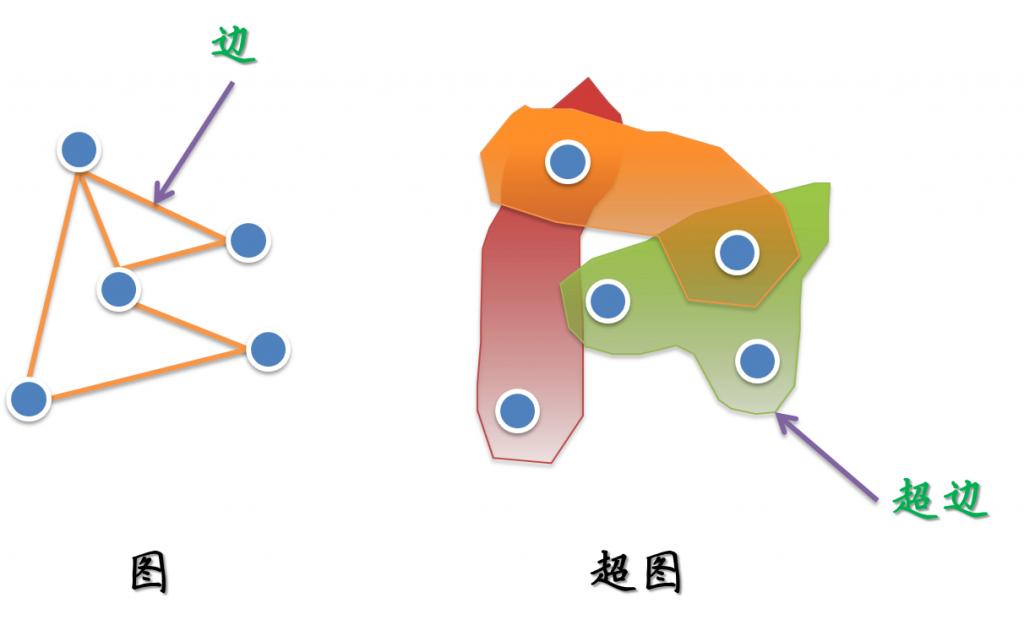
而對(duì)于超圖的一個(gè)嚴(yán)格的數(shù)學(xué)定義����,維基百科上是這樣寫(xiě)的:
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = (X,E) where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links.
k-均勻超圖(k-uniform hypergraph)
對(duì)于超圖而言��,還有一個(gè)k-均勻超圖的概念(k-uniform hypergraph)。它指超圖的每個(gè)邊連接的頂點(diǎn)個(gè)數(shù)都是相同的��,即為個(gè)數(shù)k。所以2-均勻超圖就是我們傳統(tǒng)意義上的圖�����,3-均勻超圖就是一個(gè)三元組的集合,以此類推����。
While graph edges are pairs of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often useful to study hypergraphs where all hyperedges have the same cardinality: a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, it is a collection of sets of size k.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of triples, and so on.