?
一、用向量空間解方程組
?
1�、向量和向量空間
?
(1) 二維空間R2中的向量用兩個沿列向的元素表示。
?
 ?
?
?
向量u,v在二維空間的表示:
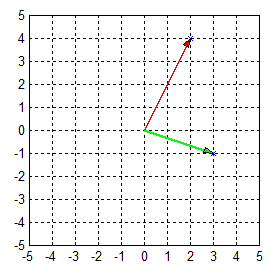
?
(2)??二維向量張成的空間
平面上的任何一點[w1;w2]是不是一定能用u和v的線性組合來實現�?即是不是一定能找到一組常數[c1,c2],使得
?

?
? c1,c2取所有可能的值��,得到的w的集合就是u和v張成的子空間,在所給的u和v下�,它是一個平面��。
? 若u和v兩個向量的各元素成簡單的比例關系,合成的向量只能在一根直線上����,不可能張成整個二維平面����。這種情況下��,稱這兩個向量u和v是線性相關的����。?
?
(3)??三維空間中的向量
?
若v1,v2和v3都是三維空間的列向量�?�?梢杂每臻g坐標中的三個點,或從坐標原點引向這三點的箭頭來表示����。用矩陣代數表示如下:
?
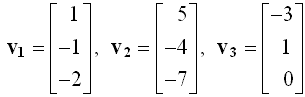
?
如果三個基本向量之間線性無關��,那么它們的線性組合可以覆蓋(張成)整個三維空間。如果三個向量共面,即相關,就不能張成三維空間��。判斷三個向量的線性相關性����,可用行列式。
?
(4) 三維空間向量的相關性
?
det(A)=0? 相關
det(A)≠0? 不相關
行列式的幾何意義:在二維是兩個向量組成的平行四邊形面積,在三維是三個向量組成的平行六面體的體積。
?
(5) n維向量的相關性
在進入三維以上的空間時����,已經沒有可與面積、體積直接相當的概念可用了����,所以采用了秩的概念��。如果A的行列式為零,也就是它的秩r小于n時����,說明這n個向量是線性相關的�。
秩的概念也概括了面積存在(r=2)和體積存在(r=3)的意義��,因此�,它是更高度的抽象����。
?
(6) 向量空間和基向量
? 若r個向量是線性無關的,則它們的線性組合的全體V就構成了r維空間Rr��。如果它不是空集����,則V稱為向量空間。生成V的r個線性無關的向量v稱為基向量或基(Basis)��。
? 當r=n時�,給定的n個向量就是一組基。如果r<n����,那就要在n個向量中選出r個線性無關的向量�。用秩的概念還無法判定哪些向量是線性無關的����,這時又要藉助于把矩陣簡化為階梯形式的方法。
?
例1:求四個五維向量的子空間
這四個向量組成的矩陣如下��,對它進行行階梯簡化:
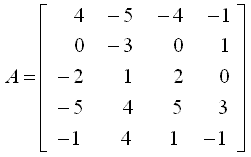
程序為:
>>?A=[4,-5,-4,-1;0,-3,0,1;-2,1,2,0;-5,4,5,3;-1,4,1,-1]
[U0,ip]=rref(A)
A?=
?????4????-5????-4????-1
?????0????-3?????0?????1
????-2?????1?????2?????0
????-5?????4?????5?????3
????-1?????4?????1????-1
U0?=
?????1?????0????-1?????0
?????0?????1?????0?????0
?????0?????0?????0?????1
?????0?????0?????0?????0
?????0?????0?????0?????0
ip?=
?????1?????2?????4
>>?
?
得到 ip=1,2,4��,其三個樞軸列對應的就是三個線性無關的列向量。
?
例2:w是否在v1,v2,v3的空間內
設
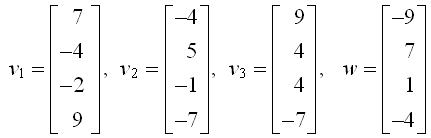
?
w是否能由v1,v2,v3的線性組合構成的問題,取決于線性方程組 v.c=w 解的存在性。
程序為:
v1=[7;-4;-2;9];?
v2=[-4;5;-1;-7];?
v3=[9;4;4;-7];?
w=[-9;7;1;-4];?
v=[v1,v2,v3];
c=v\w?????
%?把基向量組成矩陣v求解
?
也可以按det(v)是否為零進行判別��。
?
(7) 向量的內積和正交性
兩個m維向量的內積可以寫成:
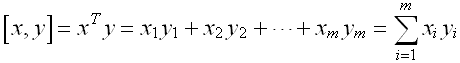
這是一個標量��。向量x與自己求內積
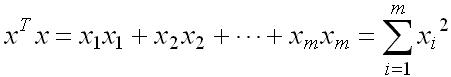
得到的是其各分量的平方和�,其平方根就等于向量的長度(或模��、或范數norm)�。
?
(8) 內積的幾何意義
在平面情況�,兩向量的內積除以它們的長度是它們夾角的余弦:
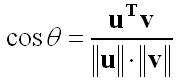
?
例3:基向量長度規一化和夾角
求以上例2中的單位基向量v01,v02,v03,并分別求它們之間的夾角。
?
程序為:
v10=v1/norm(v1)
v20=v2/norm(v2)?
v30=v3/norm(v1)
theta12=acos((v1'*v2)/(norm(v1)*norm(v2)))
theta13=acos((v1'*v3)/(norm(v1)*norm(v3)))
theta23=acos((v3'*v2)/(norm(v3)*norm(v2)))
?
(9)?正交基向量的生成
兩向量x��,y正交的條件是它們的內積為零�。
給出向量求正交基常用施密特算法,ATLAST手冊中給出了相應的程序gschmidt。調用時鍵入[Q,R]=gschmidt(v),Q就是單位正交基向量e。
MATLAB中不用施密特算法,而用更好的算法編成了正交分解子程序qr.m,它將v分解為Q和R兩個矩陣的乘積。調用方法為:[Q,R]=qr(v) ,Q就是m×m單位正交矩陣����。
?
基向量正交化的schmidt公式:

得到qi(i?1,2,…,k)后�,再把它們除以norm(qi)�,就可歸一化為單位向量ek。
?
基向量正交化的gschmidt子程序:
function?[Q,R]=gschmidt(V)
[m,n]=size(V);?R=zeros(n);
R(1,1)=norm(V(:,1));
Q(:,1)=V(:,1)/R(1,1);
for?k=2:n
????R(1:k-1,k)=Q(:,1:k-1)'*V(:,k);
????Q(:,k)=V(:,k)-Q(:,1:k-1)*R(1:k-1,k);
????R(k,k)=norm(Q(:,k));
????Q(:,k)=Q(:,k)/R(k,k);
end
?
例4:對于例2的數據,求其規范化正交基向量e1,e2,…,en��。
>>?V=[7,-4,9;-4,5,4;-2,-1,4;9,-7,-7]
[Q,R]=qr(V)?%?或?[Q,R]=gschmidt(V)?
e=Q(:,[1:3])
V?=
?????7????-4?????9
????-4?????5?????4
????-2????-1?????4
?????9????-7????-7
Q?=
???-0.5715???-0.3164???-0.7473???-0.1217
????0.3266???-0.6096???-0.1080????0.7142
????0.1633????0.7144???-0.5022????0.4591
???-0.7348????0.1339????0.4216????0.5141
R?=
??-12.2474????8.8998????1.9596
?????????0???-3.4341???-3.3662
?????????0?????????0??-12.1173
?????????0?????????0?????????0
e?=
???-0.5715???-0.3164???-0.7473
????0.3266???-0.6096???-0.1080
????0.1633????0.7144???-0.5022
???-0.7348????0.1339????0.4216
>>?
?
得到e=[e1 e2 e3]
?
?
?
二��、線性變換及特征
?
1�、平面上線性變換的幾何意義
?
例1? 設x為二維平面上第一象限中的一個單位方塊����,其四個頂點的數據可寫成:
?
x?=
?????0?????1?????1?????0
?????0?????0?????1?????1
?
把不同的A矩陣作用于此組數據,可以得到多種多樣的結果yi=Ai*x。

可以看出,矩陣A1使原圖對縱軸生成鏡像��,矩陣A2使原圖在橫軸方向膨脹,矩陣A3使原圖在縱軸方向壓縮�,矩陣A4使原圖向右方剪切變形��,矩陣A5使原圖沿反時針方向旋轉t?pi/6。分別計算出這五個矩陣的行列式和特征值: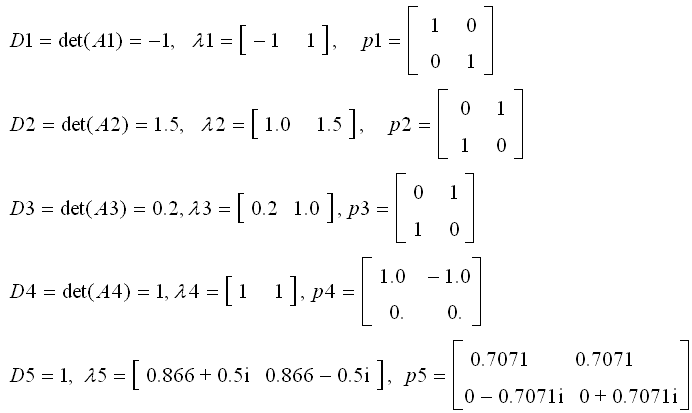 ?
?
對二維空間(平面)��,行列式的幾何意義實際上是兩個向量所構成的平行四邊形的面積�。一個變換所造成的圖形的面積變化,取決于該變換的行列式�。A1��,A4和A5的行列式絕對值都是1,所以它們不會使變換后圖形的面積發生改變��。而A2和A3的行列式分別為1.5和0.2����。
?
2����、二維矩陣特征值的幾何意義
(1) 二維矩陣的特征值表示該變換在原圖形的特征向量的方向上的放大量。例如矩陣A1在第一特征向量
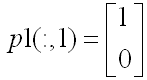
的方向的特征值為λ1(1) = -1,即橫軸正方向的增益為-1��,其結果是把原圖中橫軸正方向的部分變換到新圖的負方向去了�;A1在第二特征向量
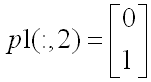
的方向的特征值為λ1(2)=1,即縱軸正方向的增益為1,因而保持了新圖和原圖在縱軸方向尺度不變。
?
例2:斜體字的生成
數據矩陣
x?=
?????????0????0.5000????0.5000????6.0000????6.0000????5.5000????5.5000?????????0
?????????0?????????0????6.4200?????????0????8.0000????8.0000????1.5800????8.0000
?
表示英文大寫空心字母N的各個節點
(1)用plot語句在子圖1中畫出其形狀�;
(2)取
A?=
????1????0.25
????0????1
?
作為變換矩陣對x進行變換�,并在子圖2中畫出其圖形��;
畫圖的要點是要在給定的數據右方����,補上第一點的坐標�,使畫出的圖形封閉。
?
程序為:
x0?=?[0,0.5,0.5,6,6,5.5,5.5,0;0,0,6.42,0,8,8,1.58,8]
x?=?[x0,x0(:,1)]?%?把首頂點坐標補到末頂點后
A?=?[1,0.25;0,1]
y?=?A*x
subplot(1,2,1),?plot(x(1,:),x(2,:))
subplot(1,2,2),?plot(y(1,:),y(2,:))
?
畫出的兩個圖形為:

(2) 平移運動不能用二維變換實現
剛體在平面上的運動要用兩個平移和一個轉動來描述,轉動可以從上面的線性變換A5得到��,但平移y=x+c卻不是一個線性變換����。因為:
(1)設ya = xa+c;yb = xb+c;則它們的和為
??y = ya+yb = xa+xb+2c ≠ x+c,
可見����,它對加法不封閉����;
(2)設ya = xa+c�;將它乘以常數k,
??y = kya = k(xa+c) = kxa+kc ≠ kxa+c = x+c,
可見��,它對乘法也不封閉����;就是說�,這不符合線性變換的規則,x和y 不屬于同一個向量空間�,無法用矩陣乘法來實現平移變換y = x+c��。
?
(3) 平面運動模型的齊次坐標系
把平面問題映射到高維的空間來建立方程,有可能把x和y由擴展了的向量空間來覆蓋�。把原來通過原點的平面沿垂直方向提高一個單位�,與原平面保持平行�,于是原來的x就用三維向量來表示為:

這樣的坐標系稱為齊次坐標系。
此時可以把平移矩陣寫成:
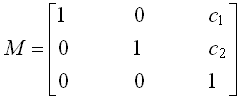
因而平移運動y就可用x經線性變換實現了�。
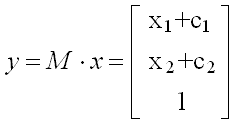
這個方法在研究剛體平面運動時非常有用��。
對象若同時有旋轉和平移,則可以分別列出旋轉矩陣和平移矩陣�。不過此時的旋轉矩陣也要改為3×3維����,這可以把上述A5中增加第三行和第三列�,置A(3,3)=1,其余新增元素為零��。
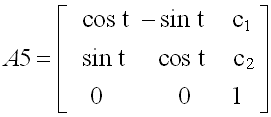
這就是既包括平移�,又包括轉動的平面齊次坐標系內的變換矩陣。
?
(4) 空間線性變換的幾何意義
三維空間線性變換最直接的幾何意義和應用價值可以從飛行器的三維轉動坐標中得到解釋����。飛行器在空中可以圍繞三個軸旋轉�。假如它在向北飛行����,機頭正對北方,則它圍繞鉛垂軸的旋轉角稱為偏航角(Yaw)�,它描述了飛機左右的偏轉��,用u表示;圍繞翼展軸的旋轉角稱為傾斜角(Pitch)����,它描述了飛機俯仰姿態����,用v表示����;圍繞機身軸的旋轉角稱為滾動角(Roll),用w表示��;u,v和w三個變量統稱為歐拉角��,它們完全地描述了飛機的姿態����。
?
例3:程序的實現方法
把飛行器的三維圖像用N個頂點描述����,寫成一個3×N的數據矩陣G。用plot3命令時按頂點連線能繪制出飛行器的外觀�。例如以下程序即可畫出一個最簡單的飛行器立體圖����。
Gw=[-4,-3,0;4,-3,0;0,7,0;-4,-3,0]';?%?主翼的頂點坐標
Gt=[0,-3,0;0,-3,3;0,2,0;0,-3,0]';?%?尾翼的頂點坐標
G=[Gw,Gt]?%?整個飛行器外形的數據集
plot3(Gw(1,:),Gw(2,:),Gw(3,:),'r'),?hold?on
plot3(Gt(1,:),Gt(2,:),Gt(3,:),'g'),?axis?equal
?
圍繞各個軸的旋轉變換矩陣:
飛行器圍繞各個軸的旋轉的結果��,表現為各個頂點坐標發生變化�,也就是G的變化��。只要把三種姿態的變換矩陣Y,P和R乘以圖形數據矩陣G即可����。其中

?
綜合旋轉的變換矩陣:
單獨變化某個姿態角所生成的圖形由G1 = Y*G�,G2 = P*G,G3 = R*G算出��,如果同時變化三個姿態角��,則最后的圖像數據成為Gf = Y*P*R*G = Q*G��。這里假定轉動的次序為:先滾動R��,再傾斜P����,最后偏航Y��,由于矩陣乘法不服從交換律����,轉動次序不同時結果也不同����。
用MATLAB實現的程序如下:
>>?syms?u,w,v
Y=[cos(u),sin(u),0;-sin(u),cos(u),0;0,0,1]
R=[1,0,0;0,cos(w),-sin(w);0,sin(w),cos(w)]
P=[cos(v),0,-sin(v);0,1,0;sin(v),0,cos(v)]
Q=Y*P*R?
?
w?=
w
?
?
v?=
v
?
?
Y?=
?
[??cos(u),??sin(u),???????0]
[?-sin(u),??cos(u),???????0]
[???????0,???????0,???????1]
?
R?=
?
[???????1,???????0,???????0]
[???????0,??cos(w),?-sin(w)]
[???????0,??sin(w),??cos(w)]
?
P?=
?
[??cos(v),???????0,?-sin(v)]
[???????0,???????1,???????0]
[??sin(v),???????0,??cos(v)]
?
Q?=
?
[??cos(u)*cos(v),??sin(u)*cos(w)-cos(u)*sin(v)*sin(w),?-sin(u)*sin(w)-cos(u)*sin(v)*cos(w)]
[?-sin(u)*cos(v),??cos(u)*cos(w)+sin(u)*sin(v)*sin(w),?-cos(u)*sin(w)+sin(u)*sin(v)*cos(w)]
[?????????sin(v),???????????????????????cos(v)*sin(w),???????????????????????cos(v)*cos(w)]
>>?
?