
這也算一個數(shù)學(xué)類的雜題吧。題目本身比較有意思,解題的思路很需要猜想。題目的意思用+和-去替代式子(? 1 ? 2 ? ... ? n = k)中
的?號,對于指定的K,求最小的n。
For example: to obtain k = 12 , - 1 + 2 + 3 + 4 + 5 + 6 - 7 = 12 with n = 7。
這個題,我的思路大致如下。首先,K可能是正的也是負(fù)的,而且顯然負(fù)的情況,有相應(yīng)的正對應(yīng)情況。那么考慮所有k為正的情況。
由于k一定小于等于n*(n+1)/2的,所以可以先求出這樣的最小n。這個可以二分搜索,或者直接用解不等式方程(不過這種方法一直wa了)。
然后就剩下的是第二點(diǎn)了,假設(shè)a + b = n*(n+1)/2, a - b = k。可以得到
n*(n+1)/2 - k = 2 * b。意思是,必須滿足
n*(n+1)/2
和k的差為偶數(shù)。假如滿足了,這樣的n是不是一定OK了???
答案是肯定的,這一點(diǎn)就是需要猜想的地方了。因?yàn)椋屑?xì)觀察下,1到n的數(shù)字可以組合出任意的1到 n*(n+1)/4之間的數(shù)字,這個數(shù)字
即是b。至于證明,可以用數(shù)學(xué)歸納法從n==1開始證明了。。。至此已經(jīng)很簡單了。
由于求n存在2種不同的方法,而且我開始用解一元二次不等式的方法求的N,出現(xiàn)了浮點(diǎn)誤差,一直WA了。后面改成二分才過了。。。
代碼如下:
#include <stdio.h>
#include <math.h>
int GetN(int nK)
{
int nBeg = 1;
int nEnd = sqrt(nK * 2) + 2;
while (nBeg <= nEnd)
{
int nMid = (nBeg + nEnd) / 2;
int nTemp = (nMid * nMid + nMid) / 2;
if (nTemp >= nK)
{
nEnd = nMid - 1;
}
else
{
nBeg = nMid + 1;
}
}
return nEnd + 1;
}
int main()
{
int nK;
int nTest;
scanf("%d", &nTest);
while (nTest--)
{
scanf("%d", &nK);
if (nK < 0)
{
nK *= -1;
}
//int nN = ceil(sqrt(2 * fabs(1.0 * nK) + 0.25) - 0.5 + 1e-9);
//上面那種方法存在浮點(diǎn)誤差,wa了三次
int nN = GetN(nK);
while (1)
{
if (((nN * nN + nN) / 2 - nK) % 2 == 0)
{
printf("%d\n", nN);
break;
}
++nN;
}
if (nTest)
{
printf("\n");
}
}
return 0;
}
說實(shí)話,這個題不是我親自推算出來。一直想到崩潰了,明知道只差一步,硬是無法想出來。實(shí)在想不出了,看了下別人解題報告上
的解釋。真的很慚愧很崩潰。。。這就是一個數(shù)列推理的題目吧。
給出一個數(shù)列ci(1<=ci<=n),然后給出數(shù)列ai中的a0和a(n+1)。并給出一個公式ai = ( a(i-1) + a(i+1) ) / 2 - ci。題目的意思
是讓求a1。大家在很久以前的高中時代一定做過很多的數(shù)列題,所以我一看到這個題還是感覺很親切的。然后就開始推算。我把上面那
個公式,從i==1到i==n,全部累加起來。消去2邊一樣的項(xiàng),得到一個結(jié)果
a1 + an = a0 + a(n+1) - 2 Σci(1<=i<=n)。從這
個公式,我只能得到a1和an 的和。想來想去都無法直接求出a1的值。但是,我也知道如果能求出a1,那么ai中的任何其它項(xiàng)都是能求
出來的。我猜想a1和an相等,提交當(dāng)然wa了。然后,我猜想ai是a0和a(n+1)的i分點(diǎn),提交還是wa了。后面這個猜想倒是合理點(diǎn),但是
還是有不嚴(yán)謹(jǐn)?shù)牡胤剑驗(yàn)槟菢樱琣1的值之和a0,a(n+1),c1這三個值有關(guān)系了。
這個題其實(shí)以前我想了一下,沒想出來。然后今天重新想的時候可能受以前的影響,限制了一個思路。那就是,再對式子a1 + an =
a0 + a(n+1) - 2 Σci(1<=i<=n)進(jìn)行累加。其實(shí),也有a1 + a(n-1) = a0 + an - 2 Σci(1<=i<=n-1)。這樣累加n次,剛好可以把
a2-an全部消去。可以得到,一個式子(n+1)a1 = n * a0 + a(n+1)- 2 ΣΣ cj(1<=j<=i) (1<=i<=n)。那么就可以直接求出a1了。
公式: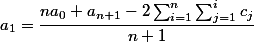
代碼如下:
#include <stdio.h>
#include <string.h>
int main()
{
int nCases;
int nN;
double a0, an1;
double a1;
double ci[3000 + 10];
double c;
double sum;
scanf("%d", &nCases);
while (nCases--)
{
scanf("%d", &nN);
scanf("%lf%lf", &a0, &an1);
sum = 0.0;
memset(ci, 0, sizeof(ci));
for (int j = 1; j <= nN; ++j)
{
scanf("%lf", &c);
ci[j] = ci[j - 1] + c;//ci[j]代表數(shù)列ci中第1-j項(xiàng)的和
sum += ci[j];
}
a1 = (nN * a0 + an1 - 2 * sum) / (nN + 1);
printf("%.2f", a1);
putchar('\n');
if (nCases)
{
putchar('\n');
}
}
return 0;
}
這又是一個數(shù)學(xué)題,不過我還是比較喜歡做這類數(shù)學(xué)雜題的。題目意思很簡單,給2個十進(jìn)制數(shù),n和b。如果用b進(jìn)制表示n!,
需要多少位數(shù),這個表示末尾會有多少個0。這個題并不需要什么高深的知識,這一點(diǎn)也是我喜歡做這類題的一個方法。
大家顯然都知道求n!用10進(jìn)制表示末尾會有多少個0的方法,就是求2*5最多有多少對。那么,b進(jìn)制了。方法類似,發(fā)散一下想法而已。
我還是先說求多少位數(shù)的方法吧。
b的m-1次 <= n!<= b的m次(PS,這個不等式如果把b換成10大家一定會明白的),
看到這個不等式應(yīng)該有想法了吧。兩邊同時取logb,就可以得到
Σlogi(1<=i<=n) <= m,m直接就求出來了。m即是位數(shù)。
再說怎么求末尾0的,發(fā)散下想法,我們也可以對n!中的每個因子試著求b的因子對,一共有多少對。但是,后面發(fā)現(xiàn)這樣不行,
因?yàn)楸热鏱是16,1和16是一對因子,2和8是一對因子,4和4是一對因子,也就是因?yàn)?也是4的因子,這樣計算因子對就會重復(fù)了。
但是對于b等于10的情況,可以例外而已。
呵呵,考慮其它的方法。求素數(shù)因子。任何數(shù)字都可以被分解為一些素數(shù)因子的乘積,這是毋容置疑的。那么,我們?nèi)シ纸鈔!中的
小于等于b的素數(shù)因子,并將其個數(shù)存儲在數(shù)組里面。然后死循環(huán)的去分解b的素數(shù)因子,能夠完全分解一次
(具體看下代碼,不好描述),ans就加1。否則,已經(jīng)沒有末尾0了。
雖然提交了16次才過。不過最后還算不錯吧,只用了0.508s。相比20s的時間界限,很小了。網(wǎng)上有些過的代碼,跑一個數(shù)據(jù)都要
幾分鐘。。。PS:uva上那些神人,怎么用0.0s算出來的,很難想象啊。
這個題目還有個很大的需要注意的地方,就是浮點(diǎn)數(shù)的精度問題。前面講到求位數(shù)需要用到log函數(shù),log函數(shù)的計算精度就出問題了。
最后需要對和加一個1e-9再floor才能過。特別需要注意這一點(diǎn),因?yàn)殚_始我的程序過了所有的http://online-judge.uva.es/board/viewtopic.php?f=9&t=7137&start=30上說的數(shù)據(jù)還是wa了。而且我還發(fā)現(xiàn)
log10計算精度高很多,如果log(這個是自然對數(shù))去計算,這個網(wǎng)站上的數(shù)據(jù)都過不了。
#include <stdio.h>
#include <string.h>
#include <math.h>
int nN, nB;
int nDivisor[1000];
int GetDigit(int nN, int nB)
{
double fSum = 0.0;
for (int i = 2; i <= nN; ++i)
{
fSum += log10(i);
}
fSum /= log10(nB);
return floor(fSum + 1e-9) + 1;
}
int GetZero(int nN, int nB)
{
memset(nDivisor, 0, sizeof(nDivisor));
for (int i = 2; i <= nN; ++i)
{
int nTemp = i;
for (int j = 2; j <= nTemp && j <= nB; ++j)//這樣循環(huán)就可以進(jìn)行素數(shù)因子分解了
{
while (nTemp % j == 0)
{
nDivisor[j]++;
nTemp /= j;
}
}
}
int nAns = 0;
while (1)
{
int nTemp = nB;
for (int j = 2; j <= nTemp; ++j)//分解nB
{
while (nTemp % j == 0)
{
if (nDivisor[j] > 0)//如果還可以繼續(xù)分解
{
--nDivisor[j];
}
else //直接可以goto跳出多重循環(huán)了
{
goto out;
}
nTemp /= j;
}
}
++nAns;
}
out:
return nAns;
}
int main()
{
while (scanf("%d%d", &nN, &nB) == 2)
{
int nDigit = GetDigit(nN, nB);
int nZero = GetZero(nN, nB);
printf("%d %d\n", nZero, nDigit);
}
return 0;
}
我們2個人和一個大二的小學(xué)弟,學(xué)弟以前沒有基礎(chǔ),完全處于復(fù)雜度還不會估計的醬油狀態(tài)。說實(shí)話,這次剛開始還不錯,1個半小時左右就出了2個題,當(dāng)時排在第8。也許這次的題有點(diǎn)難,其實(shí)也沒那么難,畢竟有人做出了8道題,而且是人,不是神。他們比我們強(qiáng)很多,雖然其余的隊(duì)基本多的就到4個題了。最悲劇的是,我們后面都沒有出題,I題和J題是最可能出的,還有那2個異或,如果勇敢的想下去做下去的話,也是可能的。說實(shí)話,還是得怪我,快2個星期沒怎么刷題了,就是忙這所謂的畢設(shè)。 我一直算那種想法比較好的,容易出想法,容易來靈感,但是這次真的也很好的反應(yīng)了我們的水平,還是非常不夠。這半年多的努力,學(xué)會了很多東西,但是更多的還是不會的東西。這半年來最幸運(yùn)的是,我的訓(xùn)練方法是正確的。其實(shí),也是因?yàn)槲冶旧砭褪窍雽W(xué)算法,不是急功近利的那種,所以,一直以來都不看解題報告,基本靠自己思考。ACM真的是一件有趣的事情,高中自然沒這個本事和運(yùn)氣基礎(chǔ)OI。大一就學(xué)了個C語言,大二學(xué)了點(diǎn)C++,Windows程序設(shè)計和數(shù)據(jù)結(jié)構(gòu)。大二暑假,訓(xùn)練了不到一個月的ACM,后面就一直處于醬油狀態(tài)了。其實(shí),我真的算想法還不錯的人,所以,我才一直對別人怎么想出我那些不會的題目感興趣。其實(shí),最有趣的東西應(yīng)該就是怎么想出這些東西來了。 我們隊(duì)最大的不足就是我們時間還比較短。看一下我寫過的acm代碼,還是從2011年11月6號開始的,而且最開始我還在寫百練上的那些程序設(shè)計導(dǎo)引上的代碼。從那個時候開始算OJ上過了的題量,即使算上參加的所有比賽,估計也不會超過200個,還有那么多的水題。。。有的時候,真的是一題見血,一題就給了我N多的啟發(fā)。看書基本也是從正月開始看的算導(dǎo),現(xiàn)在還有一部分沒看完。無論怎么樣,至少還有機(jī)會繼續(xù)搞下去。還有可能去參加區(qū)域賽,這就是最大的安慰。所有的其它事情,都可以放棄,但是ACM這次不能放棄,不能猶豫,不能妥協(xié)了。人無再少啊。。。 我其實(shí)也不是很喜歡計劃的那種,一般是做一個大致的期望,然后每天做一些事情朝那個方向努力。所幸的是,從大一學(xué)C語言開始,我就發(fā)現(xiàn),學(xué)編程,學(xué)計算機(jī)科學(xué),以及到現(xiàn)在的學(xué)算法,這些都是我喜歡的事情,連被英語單詞,我都覺得有意思了。所以,這樣下去也不錯,不至于無聊,并且有所收獲,而且朝著我的目標(biāo)。但是,這一次不能這樣了。僅僅這樣完全不夠,ACM應(yīng)該需要點(diǎn)其它的東西,需要那種更強(qiáng)大的付出然后那種不計回報的堅持吧。應(yīng)該說過程就是最大的收獲了,即使最后連個紀(jì)念獎都沒有。。。紀(jì)念獎應(yīng)該都有,不至于擔(dān)心。。。
剛剛ACM校賽頒獎了,還是二等獎,本來是滿懷期待去領(lǐng)一等獎的。。。校內(nèi)第四名,整個第八名。。。基本上已經(jīng)盡了了,第3個小時40分鐘左右還是校內(nèi)第二的,出了5道題。。。最后沒有出題了。有一個是網(wǎng)絡(luò)流的題,因?yàn)椴皇煜]寫。讓寫了其它題,那個題據(jù)說是騰訊的面試題。比較麻煩,不好過。那個題估計題目數(shù)據(jù)比較弱,被人爆了。因?yàn)楹竺嫦胂氤鲱}人的說的一個解法不是很嚴(yán)謹(jǐn)。無論怎么樣,第三年參加校賽還是沒有拿一等獎。這一次,我沒有在打醬油了。。。準(zhǔn)備了近半年,還是弄得個這樣的結(jié)果。。。唉。。。 從去年騎車去崀山回來之后,基本絕大部分時間都放在學(xué)算法上面了。poj百練刷了100道左右的題,uva上面50道左右的題。最重要的是,我沒有看一個解題報告,我全部是自己想出來A掉的。。。今年開始看的算法導(dǎo)論,到現(xiàn)在基本快看完網(wǎng)絡(luò)流了,雖然圖論看得不怎么樣,也沒做些什么訓(xùn)練。大二大三就沒有認(rèn)真搞過ACM,當(dāng)時以為一定會去工作,c++和vc桌面開發(fā)學(xué)得比較多,時間散開得比較范。以前一直處于打醬油中,只有大二暑假集訓(xùn)做了一定量的題。因?yàn)楸荣惾チ艘欢ù螖?shù),一直被虐中,心里也從沒放棄過ACM。既然保研了,最有意義的事情就只能是ACM了。從那個時候起,宅了半年吧。這學(xué)期畢業(yè)設(shè)計一點(diǎn)也沒做,就交了報告。唉,尤其這學(xué)期真的很揪心啊。畢設(shè)搞不好會做得很爛,上次中期檢查0%的進(jìn)度。過幾天又得重新檢查了。這一段時間的希望都一直寄托在校賽上面,拿一個一等獎,也對得起當(dāng)了這么多次水軍了。想不到,唉。。。真不知道,大學(xué)這么幾年都干了些什么。。。
最近一直沒跟很多人聯(lián)系,對不住了,我一直都很宅,不過我一直都把你們都朋友。。。打算搞定畢設(shè)后繼續(xù)ACM,一直到秋季區(qū)域賽全部結(jié)束,至死方休吧,暑期留校集訓(xùn),然后繼續(xù)留校刷題吧,一直刷到區(qū)域賽,把題量刷到300(寧肯刷水題也不允許刷解題報告)吧。有此打算學(xué)弟們,可以跟我和吳尚聯(lián)系。如果區(qū)域賽再連個銅獎都拿不回來,會遺憾終生的。。。
謹(jǐn)以此文祭奠我悲催的ACM歷程!!!

 Fig: A 4x4 Grid Fig: A 4x4x4 Cube
Fig: A 4x4 Grid Fig: A 4x4x4 Cube 這是一道數(shù)學(xué)題吧。想清楚之后就發(fā)現(xiàn)就是求累加和。
問題是給定一個正方形(體,超體),求其中的所有的正方形(體,超體),長方形(體,超體)。 比如,4 * 4的正方形中,有14個正方形,
22個長方形,4 * 4 * 4的立方體中有36個正方體,180個長方體。依次類推,超正方體指的是四維空間。
觀察一下一個4*4正方形中,仔細(xì)驗(yàn)證一下就會發(fā)現(xiàn),正方形的個數(shù)是 Σ(4 - i + 1) * (4 - i + 1)(其中i從1到4),長方形的個數(shù)是
Σ(4 - i + 1) (其中j從1到4) * Σ(4 - j + 1)(其中j從1到4)。如果變成3維的就多一層k,k也從1變化到4。如果變成4維的就再多一層l,
l也從1變化到4。
然后變換一下,就可以得到s2(n) = 1^1 + 2^2 + ... + n^n,s3(n)則是對立方的累加和,s4(n)則是對四次方的累加和。
再計算r2(n)。可以先把正方形包括在內(nèi)計算出所有的和。那么r2(n) = Σ(n - i + 1) * Σ(n - j + 1) - s2(n)。如果直接進(jìn)行這個式子
的求和話很復(fù)雜。再觀察一下這個式子,因?yàn)閚 - i + 1的變化范圍就是1到n,那么上面的式子可以變化為 r2(n) = ΣΣi * j - s2(n)。
意思是求i*j的和,i和j都是從1變化到n。很簡單就可以得到r2(n) = pow(n * (n + 1) / 2, 2) - s2(n)。同樣的求和可以得到,
r3(n) = pow(n * (n + 1) / 2, 3) - s3(n)。r4(n) = pow(n * (n + 1) / 2, 4) - s4(n)。
另外如果不知道平方和,立方和,四次方和的公式,也可以迭代計算,復(fù)雜度也是O(100)。這樣的話,根本不需要使用這些難記憶的公式了。
代碼如下:
#include <stdio.h>
#include <math.h>
unsigned long long s2[101];
unsigned long long r2[101];
unsigned long long s3[101];
unsigned long long r3[101];
unsigned long long s4[101];
unsigned long long r4[101];
int main()
{
unsigned long long i = 0;
while (i <= 100)
{
s2[i] = i * (i + 1) * (2 * i + 1) / 6;//平方和
s3[i] = i * i * (i + 1) * (i + 1) / 4;//立方和
s4[i] = i * (i + 1) * (6 * i * i * i + 9 * i * i + i - 1) / 30;//四次方和
r2[i] = pow(i * (i + 1) / 2, 2) - s2[i];
r3[i] = pow(i * (i + 1) / 2, 3) - s3[i];
r4[i] = pow(i * (i + 1) / 2, 4) - s4[i];
++i;
}
int nN;
while (scanf("%d", &nN) != EOF)
{
//printf("%I64u %I64u %I64u %I64u %I64u %I64u\n", s2[nN], r2[nN], s3[nN], r3[nN], s4[nN], r4[nN]);
printf("%llu %llu %llu %llu %llu %llu\n", s2[nN], r2[nN], s3[nN], r3[nN], s4[nN], r4[nN]);
}
return 0;
}
http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=99&page=show_problem&problem=1731 這是一個數(shù)學(xué)題,比較有意思。題意大致是:有2條平行的直線,第一條上面有m個點(diǎn),第二條上面有n個點(diǎn)。那么連接這寫點(diǎn)能產(chǎn)生m*n
條直線(不包括和原來的執(zhí)行平行的直線)。問這m*n直線最多有多少個內(nèi)交點(diǎn)(意思是不屬于原來m,n個點(diǎn)的交點(diǎn))...

想來想去,推理了1個多小時才出來正式結(jié)果。感覺比較有意思,寫篇博文記錄下。我先是從反面排除,想了試了好久到最后還是發(fā)現(xiàn)無法
排除干凈。。。最后只能從正面開始求證了。我這樣定義一條執(zhí)行(i,j),其中i代表在第一條直線中的端點(diǎn),j代表在第二條直線中的端點(diǎn)。
顯然1 <= i <= m,而且1 <= j <= n。
現(xiàn)在的話只要求出和直線(i,j)相加的直線有多少條,然后對i,j進(jìn)行累加求和。再對和除以2就能得到答案了。
那么有多少條直線能和直線(i,j)相交了。很顯然,和(i,j)相交的直線的端點(diǎn)必須在其兩側(cè)。意思是在第一條直線中的端點(diǎn)范圍為
[1, i - 1],在第二條直線中的端點(diǎn)范圍為[j + 1, n],總結(jié)(i - 1) * (n - j) 條直線。但是還有第二種情況,在第一條直線中的端點(diǎn)范圍
為[i + 1, m], 在第二條直線中的端點(diǎn)范圍為[1, j - 1],總結(jié)(m - i) * (j - 1) 條直線。
總計sum = i * n + i - m -n + j (m - 2 * i + 1) 條直線。
再求
Σsum(j從1到n)得到和式(m*n*n - m*n - n*n + n) / 2,再對這個式子進(jìn)行i從1到m的累加。因?yàn)闆]有i了,其效果就是乘以m。
然后最終的和除以2,所以最后的表達(dá)式是(m*m*n*n - m*m*n - m*n*n + m*n) / 4。這個式子顯然是關(guān)于m,n對稱的。
這一點(diǎn)也可以驗(yàn)證這個式子的正確性。
程序?qū)懫饋砭秃芎唵瘟耍a如下:
#include <iostream>
using namespace std;
int main()
{
long long m, n;
int nCases = 0;
while (cin >> m >> n, m + n != 0)
{
long long a = m * m;
long long b = n * n;
cout << "Case " << ++nCases << ": "
<< (a * b - a * n - b * m + m * n) / 4 << endl;
}
return 0;
}
這是一道很簡單的題吧,大數(shù)都不需要用到,可是很悲劇wa了很久。確實(shí)寫題太不嚴(yán)謹(jǐn)了,出了好多bug,甚至題意都沒注意清楚。
這種題我一直忘記忽略前導(dǎo)'0'。
還有題目沒有給出最長的數(shù)字的長度,所以最好用string類。
使用longlong之前最好已經(jīng)測試了OJ,是用%lld還是%I64d,如果OJ后臺是linux下的g++,只能是%lld,Windows下的MinGW32
(Dev-C++也一樣用的是這個庫)要用%I64d才能正確。所以預(yù)賽之前需要對普通題進(jìn)行測試下。
還有注意復(fù)合邏輯表達(dá)式是否寫正確了,最近經(jīng)常寫錯了,太郁悶了。
給自己提個醒吧,校賽這種題再不能迅速A掉基本太丟人了。
代碼如下:
#include <stdio.h>
#include <limits.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define MAX (10000)
char szIntMax[20];
char szLine[MAX];
char szOne[MAX];
char szTwo[MAX];
char szOper[10];
char* MyItoa(int nNum, char* pszNum, int nBase)
{
int nLen = 0;
while (nNum)
{
pszNum[nLen++] = nNum % nBase + '0';
nNum /= nBase;
}
reverse(pszNum, pszNum + nLen);
pszNum[nLen] = '\0';
return pszNum;
}
bool IsBigger(char* pszOne, int nLenOne, char* pszTwo, int nLenTwo)
{
//printf("pszOne:%s, pszTwo:%s\n", pszOne, pszTwo);
if (nLenOne != nLenTwo)
{
return nLenOne > nLenTwo;
}
else
{
for (int i = 0; i < nLenOne; ++i)
{
if (pszOne[i] != pszTwo[i])
{
return pszOne[i] > pszTwo[i];
}
}
return false;
}
}
int StripHeadZero(char* pszNum)
{
int nLen = strlen(pszNum);
int i;
for (i = 0; i < nLen && pszNum[i] == '0'; ++i);
if (i == nLen)
{
pszNum[0] = '0';
pszNum[1] = '\0';
nLen = 2;
}
else
{
char* pszWrite = pszNum;
char* pszRead = pszNum + i;
nLen = 0;
while (*pszRead)
{
*pszWrite++ = *pszRead++;
++nLen;
}
*pszWrite = '\0';
}
return nLen;
}
int main()
{
int nIntMax = INT_MAX;
MyItoa(nIntMax, szIntMax, 10);
int nLenMax = strlen(szIntMax);
while (gets(szLine))
{
if (szLine[0] == '\0')
{
continue;
}
sscanf(szLine, "%s%s%s", szOne, szOper, szTwo);
printf("%s %s %s\n", szOne, szOper, szTwo);
StripHeadZero(szOne);
StripHeadZero(szTwo);
int nLenOne = strlen(szOne);
int nLenTwo = strlen(szTwo);
bool bFirst = false;
bool bSecond = false;
if (IsBigger(szOne, nLenOne, szIntMax, nLenMax))
{
printf("first number too big\n");
bFirst = true;
}
if (IsBigger(szTwo, nLenTwo, szIntMax, nLenMax))
{
printf("second number too big\n");
bSecond = true;
}
if (bFirst || bSecond)
{
if (szOper[0] == '+' || (szOper[0] == '*' && szOne[0] != '0' && szTwo[0] != '0'))
{
printf("result too big\n");
}
}
else
{
long long nOne, nTwo;
sscanf(szLine, "%lld%s%lld", &nOne, szOper, &nTwo);
long long nResult;
if (szOper[0] == '+')
{
nResult = nOne + nTwo;
}
else if (szOper[0] == '*')
{
nResult = nOne * nTwo;
}
//printf("%I64d\n", nResult);
if (nResult > INT_MAX)
{
printf("result too big\n");
}
}
}
return 0;
}
這個題,粗看之下還沒怎么看懂,這個應(yīng)該跟我英語水平有關(guān)系。然后再看輸入輸出,漸漸的才明白什么意思。原來是要把2*N張破紙組合
成N張一樣的紙。我歷來思維比較隨便,不是很嚴(yán)謹(jǐn)?shù)哪欠N。然后,想了一下發(fā)現(xiàn)一定會有大于等于N張破紙片是符合前半部分模式的。
那么,可以建一個字典樹,把所有的是前半張紙的找出來。然后根據(jù)這前半張紙,找出剩下的后半張紙(因?yàn)橹酪徽麖埣埖拈L度,所以知道
剩下的半張紙的長度)。但是寫出來就發(fā)現(xiàn)這樣不嚴(yán)謹(jǐn),是不對的。因?yàn)閱渭兏鶕?jù)已經(jīng)找出來的前半張紙,無法確定后半張紙(事實(shí)上,只能
確定其長度而已)。
那么只能找其它方法了,再檢查了下數(shù)據(jù)范圍,發(fā)現(xiàn)比較小,那么意味著可以暴力求解了。好吧,那就深搜吧。我把所有的破紙片按照它們
的長度分成一些集合,對于長度為len的紙片集合,只要與長度為nAnsLen - len的紙片集合進(jìn)行搜索匹配,找出一個可行的解即可了。我又
想當(dāng)然的認(rèn)為只要匹配一對集合即可了,那么很顯然又是錯的了。好吧,我只能對所有集合進(jìn)行匹配了。對每一對集合進(jìn)行深搜回溯來匹配待
選的Ans,而這個Ans是從第一對集合中搜索出來的答案。
代碼寫得很冗長,很復(fù)雜,差不多200多行了。真的是水平有限,這種題很明顯應(yīng)該有更方便的解法的,而且我的代碼應(yīng)該不至于寫得這么
亂的。
后面還是錯了很多次,發(fā)現(xiàn)了很多bug,比如我如果搜索長度為nAnsLen/2的集合時就必須進(jìn)行特殊處理。還有最后一個樣例后面不能輸
出’\n',而且uvaoj不能對這個換行判PE,一直是WA,實(shí)在是讓人崩潰。
#include <stdio.h>
#include <string.h>
#define MAX (256 + 10)
#define MAX_NUM (150)
char szLines[MAX_NUM][MAX];
char szAns[MAX];
struct SET
{
int nNum;
char szLines[MAX_NUM][MAX];
bool bUsed[MAX];
};
SET sets[MAX];
char szTmpOne[MAX];
char szTmpTwo[MAX];
int nAnsLen;
bool bFind;
void dfs(int nI, int nNum)
{
if (nNum == 0)
{
bFind = true;
}
else
{
for (int i = 0; i < sets[nI].nNum && !bFind; ++i)
{
for (int j = 0; j < sets[nAnsLen - nI].nNum && !bFind; ++j)
{
if (nI == nAnsLen - nI && i == j)
{
continue;
}
if (!sets[nI].bUsed[i] && !sets[nAnsLen - nI].bUsed[j])
{
strcpy(szTmpOne, sets[nI].szLines[i]);
strcat(szTmpOne, sets[nAnsLen - nI].szLines[j]);
strcpy(szTmpTwo, sets[nAnsLen - nI].szLines[j]);
strcat(szTmpTwo, sets[nI].szLines[i]);
//printf("%s\n", szAns);
if (strcmp(szTmpOne, szAns) == 0 || strcmp(szTmpTwo, szAns) == 0)
{
sets[nI].bUsed[i] = sets[nAnsLen - nI].bUsed[j] = true;
if (!bFind)
{
if (nI == nAnsLen - nI)
{
dfs(nI, nNum - 2);
}
else
{
dfs(nI, nNum - 1);
}
}
sets[nI].bUsed[i] = sets[nAnsLen - nI].bUsed[j] = false;
}
}
}
}
}
}
bool Find(int nI)
{
bFind = false;
for (int i = 0; i < sets[nI].nNum && !bFind; ++i)
{
for (int j = 0; j < sets[nAnsLen - nI].nNum && !bFind; ++j)
{
if (nI == nAnsLen - nI && i == j)
{
continue;
}
sets[nI].bUsed[i] = true;
sets[nAnsLen - nI].bUsed[j] = true;
strcpy(szAns, sets[nI].szLines[i]);
strcat(szAns, sets[nAnsLen - nI].szLines[j]);
if (nI == nAnsLen - nI)
{
dfs(nI, sets[nI].nNum - 2);
}
else
{
dfs(nI, sets[nI].nNum - 1);
}
if (bFind)
{
for (int k = nI + 1; k <= nAnsLen / 2; ++k)
{
bFind = false;
dfs(k, sets[k].nNum);
if (!bFind)
{
break;
}
}
if (bFind)
{
return true;
}
}
strcpy(szAns, sets[nAnsLen - nI].szLines[j]);
strcat(szAns, sets[nI].szLines[i]);
if (nI == nAnsLen - nI)
{
dfs(nI, sets[nI].nNum - 2);
}
else
{
dfs(nI, sets[nI].nNum - 1);
}
if (bFind)
{
for (int k = nI + 1; k <= nAnsLen / 2; ++k)
{
bFind = false;
dfs(k, sets[k].nNum);
if (!bFind)
{
break;
}
}
if (bFind)
{
return true;
}
}
sets[nI].bUsed[i] = false;
sets[nAnsLen - nI].bUsed[j] = false;
}
}
return false;
}
void Search()
{
for (int i = 0; i <= nAnsLen; ++i)
{
if (sets[i].nNum)
{
Find(i);
break;
}
}
}
int main()
{
int nCases;
#ifdef CSU_YX
freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
#endif
scanf("%d\n", &nCases);
int nNum = 0;
int nTotalLen = 0;
while (gets(szLines[nNum]), nCases)
{
if (szLines[nNum][0] == '\0' && nNum != 0)
{
nAnsLen = nTotalLen * 2 / nNum;
memset(szAns, 0, sizeof(szAns));
Search();
printf("%s\n\n", szAns);
memset(sets, 0, sizeof(sets));
memset(szLines, 0, sizeof(szLines));
nNum = 0;
nTotalLen = 0;
--nCases;
}
else if (szLines[nNum][0] != '\0')
{
int nLen = strlen(szLines[nNum]);
nTotalLen += nLen;
strcpy(sets[nLen].szLines[sets[nLen].nNum], szLines[nNum]);
++sets[nLen].nNum;
++nNum;
}
}
return 0;
}
這是算法導(dǎo)論習(xí)題11.1-4。
具體題目如下:
組實(shí)現(xiàn)直接尋址hash.jpg)
解決該題目的要點(diǎn):
1.由于是無窮大的數(shù)組,所以無法事先初始化該數(shù)組。
2.所提供的方案必須是O(1)。
3.使用的額外空間只能是O(n),這樣平均到每一個項(xiàng)上的空間都是O(1)。
一時之間好像沒有一點(diǎn)頭緒,在幾個群里面發(fā)問了,網(wǎng)上搜了很久也沒有找到答案,后面一群里有個高人給了個鏈接,里面有解法。
鏈接地址:http://www.cnblogs.com/flyfy1/archive/2011/03/05/1971502.html,這篇文章里面另外給了個pdf,這個pdf估計是解法
的來源。偽代碼寫得不給力,不過前面的英文描述卻很清晰。說實(shí)話,這個方法很巧妙。
解法大概的意思如下:
開一個額外的數(shù)組A,A[0]表示A數(shù)組元素的數(shù)目(當(dāng)然不包括A[0]本身),A[i]代表插入的第i個元素的key。假設(shè)原來的無窮大數(shù)組用Huge
表示,如果Huge[i](直接尋址,假設(shè)i就是key)有效,則表示其在A數(shù)組中的索引。那么如果A[Huge[i]] == i 而且 Huge[i] <= A[0] &&
Huge[i] > 0,則表示i這個位置已經(jīng)有元素插入了。
插入:A[0]++;A[A[0]] = key; Huge[key] = A[0];
搜索: A[Huge[i]] == i && Huge[i] <= A[0] && Huge[i] > 0 則return true;
刪除: 先搜索該位置是否有元素, 如果Search(key)成功,則先把Huge[ A[A[0]] ] = Huge[key],
然后交換A[A[0]]和A[Huge[key]],A[0]--即可。
所有操作都是O(1),平均到每一個項(xiàng),使用的空間都是O(1)。
我用代碼實(shí)現(xiàn)的模擬如下:
#include <stdio.h>
#include <vector>
#include <algorithm>
using std::swap;
using std::vector;
#define INF (100)
int nHuge[INF];
//假設(shè)這個巨大的數(shù)組是無法初始化的
vector<
int> vA;
void Init()
{
vA.push_back(0);
//添加A[0]表示元素的數(shù)目
}
void Insert(
int nKey)
{
vA[0]++;
nHuge[nKey] = vA[0];
vA.push_back(nKey);
}
bool Search(
int nKey)
{
if (nHuge[nKey] > 0 && nHuge[nKey] <= vA[0] && vA[nHuge[nKey]] == nKey)
{
return true;
}
return false;
}
void Delete(
int nKey)
{
if (Search(nKey))
{
nHuge[ vA[vA[0]] ] = nHuge[nKey];
//將huge的最后一個元素中存儲的A數(shù)組的索引改為nHuge[nKey]
swap(vA[vA[0]], vA[nHuge[nKey]]);
//交換key
--vA[0];
vA.erase(vA.end() - 1);
}
}
#define MAX (10)
int main()
{
Init();
int i;
for (i = 0; i < MAX; ++i)
{
Insert(i);
}
for (i = 0; i < MAX; ++i)
{
printf("Search:%d %s\n", i, Search(i) ==
true? "Success" : "Failure");
}
printf("\n");
Delete(4);
Delete(9);
Delete(1);
for (i = 0; i < MAX * 2; ++i)
{
printf("Search:%d %s\n", i, Search(i) ==
true? "Success" : "Failure");
}
return 0;
}