PKU 2941
這道題需要動一下腦筋，屬于數(shù)學題。
問題描述：給一個n×n的矩陣，如果從每行各拿出一個元素，且這些元素的列指標都不同，即



其中是的一個排列。
如果任何這樣一個元素的和都相等，則稱這個矩陣是homogeneous的。

題目要求任給一個n維矩陣,1<=n<=1000，判斷它是否是homogeneous的。

如果直接做，即求出所有的然后求和，這樣的復雜度為n!，這是無法接受的。

下面給出一個算法，能在時間內(nèi)判斷出來。設n維矩陣A，現(xiàn)為A加上一行跟一列，使A變成n+1維的。



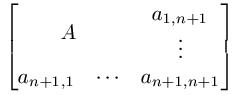
Theorem 1 

若n維矩陣A是homogeneous的，則劃去A的任一行與任一列，剩下的n-1維矩陣是homogeneous的。

Proof
設劃去的是第x行第y列，剩下的矩陣若不是homogeneous的，則存在與，這兩個序列的和不等，那么都加上，可以得到矩陣A的兩個序列，這兩個序列的和不等，即A不是homogeneous的，與假設矛盾。

Theorem 2
若Homogeneous的A增廣后的矩陣B是Homogeneous的，則對于A中任意元素 ，必有

Proof
這個等式的意義是在A取元素，在新矩陣取，其余任取，這么一個序列的和必須等于在新矩陣中取跟，其余任取所得的序列的和。注意到任取那部分是在A劃去行i，列j后的子矩陣中取的。由于B是Homogeneous，任何合法序列的和都相等，若題設的等式不成立，則任取這一部分也不相等（這樣才可能使得所有B包含的序列的和都相等）。但A是Homogeneous的，任取這一部分不可能不等，矛盾。

有了上面的定理2，算法就很簡單，看下面的代碼：