離上一篇已經有近兩個月的時間了,這段時間事情煩(多),導致沒心情寫,現在爭取補上。
生成epsilon-NFA
epsilon-NFA是包含epsilon邊(空邊)的NFA,把簡單正則表達式轉換成epsilon-NFA的方法如下:
正則表達式:”ab” 對應的epsilon-NFA是:
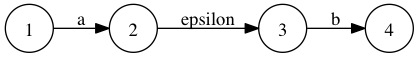
正則表達式:”a|b”對應的epsilon-NFA是:
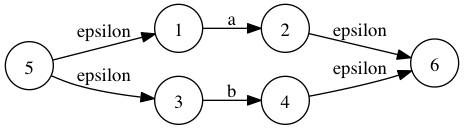
正則表達式:”a*” 對應的epsilon-NFA是:
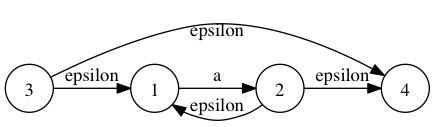
這是最基本的3種正則表達式的NFA表示,其中a*在實際的正則表達式實現中通常生成的epsilon-NFA不是這樣的,因為有下面這些正則表達式存在:
a{m} 重復a,m次
a{m,n} 重復a,m到n次
a{m,} 重復a,至少m次
a+ 重復a,至少1次
a? 重復a,0次或1次
所以對于a*表示重復至少0次的實現可以跟上面這些正則表達式采用相同方法的實現。
按照這些生成規則就可以把正則表達式轉換成epsilon-NFA,我代碼中即把這些生成規則實現成一個AST的visitor。
epsilon-NFA subset construction to DFA
在生成了epsilon-NFA之后,通常會有很多epsilon的邊存在,也會有很多無用的state存在,所以通常需要把epsilon邊消除并合并state,這個過程采用的算法是subset construction,如下:
subset construction:
start_subset <- epsilon_extend(start_state) // 把start_state通過epsilon擴展得到起始subset
subsets <- { start_subset } // 初始化subsets
work_list <- subsets // 初始化work_list
while (!work_list.empty())
{
subset <- work_list.pop_front()
for edge in epsilon-NFA // 取出NFA中的每條邊
{
next_subset <- delta(subset, edge) // 對subset中的每個state通過edge所到達的state的epsilon邊擴展得到next_subset
if (!subsets.exist(next_subset)) // 如果next_subset不存在于subsets中,則把這個next_subset加入到work_list中
work_list.push_back(next_subset)
map[subset, edge] = next_subset // 構建subset到next_subset的邊映射
subsets.merge({next_subset}) // 把next_subset合并到subsets
}
}
delta:
next_subset <- { } // 初始化next_subset為空集合
for state in subset
{
// 取出next_state并將它通過epsilon邊擴展得到的subset合并到next_subset中
next_state <- map[state, edge]
if (next_state)
next_subset.merge(epsilon_extend(next_state))
}
這里面使用了epsilon_extend,它是把一個state的所有epsilon邊能到達的state構成一個集合,比如上面正則表達式a*對應的epsilon-NFA中的所有state的epsilon_extend是:
epsilon_extend(1) –> { 1 }
epsilon_extend(2) –> { 1, 2, 4 }
epsilon_extend(3) –> { 1, 3, 4 }
epsilon_extend(4) –> { 4 }
對于一個epsilon-NFA來說,每個state的epsilon_extend是固定的,因此可以對epsilon-NFA中的每個state都求出epsilon_extend并保存下來,算法如下:
epsilon_extend_construct:
work_list <- { }
// 為每個state初始化epsilon_extend集合
for state in epsilon-NFA
{
epsilon_extend(state) <- { state }
work_list.push_back(state)
}
while (!work_list.empty())
{
state <- work_list.pop_front()
state_epsilon_extend <- epsilon_extend(state)
// 把state通過epsilon所能到達的state的epsilon_extend
// 合并到當前state的epsilon_extend
for next_state in map[state, epsilon]
state_epsilon_extend.merge(epsilon_extend(next_state))
// 如果當前state的epsilon_extend變化了之后
// 把所有通過邊epsilon到達state的pre_state都加入到work_list中
if (state_epsilon_extend.has_changed())
{
for pre_state in epsilon_pre(state)
work_list.push_back(state)
}
}
epsilon-NFA通過subset construction構造成完之后,并把構造的subsets中的subset轉換成DFA中的state,再把NFA中除epsilon邊之外的所有邊都轉換成DFA的邊,這樣就把DFA構造完成。
DFA minimization
從NFA構造完成DFA之后,這時的狀態數量一般不是最少的,為了減少最終生成的狀態機的狀態數量,通常會對DFA的state進行最小化構造,這個算法具體如下:
minimization:
// 把所有state劃分成accept的state集合和非accept的state集合
state_sets <- { {accept_state(DFA)}, {non_accept_state(DFA)} }
do
{
work_list <- state_sets
old_state_sets_size <- state_sets.size()
state_sets <- { }
for state_set in work_list
{
split_success <- false
for edge in DFA
{
// 如果edge可以把state_set拆分成兩個subset,那就把新拆分出來的
// 兩個subset合并到state_sets里面,并break繼續work_list中取出下一個
// state_set拆分
subset1, subset2, split_success <- split(state_set, edge)
if (split_success)
{
state_sets.merge({subset1, subset2})
break
}
}
if (!split_success)
state_sets.merge({state_set})
}
} while (old_state_sets_size != state_sets.size())
這里面的split是把一個state_set按edge劃分成兩個subset,即對于state_set中的每一個state都通過這條邊edge到達的state屬于不同的state_set時就把state_set拆分成兩個subset。首先把第一個state劃分到subset1中,從第二個state開始通過邊edge到達的state所屬的state_set和第一個state通過邊edge到達的state所屬的state_set為同一個的時候,把這個state劃分到subset1中,否則劃分到subset2中。
這個算法就這樣依次把最初的兩個state_set(accept的state組成的set和非accept的state組成的set)劃分到不能再劃分為止,此時就把能合并的state都合并到了同一個state_set中,這時只需要把每個state_set轉換成最終狀態機中的state,即可完成DFA的最小化構造并轉換成狀態機。得到狀態機之后,就可以使用狀態機進行字符匹配了。