關于擴展的卡特蘭數：
1.(n-m+1)/(n+1)*c(n+m,n)
2.c[n+m][n]-c[n+m][m-1]
Catalan，Eugene，Charles，卡特蘭（1814～1894）比利時數學家，生于布魯日（Brugge），早年在巴黎綜合工科學校就讀。1856年任列日（Liege）大學數學教授，并被選為比利時布魯塞爾科學院院士。
卡特蘭一生共發(fā)表200多種數學各領域的論著。在微分幾何中，他證明了下述所謂的卡特蘭定理：當一個直紋曲線是平面和一般的螺旋面時，他只能是實的極小曲面。他還和雅可比（Jacobi，C·G·J）同時解決了多重積分的變量替換問題，建立了有關的公式。
1842年，他提出了一種猜想：方程xz－yt＝1沒有大于1的正整數解，除非平凡情形32－23＝1。這一問題至今尚未解決。
（mathoe注：即除了8、9這兩個連續(xù)正整數都是正整數的方冪外，沒有其他。1962年我國數學家柯召以極其精湛的方法證明了不存在三個連續(xù)正整數，它們都是正整數的方冪，以及方程x2－yn＝1，n＞1，xy≠0無正整數解。并且還證明了如果卡特蘭猜想不成立，其最小的反例也得大于1016。）
此外，卡特蘭還在函數論、伯努利數和其他領域也做出了一定的貢獻。
卡特蘭通過解決凸n邊形的剖分得到了數列Cn。
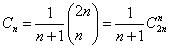
凸n＋2邊形用其n－1條對角線把此凸n＋2邊形分割為互不重疊的三角形，這種分法的總數為Cn。
為紀念卡特蘭，人們使用“卡特蘭數”來命名這一數列。
據說有幾十種看上去毫不相干的組合計數問題的最終表達式都是卡特蘭數的形式。
卡特蘭數在數學競賽、信息學競賽、組合數學、計算機編程等都會有其不同側面的介紹。
前幾個卡特蘭數：規(guī)定C0＝1，而
C1＝1，C2＝2，C3＝5，C4＝14，C5＝42，
C6＝132，C7＝429，C8＝1430，C9＝4862，C10＝16796，
C11＝58786，C12＝208012，C13＝742900，C14＝2674440，C15＝9694845。
遞推公式
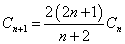
圓周上有標號為1，2，3，4，……，2n的共計2n個點，這2n個點配對可連成n條弦，且這些弦兩兩不相交的方式數為卡特蘭數Cn。
2003年浙江省小學數學夏令營競賽考了這個題：圓周上10個點可以連成既不相交，也沒有公共端點的5條線段，不同的連法共有_____種。
答：方法的種數是卡特蘭數C5＝42，此題被收錄進單墫主編的知識出版社出版的《華數奧賽強化訓練》小學六年級冊的“計數問題”專題。
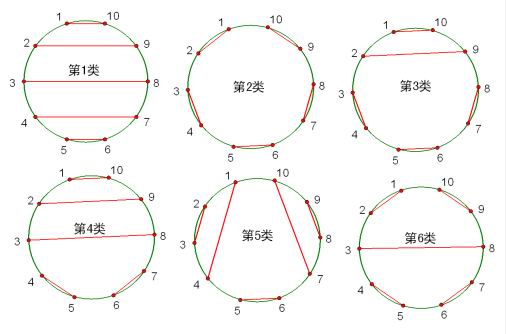
共六種類型，第1類有5種連法，第2類有2種連法，第3類有10種連法，第4類有10種連法，第5類有10種連法，第6類有5種連法。共有42種連法。
1994年《小學數學》有獎征答競賽：游樂園門票1元一張，每人限購一張。現在有10個小朋友排隊購票，其中5個小朋友每人只有1元的鈔票一張，另5個小朋友每人只有2元的鈔票一張，售票員沒有準備零錢。問：有多少種排隊方法，使售票員總能找的開零錢？
（此題也被許多奧數資料收錄為例題或習題，《華羅庚學校數學課本》小學六年級冊的思維訓練也收有此題）
答：現把拿1元的5個小朋友看成是相同的，把拿2元的5個小朋友也看成是相同的，使用我們常用的“逐點累加法”：
圖中每條小橫段表示拿1元的小朋友，每條小豎段表示拿2元的小朋友，要求從A走到B的過程中網格中任何點均有橫段數不小于豎段數：拿1元的要先，且人數不能少于拿2元的，即不能越過對角線AB：每個點所標的數即為從A走到此點的方法數。求從A到B的走法的方法數。逐點累加可求出為42，即卡特蘭數C5＝42。
又由于每個小朋友是不相同的，所以共有42×5！×5！＝42×120×120＝604800種情況。
若把此題的10個人，拿1元的有5人，拿2元的有5人改為共有2n個人，拿1元的n人，拿2元的n人，則符合要求的排隊方法數為：
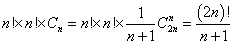
再一個卡特蘭數的例子：
甲乙兩人比賽乒乓球，最后結果為20∶20，問比賽過程中甲始終領先乙的計分情形的種數。
即甲在得到1分到19分的過程中始終領先乙，其種數是卡特蘭數
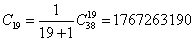
再一個卡特蘭數的例子
飯后，姐姐洗碗，妹妹把姐姐洗過的碗一個一個放進碗櫥摞成一摞。一共有n個不同的碗，洗前也是摞成一摞的，也許因為小妹貪玩而使碗拿進碗櫥不及時，姐姐則把洗過的碗摞在旁邊，問：小妹摞起的碗有多少種可能的方式？
答：得數是第n個卡特蘭數Cn。
再一個卡特蘭數的例子
一個汽車隊在狹窄的路面上行駛，不得超車，但可以進入一個死胡同去加油，然后再插隊行駛，共有n輛汽車，問共有多少種不同的方式使得車隊開出城去？
答：得數是第n個卡特蘭數Cn。
卡特蘭數
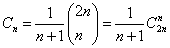
求證：卡特蘭數Cn是整數。
證明：
①取整函數不等式：對任意實數x，y有[x＋y]≥[x]＋[y]。這里[x]表示不大于實數x的最大整數。
解：由定義x≥[x]……（1）
y≥[y]……（2）以上兩式相加，得：x＋y≥[x]＋[y]，
把上式再取整，得：[x＋y]≥[[x]＋[y]]＝[x]＋[y]，即[x＋y]≥[x]＋[y]。
②1000！的末尾0的個數249個。（現在有的小學奧數書上出現了100！末尾有幾個零的題目：24個）
解：1000÷5＝200，
200÷5＝40，
40÷5＝8，
8÷5＝1……3
以上各商相加，即得1000！末尾0的個數＝200＋40＋8＋1＝249個。
③n！的質因數分解式中質因子p的冪次數：
…………（1）
k！的質因數分解式中質因子p的冪次數
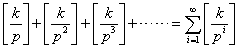…………（2）
(n－k)!的質因數分解式中質因子p的冪次數
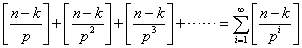…………（3）
這里寫成西格馬求和式時使用了無窮的形式，但是從某一確定項之后的每項都是0，為了統一，都寫成了“∞”形式。
④組合數是整數
解：
⑤卡特蘭數是整數
⑥卡特蘭數是整數的另外一個證明
④組合數是整數
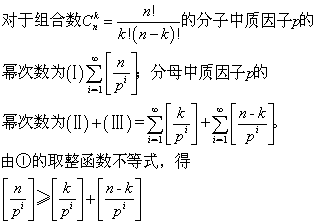
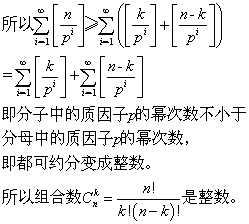
⑤卡特蘭數是整數
⑥卡特蘭數是整數的另一個證明
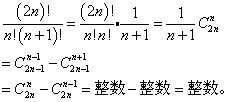
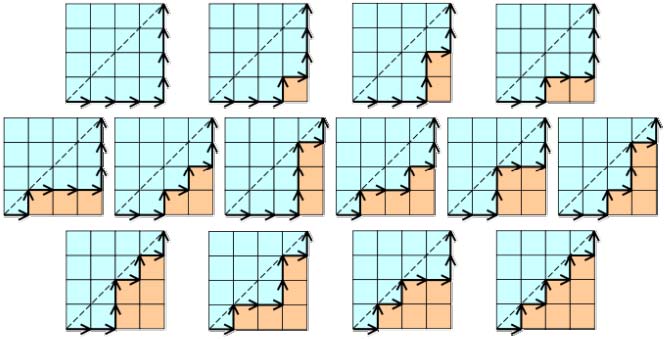
凸六邊形剖分成三角形的14種方法，是卡特蘭數C4
從左下角（0，0）走到右上角（4，4），只允許向上、向右走，但不允許穿過對角線的方法數是14種，是卡特蘭數C4
1936第40屆匈牙利奧林匹克數學競賽 第1題考了Catalan恒等式的證明。
1979第21屆國際數學奧林匹克 第1題考了一個卡特蘭恒等式的應用的題目
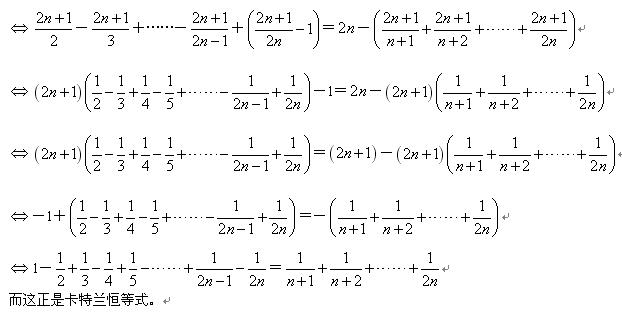
此題由1989年第1屆匈牙利-以色列數學競賽題改編。
轉自：
http://www.mathoe.com/dispbbs.asp?boardid=89&replyid=46004&id=34522&page=1&skin=0&Star=2