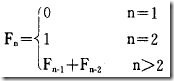斐�L那契�Q�Fabonacci�Q�序列�v源于中世�U�的意大利,问题是这��L��出的�Q�假�?strong>每对兔子每个月生出新的一对兔子来�Q?strong>新的每对兔子�q�两个月���可以生�?/strong>。其�ơ,�q�些兔子都不�?/strong>�Q�这��L��一个月有一对兔子,�W�二个月有两对兔子,�W�三个月有三对兔子(�W�一个月的一对兔子又生了一对)�Q�第四个月有五对兔子�Q�第二个月已有的两对兔子又各生了一对)�Q�以此类推,问一�q�共有多���对兔子�?/p> 可以把这个问题抽象一下:一般每个月的兔子数�?strong>上个月已有的兔子
于是乎得��C��所谓的斐�L那契序列�Q�它定义为:
���是��_��从第三项��h����w��是前两项的和�?/p>
在下面的���法里,把第一��看作了 0�Q�这样就更符合数学上�?#8220;斐�L那契”数列了:
1�Q���用递归�Ҏ���Q?/p>
int Fabonacci(int n) |
{ |
if(n <= 2) |
return n - 1; |
else |
return (Fabonacci(n - 1) + Fabonacci(n - 2)); |
} |
2�Q����?for 循环�Q�输��Z���?n 个斐波那契数列:
int _Fabonacci(int n)//输出�?n 个数 |
{ |
int i, a, b, c; |
a = 0; |
b = 1; |
printf("%10d%10d", a, b);/*输出前两个数*/ |
for(i = 3; i <= n; i ++) |
{ |
c = a + b; |
printf("%10d", c); |
if(i % 5 == 0) |
printf("\n");/*每行输出 5 �?/ |
a = b; |
b = c;/*��移�?/ |
} |
printf("\n"); |
}]]>
���单地说就是所有相�{�的数经�q�某�U�排序方法后�Q�仍能保持它们在排序之前的相�Ҏ��序,我们���p���q�种排序�Ҏ��是稳定的。反之,���是非稳定的。要注意�?
是,排序���法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中,只要有一个实例��得算法不满���E�_��性要求,则该排序���法���是不稳定的�?
比如�Q�一�l�数排序前是a1,a2,a3,a4,a5�Q�其中a2=a4�Q�经�q�某�U�排序后为a1,a2,a4,a3,a5�Q�则我们说这�U�排序是�E�_��的,因�ؓa2排序前在a4的前面,排序后它�q�是在a4的前面。假如变成a1,a4,a2,a3,a5��׃��是稳定的了�?/p>
2、内排序和外排序
在排序过�E�中�Q�所有需要排序的数都在内存,�q�在内存中调整它们的存储��序�Q�称为内排序�Q?br />在排序过�E�中�Q�只有部分数被调入内存,�q�借助内存调整数在外存中的存放��序排序�Ҏ���U�Cؓ外排序�?/p>
3、算法的旉���复杂度和�I�间复杂�?/p>
所谓算法的旉���复杂度,是指执行���法所需要的计算工作量�?br />一个算法的�I�间复杂度,一般是指执行这个算法所需要的内存�I�间�?/p>
=======================================
一.插入排序
首先新徏一个空列表�Q�用于保存已排序的有序数列(我们�U�C���?有序列表"�Q��?
从原数列中取��Z��个数�Q�将其插�?有序列表"中,使其仍旧保持有序状态�?
重复2��h��骤,直至原数列�ؓ�I��?
插入排序的��^均时间复杂度为��^方��的,效率不高�Q�但是容易实现。它借助�?逐步扩大成果"的思想�Q���有序列表的长度逐渐增加�Q�直臛_��长度�{�于原列表的长度�?/font>
①.直接插入排序(�E�_��)
接插入排序的�q�程为:在插入第i个记录时�Q�R1,R2,..Ri-1已经排好序,���第i个记录的排序码Ki依次和R1,R2,..,Ri-1的排序码逐个�q�行比较�Q�找到适当的位�|�。��用直接插入排序,对于��h��n个记录的文�g�Q�要�q�行n-1���排序�?br />
代码如下:
void Dir_Insert(int A[],int N) //直接插入排序
{
int j,t;
for(int i=1;i<N;i++)
{
t=A[i];
j=i-1;
while(A[j]>t)
{
A[j+1]=A[j];
j--;
}
A[j+1]=t;
}
}
②.希尔排序(不稳�?�Q?br />
希尔(Shell)排序的基本思想是:先取一个小于n的整数d1作�ؓ�W�一个增量把文�g的全部记录分成d1个组。所有距���Mؓd1的倍数的记录放在同一个组
中。先在各�l�内�q�行直接插入排序�Q�然后,取得�W�二个增量d2<d1重复上述的分�l�和排序�Q�直��x��取的增量di=1�Q�即所有记录放在同一�l�中�q�行直接
插入排序为止。该�Ҏ��实质上是一�U�分�l�插入方法�?br /> 一般取d1=n/2�Q�di+1=di/2。如果结果�ؓ偶数�Q�则�?�Q�保证di为奇数�?br /> 希尔排序是不�E�_��的,希尔排序的执行时间依赖于增量序列�Q�其�q�_��旉���复杂度�ؓO(n^1.3).
代码如下:
void Shell(int A[],int n) //Shell排序
{
int i,j,k,t;
(n/2)%2 == 0 ? k = n/2+1 : k = n/2; //保证增量为奇�?br /> while(k > 0)
{
for(j=k;j<n; j++)
{
t = A[j];
i = j - k;
while(i>=0 && A[i]>t)
{
A[i+k]=A[i];
i=i-k;
}
A[i+k]=t;
}
if(k == 1) break;
(k/2)%2 ==0 ? k=k/2+1 : k=k/2;
}
}
==============================================
�?选择排序
设数�l�内存放了n个待排数字,数组下标�?开始,到n�l�束�?
i=1
从数�l�的�W�i个元素开始到�W�n个元素,��L��最���的元素�?
���上一步找到的最���元素和�W�i位元素交换�?
如果i=n�Q?���法�l�束�Q�否则回到第3�?
①.直接选择排序(不稳�?
直接选择排序的过�E�是�Q�首先在所有记录中选出序码最���的记录�Q�把它与�W?个记录交换,然后在其余的记录内选出排序码最���的记录�Q�与�W?个记录交�?.....依次�c�L���Q�直到所有记录排完�ؓ止�?br />
无论文�g初始状态如何,在第i���排序中选出最���关键字的记录,需要做n-i�ơ比较,因此�Q��ȝ��比较�ơ数为n(n-1)/2=O(n^2)。当初始文�g为正
序时�Q�移动次��Cؓ0�Q�文件初态�ؓ反序�Ӟ��每趟排序均要执行交换操作�Q��ȝ���U�d���ơ数取最大�?(n-1)。直接选择排序的��^均时间复杂度为O(n^2)。直
接选择排序是不�E�_��的�?br />
代码如下:
void Dir_Choose(int A[],int n) //直接选择排序
{
int k,t;
for(int i=0;i<n-1;i++)
{
k=i;
for(int j=i+1;j<n;j++)
{
if(A[j]<A[k]) k=j;
}
if(k!=i)
{
t=A[i];
A[i]=A[k];
A[k]=t;
}
}
}
②.堆排�?不稳�?
�?
先新��Z��个空列表�Q�作用与插入排序中的"有序列表"相同�? 扑ֈ�数列中最大的数字�Q�将其加�?有序列表"的末���,�q�将其从原数列中删除�?
重复2��h��骤,直至原数列�ؓ�I��?
堆排序的�q�_��旉���复杂度�ؓnlogn,效率高(因�ؓ有堆�q�种数据�l�构以及它奇妙的特征�Q����?扑ֈ�数列中最大的数字"�q�样的操作只需要O(1)的时间复�?
度,�l�护需要logn的时间复杂度�Q�,但是实现相对复杂�Q�可以说是这�?�U�算法中比较隑֮�现的�Q��?
看�v来似乎堆排序与插入排序有些相像,但他们其实是本质不同的算法。至���,他们的时间复杂度差了一个数量���Q�一个是�q�x���U�的�Q�一个是�Ҏ���U�的�?
堆排序是一�U�树形选择排序�Q�是对直接选择排序的有效改�q�。n个关键字序列
K1,K2,...,Kn
�U�Cؓ堆,当且仅当该序列满��?Ki<=K2i且Ki<=K2i+1)�?Ki>=K2i且Ki>=K2i+1),(1&
lt;=i<=n/2)。根�l�点(堆顶)的关键字是堆里所有结点关键字中最���者,�U�Cؓ���根堆;根结点的关键字是堆里所有结点关键字中最大者,�U�Cؓ�?
根堆�?br /> 若将此序列所存储的向量R[1..n]看作是一���完全二叉树的存储结构,则堆实质上是满��如下性质的完全二叉树�Q�树中�Q一非叶�l�点的关键字均不大于(或不���于)其左叛_���?若存�?�l�点的关键字�?br />
堆排序的关键步骤有两个:一是如何徏立初始堆�Q�二是当堆的根结点与堆的最后一个结点交换后�Q�如何对���了一个结点后的结点序列做调整�Q���之重新成为堆。堆�?
序的最坏时间复杂度为O(nlog2n),堆排序的�q�_��性能较接�q�于最坏性能。由于徏初始堆所需的比�?
�ơ数较多�Q�所以堆排序不适宜于记录较���的文�g。堆排序是就地排序,辅助�I�间为O(1)�Q�它是不�E�_��的排序方法�?br />
代码�?.
====================================
�?交换排序
两两比较待排序记录的排序码,�q�交换不满����序要求的那写偶对,直到满��条�g为止。交换排序的主要�Ҏ��有冒泡排序和快速排�?
①.冒��排序(�E�_���?
�?
先将所有待排序的数字放入工作列表中�?从列表的�W�一个数字到倒数�W�二个数字,逐个���查:若某一位上的数字大于他的下一位,则将它与它的下一位交换�?
重复2��h��骤,直至再也不能交换�?冒��排序的��^均时间复杂度与插入排序相同,也是�q�x���U�的�Q�但也是非常�Ҏ��实现的算法�?nbsp;
冒��排序���被排序的记录数�l�R[1..n]垂直排列�Q�每个记录R[i]看作是重量�ؓki的气泡。根据轻气��不能在重气��之下的原则,从下往上扫描数�l�R�Q�凡扫描到违反本原则的轻气���Q�就使其向上"漂��Q"。如此反复进行,直到最后�Q何两个气泡都是轻者在上,重者在下�ؓ止�?br /> 冒��排序的具体过�E�如下:
�W�一步,先比较k1和k2�Q�若k1>k2�Q�则交换k1和k2所在的记录�Q�否则不交换。���l�对k2和k3重复上述�q�程�Q�直到处理完kn-1和kn。这时最大的排序码记录�{��C��最后位�|�,�U�第1�ơ�v泡,共执行n-1�ơ比较�?br /> 与第一步类��|��从k1和k2开始比较,到kn-2和kn-1为止�Q�共执行n-2�ơ比较�?br /> 依次�c�L���Q�共做n-1�ơ�v泡,完成整个排序�q�程�?br /> 若文件的初始状态是正序的,一���扫描即可完成排序。所需关键字比较次��Cؓn-1�ơ,记录�U�d���ơ数�?。因此,冒��排序最好的旉���复杂度�ؓO(n)�?br />
若初始文件是反序的,需要进行n-1���排序。每���排序要�q�行n-i�ơ关键字的比�?1<=i<=n-1),且每�ơ比较都必须�U�d��记录三次来达
��C��换记录位�|�。在�q�种情况下,比较�ơ数辑ֈ�最大值n(n-1)/2=O(n^2),�U�d���ơ数也达到最大�?n(n-1)/2=O(n^2)。因此,冒��
排序的最坏时间复杂度为O(n^2)�?br /> 虽然冒��排序不一定要�q�行n-1���,但由于它的记录移动次数较多,故��^均性能比直接插入排序要差得多。冒泡排序是���地排序�Q�且它是�E�_��的�?br />
代码如下:
void QP(int A[],int n) //优化的冒泡排�?
{
int count=0,t,flag;
for(int i=0;i<n-1;i++)
{
flag=0;
for(int j=0;j<n-i;j++)
{
if(A[j+1]<A[j])
{
t=A[j];
A[j]=A[j+1];
A[j+1]=t;
flag=1;
count+=3;
}
}
if(flag==0) break;
}
}
②.快速排序:(不稳定的)
实践�? 明,快速排序是所有排序算法中最高效的一�U�。它采用了分�ȝ��思想�Q�先保证列表的前半部分都���于后半部分�Q�然后分别对前半部分和后半部分排序,�q�样整个列表 ���有序了。这是一�U�先�q�的思想�Q�也是它高效的原因。因为在排序���法中,���法的高效与否与列表中数字间的比较次数有直接的关�p�,�?保证列表的前半部分都��? 于后半部�?��׃��得前半部分的��M��一个数从此以后都不再跟后半部分的数�q�行比较了,大大减少了数字间不必要的比较。但查找数据得另当别��Z���?
快速排序采用了一�U�分�ȝ���{�略�Q�通常�U�其为分��L���Q�其基本思想是:���原问题分解������q�个规模更小但结构与原问题相似的子问题。递归地解�q�些子问题,然后���这些子问题的解�l�合为原问题的解�?br /> 快速排序的具体�q�程如下�Q?br /> �W�一步,在待排序的n个记录中��d��一个记录,以该记录的排序码为准�Q�将所有记录分成两�l�,�W?�l�各记录的排序码都小于等于该排序码,�W?�l�各记录的排序码都大于该排序码,�q�把该记录排在这两组中间�?br /> �W�二步,采用同样的方法,对左边的�l�和双���的组�q�行排序�Q�直到所有记录都排到相应的位�|��ؓ止�?br />
代码如下:
void Quick_Sort(int A[],int low,int high) //low和high是数�l�的下标
{
if(low<high)
{
int temp,t=A[low];
int l=low,h=high;
while(l<h)
{
while(A[l]<t) l++;
while(A[h]>=t) h--;
if(h>l)
{
temp=A[l];
A[l]=A[h];
A[h]=temp;
}
}
Quick_Sort(A,low,l-1);
Quick_Sort(A,l+1,high);
}
}
==================================
�?归�ƈ排序
归�ƈ排序是将两个或两个以上的有序子表合�ƈ成一个新的有序表。初始时�Q�把含有n个结点的待排序序列看作由n个长度都�?的有序子表组成,���它们依�ơ两两归�q�得到长度�ؓ2的若�q�有序子表,再对它们两两合�ƈ。直到得到长度�ؓn的有序表�Q�排序结束�?br />
归�ƈ排序是一�U�稳定的排序�Q�可用顺序存储结构,也易于在链表上实玎ͼ�寚w��度�ؓn的文�Ӟ��需�q�行log2n���二路归�qӞ��每趟归�ƈ的时间�ؓO(n),故其旉���
复杂度无论是在最好情况下�q�是在最坏情况下均是O(nlog2n)。归�q�排序需要一个辅助向量来暂存两个有序子文件归�q�的�l�果�Q�故其辅助空间复杂度�?
O(n),昄���它不是就地排序�?br />
代码�?..
=================================
�?基数排序
讑֍�关键字的每个分量的取��D��围均是C0<=Kj<=Crd-1(0<=j<=rd),可能的取��g��数rd�U�Cؓ基数�Q�基数的选择和关键字的分解因关键字的�c�d��而异�Q?br /> (1).若关键字是十�q�制整数�Q�则按个、十�{�位�q�行分解�Q�基数rd=10,C0=0,C9=9,d为最长整数的位数�Q?br /> (2).若关键字是小写的英文字符�Ԍ��则rd=26,C0='a',C25='z',d为最长字�W�串的长度.
基数排序的基本思想是:从低位到高位依次对待排序的关键码�q�行分配和收集,�l�过d���分配和攉����Q�就可以得到一个有序序列.
===================================
�ȝ���ȝ���Q?/font>
按��^均时间将排序分�ؓ四类�Q?br />
�Q?�Q���^斚w��(O(n2))排序
一般称为简单排序,例如直接插入、直接选择和冒泡排序;
�Q?�Q�线性对数阶(O(nlgn))排序
如快速、堆和归�q�排序;
�Q?�Q�O(n1+�K?阶排�?br /> �K�是介于0�?之间的常敎ͼ��?<�K?lt;1�Q�如希尔排序�Q?br />�Q?�Q�线性阶(O(n))排序
如基数排序�?br />
各种排序�Ҏ��比较
���单排序中直接插入最好,快速排序最快,当文件�ؓ正序�Ӟ��直接插入和冒泡均最佟�?br />
影响排序效果的因�?/strong>
因�ؓ不同的排序方法适应不同的应用环境和要求�Q�所以选择合适的排序�Ҏ��应综合考虑下列因素�Q?br /> ①待排序的记录数目n�Q?br /> ②记录的大��?规模)�Q?br /> ③关键字的�l�构及其初始状态;
④对稳定性的要求�Q?br /> ⑤语言工具的条�Ӟ��
⑥存储�l�构�Q?br /> ⑦旉���和辅助空间复杂度�{��?br />
不同条�g下,排序�Ҏ��的选择
(1)若n较小(如n≤50)�Q�可采用直接插入或直接选择排序�?br /> 当记录规模较���时�Q�直接插入排序较好;否则因�ؓ直接选择�U�d��的记录数���于直接插�h�Q�应选直接选择排序为宜�?br />(2)若文件初始状态基本有�?指正�?�Q�则应选用直接插�h、冒泡或随机的快速排序�ؓ宜;
(3)若n较大�Q�则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序�?br />归�ƈ排序�?br /> 快速排序是目前��Z��比较的内部排序中被认为是最好的�Ҏ���Q�当待排序的关键字是随机分布�Ӟ��快速排序的�q�_��旉���最短;
堆排序所需的辅助空间少于快速排序,�q�且不会出现快速排序可能出现的最坏情��c��这两种排序都是不稳定的�?br />
若要求排序稳定,则可选用归�ƈ排序。但从单个记录�v�q�行两两归�ƈ�?nbsp;
排序���法�q�不值得提倡,通常可以���它和直接插入排序结合在一起��用。先利用直接插入排序求得较长的有序子文�g�Q�然后再两两归�ƈ之。因为直接插入排序是�E�_��
的,所以改�q�后的归�q�排序仍是稳定的�?/font>
=======================================
=========另一�?========================
=======================================
选择排序
在要排序的一�l�数中,选出最���的一个数与第一个位�|�的��C��换;
然后在剩下的数当中再找最���的与第二个位置的数交换�Q�如此��@�?br />到倒数�W�二个数和最后一个数比较为止�?
选择排序是不�E�_��的。算法复杂度O(n2)--[n的��^方]
void select_sort(int *x, int n)
{
int i, j, min, t;
for (i=0; i<n-1; i++) /*要选择的次敎ͼ�0~n-2共n-1��?/
{
min = i; /*假设当前下标为i的数最���,比较后再调整*/
for (j=i+1; j<n; j++)/*循环扑և�最���的数的下标是哪�?/
{
if (*(x+j) < *(x+min))
{
min = j; /*如果后面的数比前面的���,则记下它的下�?/
}
}
if (min != i) /*如果min在��@环中改变了,���需要交换数�?/
{
t = *(x+i);
*(x+i) = *(x+min);
*(x+min) = t;
}
}
}
直接插入排序
在要排序的一�l�数中,假设前面(n-1) [n>=2] 个数已经是排
好顺序的�Q�现在要把第n个数插到前面的有序数中,使得�q�n个数
也是排好��序的。如此反复��@环,直到全部排好��序�?br />
直接插入排序是稳定的。算法时间复杂度O(n2)--[n的��^方]
void insert_sort(int *x, int n)
{
int i, j, t;
for (i=1; i<n; i++) /*要选择的次敎ͼ�1~n-1共n-1��?/
{
/*
暂存下标为i的数。注意:下标�?开始,原因���是开始时
�W�一个数即下标�ؓ0的数�Q�前面没有�Q何数�Q�单单一个,认�ؓ
它是排好��序的�?br /> */
t=*(x+i);
for (j=i-1; j>=0 && t<*(x+j); j--) /*注意�Q�j=i-1�Q�j--�Q�这里就是下标�ؓi的数�Q�在它前面有序列中找插入位置�?/
{
*(x+j+1) = *(x+j); /*如果满��条�g���往后挪。最坏的情况���是t比下标�ؓ0的数都小�Q�它要放在最前面�Q�j==-1�Q�退出��@�?/
}
*(x+j+1) = t; /*扑ֈ�下标为i的数的放�|�位�|?/
}
}
冒��排序
在要排序的一�l�数中,对当前还未排好序的范围内的全部数�Q�自�?br />而下对相�ȝ��两个��C���ơ进行比较和调整�Q�让较大的数往下沉�Q�较
���的往上冒。即�Q�每当两盔R��的数比较后发现它们的排序与排序要
求相反时�Q�就���它们互换�?br />
下面是一�U�改�q�的冒�����法�Q�它记录了每一遍扫描后最后下沉数�?br />位置k�Q�这样可以减���外层��@环扫描的�ơ数�?/strong>
冒��排序是稳定的。算法时间复杂度O(n2)--[n的��^方]
void bubble_sort(int *x, int n)
{
int j, k, h, t;
for (h=n-1; h>0; h=k) /*循环到没有比较范�?/
{
for (j=0, k=0; j<h; j++) /*每次预置k=0�Q���@环扫描后更新k*/
{
if (*(x+j) > *(x+j+1)) /*大的攑֜�后面�Q�小的放到前�?/
{
t = *(x+j);
*(x+j) = *(x+j+1);
*(x+j+1) = t; /*完成交换*/
k = j; /*保存最后下沉的位置。这样k后面的都是排序排好了的�?/
}
}
}
}
希尔排序
在直接插入排序算法中�Q�每�ơ插入一个数�Q���有序序列只增�?个节点,
�q�且�Ҏ��入下一个数没有提供��M��帮助。如果比较相隔较�q�距���(�U�Cؓ
增量�Q�的敎ͼ�使得数移动时能跨�q�多个元素,则进行一�ơ比较就可能消除
多个元素交换。D.L.shell�?959�q�在以他名字命名的排序算法中实现
了这一思想。算法先���要排序的一�l�数按某个增量d分成若干�l�,每组�?br />记录的下标相差d.�Ҏ���l�中全部元素�q�行排序�Q�然后再用一个较���的增量
对它�q�行�Q�在每组中再�q�行排序。当增量减到1�Ӟ��整个要排序的数被分成
一�l�,排序完成�?br />
下面的函数是一个希���排序算法的一个实玎ͼ�初次取序列的一半�ؓ增量�Q?br />以后每次减半�Q�直到增量�ؓ1�?/strong>
希尔排序是不�E�_��的�?/strong>
void shell_sort(int *x, int n)
{
int h, j, k, t;
for (h=n/2; h>0; h=h/2) /*控制增量*/
{
for (j=h; j<n; j++) /*�q�个实际上就是上面的直接插入排序*/
{
t = *(x+j);
for (k=j-h; (k>=0 && t<*(x+k)); k-=h)
{
*(x+k+h) = *(x+k);
}
*(x+k+h) = t;
}
}
}
快速排�?/strong>
快速排序是对冒泡排序的一�U�本质改�q�。它的基本思想是通过一��?br />扫描后,使得排序序列的长度能大幅度地减少。在冒��排序中,一��?br />扫描只能���保最大数值的数移到正���位�|�,而待排序序列的长度可能只
减少1。快速排序通过一���扫描,���p�����保某个敎ͼ�以它为基准点吧)
的左边各数都比它���,双���各数都比它大。然后又用同��L���Ҏ��处理
它左右两边的敎ͼ�直到基准点的左右只有一个元素�ؓ止。它是由
C.A.R.Hoare�?962�q�提出的�?br />
昄���快速排序可以用递归实现�Q�当然也可以用栈化解递归实现。下面的
函数是用递归实现的,有兴���的朋友可以�Ҏ��非递归的�?/strong>
快速排序是不稳定的。最理想情况���法旉���复杂度O(nlog2n)�Q�最坏O(n2)
void quick_sort(int *x, int low, int high)
{
int i, j, t;
if (low < high) /*要排序的元素��h��下标�Q�保证小的放在左边,大的攑֜�双���。这里以下标为low的元素�ؓ基准�?/
{
i = low;
j = high;
t = *(x+low); /*暂存基准点的�?/
while (i<j) /*循环扫描*/
{
while (i<j && *(x+j)>t) /*在右边的只要比基准点大仍攑֜�双���*/
{
j--; /*前移一个位�|?/
}
if (i<j)
{
*(x+i) = *(x+j); /*上面的��@环退出:卛_��现比基准点小的数�Q�替换基准点的数*/
i++; /*后移一个位�|�,�q�以此�ؓ基准�?/
}
while (i<j && *(x+i)<=t) /*在左边的只要���于�{�于基准点仍攑֜�左边*/
{
i++; /*后移一个位�|?/
}
if (i<j)
{
*(x+j) = *(x+i); /*上面的��@环退出:卛_��现比基准点大的数�Q�放到右�?/
j--; /*前移一个位�|?/
}
}
*(x+i) = t; /*一遍扫描完后,攑ֈ�适当位置*/
quick_sort(x,low,i-1); /*对基准点左边的数再执行快速排�?/
quick_sort(x,i+1,high); /*对基准点双���的数再执行快速排�?/
}
}
堆排�?/strong>
堆排序是一�U�树形选择排序�Q�是对直接选择排序的有效改�q��?br />堆的定义如下�Q�具有n个元素的序列�Q�h1,h2,...,hn),当且仅当
满���Q�hi>=h2i,hi>=2i+1�Q�或�Q�hi<=h2i,hi<=2i+1�Q?i=1,2,...,n/2)
时称之�ؓ堆。在�q�里只讨论满���_��者条件的堆�?/strong>
由堆的定义可以看出,堆顶元素�Q�即�W�一个元素)必�ؓ最大项。完全二叉树可以
很直观地表示堆的�l�构。堆���ؓ根,其它为左子树、右子树�?br />初始时把要排序的数的序列看作是一���顺序存储的二叉树,调整它们的存储顺序,
使之成�ؓ一个堆�Q�这时堆的根节点的数最大。然后将根节点与堆的最后一个节�?br />交换。然后对前面(n-1)个数重新调整使之成�ؓ堆。依此类推,直到只有两个节点
的堆�Q��ƈ对它们作交换�Q�最后得到有n个节点的有序序列�?/strong>
从算法描�q�来看,堆排序需要两个过�E�,一是徏立堆�Q�二是堆��与堆的最后一个元�?br />交换位置。所以堆排序有两个函数组成。一是徏堆的渗透函敎ͼ�二是反复调用渗透函�?br />实现排序的函数�?/strong>
堆排序是不稳定的。算法时间复杂度O(nlog2n)�?/strong>
渗透徏�?/strong>
void sift(int *x, int n, int s)
{
int t, k, j;
t = *(x+s); /*暂存开始元�?/
k = s; /*开始元素下�?/
j = 2*k + 1; /*叛_��树元素下�?/
while (j<n)
{
if (j<n-1 && *(x+j) < *(x+j+1))/*判断是否满��堆的条�g�Q�满���_���l�箋下一轮比较,否则调整�?/
{
j++;
}
if (t<*(x+j)) /*调整*/
{
*(x+k) = *(x+j);
k = j; /*调整后,开始元素也随之调整*/
j = 2*k + 1;
}
else /*没有需要调整了�Q�已�l�是个堆了,退出��@环�?/
{
break;
}
}
*(x+k) = t; /*开始元素放到它正确位置*/
}
堆排�?/strong>
void heap_sort(int *x, int n)
{
int i, k, t;
int *p;
for (i=n/2-1; i>=0; i--)
{
sift(x,n,i); /*初始建堆*/
}
for (k=n-1; k>=1; k--)
{
t = *(x+0); /*堆顶攑ֈ�最�?/
*(x+0) = *(x+k);
*(x+k) = t;
sift(x,k,0); /*剩下的数再徏�?/
}
}
===============================================================================
void main()
{
#define MAX 4
int *p, i, a[MAX];
/*录入���试数据*/
p = a;
printf("Input %d number for sorting :\n",MAX);
for (i=0; i<MAX; i++)
{
scanf("%d",p++);
}
printf("\n");
/*���试选择排序*/
p = a;
select_sort(p,MAX);
/**/
/*���试直接插入排序*/
/*
p = a;
insert_sort(p,MAX);
*/
/*���试冒��排序*/
/*
p = a;
insert_sort(p,MAX);
*/
/*���试快速排�?/
/*
p = a;
quick_sort(p,0,MAX-1);
*/
/*���试堆排�?/
/*
p = a;
heap_sort(p,MAX);
*/
for (p=a, i=0; i<MAX; i++)
{
printf("%d ",*p++);
}
printf("\n");
system("pause");
]]>