sdfond 2010-04-26 23:34 ÕÅæĶĪ©Ķ»äĶ«║
]]>ŃĆĆŃĆĆĶ«Šd1 = gcd(a, b), d2 = gcd(b, a % b), a > bõĖöa = qb + r
ŃĆĆŃĆĆÕŬķ£ĆĶ»üd1 | d2“qČõĖöd2 | d1ŃĆ?br>ŃĆĆŃĆĆÕøĀõžōd2 | b, d2 | r, ÕøĀµŁżd2 | (b + qr) = aÕQīµĀ╣µŹ«d2 | bõĖöd2 | aµ£ēd2 | gcd(a, b)ÕQīÕŹ│d2 | d1ŃĆ?br>ŃĆĆŃĆĆÕøĀõžōd1 | a, d1 | b, ÕøĀµŁżd1 | (a - qb) = rÕQīµĀ╣µŹ«d1 | bõĖöd1 | rµ£ēd1 | gcd(b, r)ÕQīÕŹ│d1 | d2ŃĆ?br>ŃĆĆŃĆƵĀęÄŹ«EuclidĮÄŚµ│Ģµē¦ĶĪīśqćń©ŗÕQīgcd(a, b) = gcd(b, r) = gcd(r, b % r) = ... = gcd(rn, rn-1 % rn)ÕQīÕ”éµ×£rn-1 % rn = 0ÕQīµĀ╣µŹ«gcd(a, 0) = aÕQīµ£ēgcd(a, b) = rnÕQīĶ»üµ»ĢŃĆ?br>
ŃĆĆŃĆĆĶ▓īõ╝╝ÕüÅÕ║ÅÕģ│ń│╗õĖŖĶ»üa = bÕŠłÕżÜķāĮµś»Õł®ńö©ÕÅŹÕ»╣┐U░µĆ¦’╝īµ»öÕ”éa >= b“qČõĖöb >= aÕłÖa = bÕQīµł¢ĶĆģa | b“qČõĖöb | aÕłÖa = bÕQīõĖĆõĖ¬ÕŠłÕĖĖńö©õĖöÕ╝║Õż¦ńÜäµ¢ęÄ│ĢŃĆ?br>
sdfond 2010-04-24 21:29 ÕÅæĶĪ©Ķ»äĶ«║
]]>ŃĆÉķóśńø«Õłåµ×ÉŃĆ?br>ŃĆĆŃĆĆśqÖµś»õĖĆķüōBTķóś’╝īõĖŁķŚ┤Ķ«äĪĮ«õ║åĶ«ĖÕżÜtrickŃĆéÕ╝ĆÕ¦ŗÕ»╣ķóśµäŵ▓Īµ£ēÕ«īÕģ©ńÉåĶ¦ŻÕQīķöÖõ║åÕŠłÕżÜµ¼ĪÕQīÕÉÄµØźµēŠµØźõ║åµĢ░µŹ«ÕQīµēŹÕÅæńÄ░õ║åķŚ«ķóśŃĆ?br>ŃĆĆŃĆĆķóśńø«õĖŁµÅÅśq░ńÜäĶÄ»éā£Į{¢ńĢźµś»’╝Ü"A player wins if after his move the size of some heap is a prime number."śqÖÕÅźĶ»Øõ╣ŹõĖĆń£ŗõ╗źõĖ║µś»ÕÅ¢Õ«īń¤ø_ŁÉÕÉÄÕē®õĖŗńÜäń¤ø_ŁÉõĖ¬µĢ░µś»ń┤ĀµĢ░ńÜ䵌ČÕĆÖÕ░▒ĶÄ»éā£ÕQīÕģČÕ«×Ķ┐śķÜÉĶŚÅńØĆÕÅ”õĖĆ┐UŹÕÅ»ĶāĮ’╝ÜÕ”éµ×£ÕżÜÕĀåń¤ø_ŁÉõĖ¬µĢ░µś»ń┤ĀµĢÄ═╝īÕĮōÕēŹńÄ®Õ«ČµŚĀĶ«║µĆĵĀĘÕÅ¢ķāĮĶāĮĶÄĘĶā£’╝īÕøĀõžōÕ£©õ╗¢ÕÅ¢Õ«īõ╣ŗÕÉÄÕQīÕģČõ╗¢ÕĀåńÜäń¤│ÕŁÉõĖ¬µĢ░µś»ń┤ĀµĢ░ÕQīõ╣¤µ╗ĪĶā÷ĶÄ»éā£µØĪõÜgŃĆ?br>ŃĆĆŃĆƵğõĖŗµØźĶĆāĶÖæõĖĆĶł¼µāģÕå³cĆéĶ┐ÖõĖ¬ķóśńø«µś»ķÖÉÕłČõĖŁķŚ┤ńŖȵĆüńÜäNimµĖĖµłÅÕQīõ╣¤×«▒µś»Ķ»▀_╝īÕ»╣õ║ÄõĖĆÕĀåõĖ¬µĢŅCžōnńÜäń¤│ÕŁÉĶĆīĶ©ĆÕQīÕ«āńÜäSGÕĆ╝ÕÅ¢Õå│õ║Ä׫Åõ║ÄnńÜäµ£ĆÕż¦ń┤ĀµĢ░ŃĆéµ│©µäÅĶ┐ÖķćīķóśĶ«æųÅłµ£ēõ║åõĖĆõĖ¬Õ░ÅtrickÕQīķóśńø«Ķ»┤µśÄõ║åķ£ĆĶ”üÕÅ¢1Õł░kõĖ¬’╝īÕ”éµ×£ÕĮōÕēŹń¤ø_ŁÉõĖ¬µĢ░µ£¼ĶĒnµś»ń┤ĀµĢÄ═╝īÕĮōńäȵś»µ▓Īńö©ńÜäÕQīÕøĀµŁżµś»×«Åõ║ÄnńÜäµ£ĆÕż¦ń┤ĀµĢ░ŃĆéĶ«Š×«Åõ║ÄnńÜäµ£ĆÕż¦ń┤ĀµĢ░µś»p(ķóśńø«õĖŁĶ»┤µśÄõ║åń¤ø_ŁÉõĖ¬µĢ░Õż¦õ║Ä2ÕQīÕøĀµŁżpõĖĆÕ«ÜÕŁśÕ£?ÕQīķéŻõ╣łÕÅ»õ╗źÕ£©kµŁźõ╗źÕåģÕł░ĶŠŠpńÜäõĖĆիܵś»Õ┐ģĶā£µĆü’╝īĶĆīõĖöµś»ńø┤µÄźĶÄĘĶā£’╝īķ£ĆĶ”üÕ£©ĶŠōÕģźńÜ䵌ČÕĆÖńē╣Õł?śqÖõĖĆńéÜw£ĆĶ”üµ│©µäÅ’╝īÕ£©Ķ¦ŻÕå│ķÖÉÕłČõĖŁķŚ┤ńŖȵĆüńÜäNimµĖĖµłÅµŚČõĖĆĶł¼ķāĮķ£ĆĶ”üńē╣Õł?ŃĆéńäČÕÉÄÕ░▒µś»p + k + 1śqÖõĖ¬ńŖȵĆü’╝īÕøĀõžōÕ«āÕÅ»ĶŠäĪÜäńŖȵĆüÕģ©µś»Õ┐ģĶā£µĆü’╝īÕøĀµŁżÕ«āµś»Õ┐ģĶė|µĆü’╝īSGÕĆķgžō0ŃĆéńÄ░Õ£©ĶĆāĶÖæÕż¦õ║Äp + k + 1ńÜäńŖȵĆü’╝īķŚ«ķóśÕć║µØźõ║åŃĆéõ╗źp + k + 2śqÖõĖ¬ńŖȵĆüõžōõŠŗ’╝īÕøĀõžōÕ«āÕÅ»õ╗źÕł░ĶŠŠp + 2 ... p + k + 1śqÖõ║øńŖȵĆü’╝īÕøĀõžōp + 2 ... p + kķāĮµś»ńø┤µÄźĶÄ»éā£ńŖȵĆü’╝īÕ”éõĮĢÕłżÕ«Üõ╗¢õ╗¼ńÜäSGÕĆ╝ÕæóÕQ¤Õ”éµ×£ÕüćĶ«æų«āõ╗¼ńÜäSGÕĆ╝µś»1ÕQīķéŻõ╣łp + k + 2śqÖõĖ¬ńŖȵĆüńÜäSGÕĆ╝Õ║öĶ»źµś»2ŃĆéõĮåµś»µĆØĶĆāõĖĆõĖŗSGÕĆ╝ńÜäÕ«Üõ╣ēÕQīÕ«āµś»Õ«Üõ╣ēÕ£©õĖĆõĖ¬DAGõĖŖńÜäÕQīµēƵ£ēńÜäńŖȵĆüµ£ĆÕÉÄķāĮµś»ÕÅ»õ╗źÕ£©µ£ēķÖɵŁźÕåģĶĮ¼ń¦╗Õł░ń╗łµŁóµĆ?Õ┐ģĶė|µĆ?ŃĆéõĮåµś»p + 1 ... p + kśqÖõ║øńŖȵĆüķāĮĶĮ¼ń¦╗ÕłŅC║åpśqÖõĖ¬ńŖȵĆüõĖŖÕQīµłæõ╗¼Ķé»Õ«ÜõĖŹĶāĮĶ«żÕ«ÜpńŖȵĆüµś»ŠlłµŁóµĆü’╝īÕøĀµŁżõ╗ģõ╗ģÕćŁÕƤp + 1 ... p + kśqÖõ║øńŖȵĆüµś»Õ┐ģĶā£µĆüÕ░▒ĮÄĆÕŹĢńÜäµŖŖÕ«āõ╗¼ńÜäSGÕĆŲD«ŠõĖ?µś»õĖŹµü░ÕĮōńÜä’╝øśqÖõ║øķÖÉÕłČńŖȵĆüÕÆīõ╗źÕēŹńÜäķóśńø«Ķ┐śõĖŹÕÉīÕQīĶ┐Öõ║øķÖÉÕłČńŖȵĆüķāĮõĖŹĶāĮĶĮ¼ń¦╗Õł░ń╗łµŁóµĆüõĖŖÕQīõĮåµś»ńö▒õ║Äķóśńø«ńÜäĶ”üµ▒éÕQīÕ«āõ╗¼ÕÅłķāĮµś»Õ┐ģĶā£µĆü’╝īÕøĀµŁżµŖŖÕ«āõ╗¼ńÜäSGÕĆŲD«ŠõĖ║µŚĀĮIĘÕż¦µø┤ÕÉłķĆéõ║øŃĆ?br>ŃĆĆŃĆĆõ╗öń╗åµĆØĶĆāõĖĆõĖŗÕĖ”ķÖÉÕłČńŖȵĆüńÜäSGµĖĖµłÅÕQīÕÅ»õ╗źÕÅæńÄÄ═╝īÕ«āõ╗¼ÕÆīõĖĆĶł¼ńÜäSGµĖĖµłÅńÜäÕī║Õł½Õ£©õ║Ä’╝īÕ£©Õłåµ×ÉõĖĆĶł¼ńÜäSGµĖĖµłÅńÜ䵌ČÕĆÖ’╝īÕ»╣õ║ÄõĖĆõĖ¬ńŖȵĆüÕøŠĶĆīĶ©ĆÕQīĶØ{┐Ušdł░ŠlłµŁóµĆüńÜ䵌ČÕĆÖÕŲłõĖŹµäÅÕæ│ńØƵĖĖµłÅŠlōµØ¤ÕQīÕøĀõĖ║ńĮիČÕÅ»õ╗źķĆÜĶ┐ćĶĄ░ÕģČõ╗¢ńÜäńŖȵĆüÕøŠµØźõ┐ØĶ»üµś»ÕÉ”ĶŠŠÕł░Õ┐ģĶā£µĆü’╝øõĮåµś»ÕĖ”ķÖÉÕłČńŖȵĆüńÜäSGµĖĖµłÅÕQīķÖÉÕłČńÜäńŖȵĆüÕÅīµ¢ÜwāĮµś»õĖŹµĢóĶĄ░ńÜä’╝īÕøĀõžōõĖƵŚ”õĖƵ¢╣ĶĄ░ÕģźķÖÉÕłČńŖȵĆü’╝īÕÅ”õĖƵ¢╣ń½ŗÕł╗ĶÄĘĶā£’╝īµĖĖµłÅ׫▐q╗łµŁóõ║åŃĆéÕÅ»õ╗źĶ«żõĖ║’╝īÕŬĶ”üĶĄ░ÕģźķÖÉÕłČµĆüÕ░▒ńøĖÕĮōõ║ÄĶ«żĶŠō’╝īÕ»╣õ║ÄÕÅīµ¢╣ńĮիČĶĆīĶ©ĆĶé»Õ«ÜķāĮõĖŹõ╝ÜĶ┐ÖµĀĘÕüÜÕQīÕøĀµŁżĶ┐Öõ║øķÖÉÕłČńŖȵĆüÕ░▒µłÉõ║哵Ł╚ØŖȵĆ?#8221;ÕQīÕ«īÕģ©ÕÅ»õ╗źÕ┐ĮĶ¦åĶ┐Öõ║øńŖȵĆü’╝łõ╣¤Õ░▒µś»Ķ»┤õĖŹÕŁśÕ£©Õł░śqÖõ║øńŖȵĆüńÜäĶĮ¼ń¦╗ÕQēŃĆéķĆÜĶ┐ćõĖŖĶ┐░Õłåµ×ÉÕQīµłæõ╗¼ÕÅ»õ╗źĶ«żÕ«Üp + k + 2śqÖõĖ¬ńŖȵĆüńÜäSGÕĆ╝Õ║öĶ»źµś»1ĶĆīõĖŹµś?ŃĆ?br>ŃĆĆŃĆĆńÄ░Õ£©śqÖõĖ¬ķŚ«ķóśńÜäÕüܵ│ĢÕ░▒µ»öĶŠāµśÄµ£Śõ║å’╝īÕ»╣õ║ĵ»ÅÕĀåń¤ø_ŁÉÕQīÕÄ╗µÄēķÖÉÕłČµĆüńÜäĶ«©Ķ«║ÕÉÄ’╝ī׫▒ÕÅśµłÉõ║åÕ£©ķøåÕÉł{1...k}õĖŁķĆēµŗ®Õģāń┤ĀńÜäõĖĆõĖ¬Subtraction GameÕQīÕ«āńÜäSGÕĆ╝µś»µ©?k + 1)ÕŠ¬ńÄ»ńÜäŃĆ?br>ŃĆĆŃĆĆńäČÕÉÄ׫▒µś»µ▒éµ£Ćśqæń┤ĀµĢ░ńÜäķŚ«ķóśõ║å’╝īśqÖõĖ¬µ▓Īµ£ēÕźĮÕŖ×µ│Ģ’╝īÕŬĶāĮµÜ┤ÕŖøµ×ÜõŗDŃĆéÕ»╣õ║ÄõĖĆõĖ¬µĢ░nÕQīÕ£©sqrt(n)Õł░nõ╣ŗķŚ┤ÕŁśÕ£©ń┤ĀµĢ░ÕQłµä¤Ķ¦ēÕ║öĶ»źµś»ÕQīõĮåµś»õĖŹõ╝ÜĶ»üÕQē’╝īÕøĀµŁżµ£ĆÕżÜµ×ÜõĖŠsqrt(n)ŗŲĪÕ░▒ĶāĮµēŠÕł░Ķ¦ŻŃĆéõĮåµś»µ»ÅŗŲĪµ×ÜõĖæųłżń┤ĀńÜäÕżŹµØéÕ║”Ķ┐śµś»sqrt(n)ÕQīµĆšdżŹµØéÕ║”śqśµś»µ»öĶŠāķ½ś’╝īµłæÕ£©µ£¼Õ£░ĶĘæµĢ░µŹ«ĶĘæõ║?┐UÆ’╝īõ║żõĖŖÕÄ╗ĶČģµŚČõ║åÕQłSPOJńÜ䵌ČķÖ?0┐UÆ’╝īśqÖÕ▒ģńäČõ╣¤ŁæģµŚČÕQīµĢ░µŹ«Õż¤ÕÅśµĆü’╝ēŃĆéµā│õ║åÕŠłõ╣ģõ╣¤µ▓Īµ£ēõ╗Ćõ╣łµ¢░ńÜäń«Śµ│Ģ’╝īµŚĀÕźłÕŬĶāĮÕ£©Õłżń┤ĀõĖŖõĖŗńé╣ÕŖ¤Õż½ÕQīńø┤µÄźµŖŖMiller-RabinµÉ×Õć║µØźõ║åÕQīķƤÕ║”µÅÉķ½śÕłŅC║å2┐UÆ’╝īõ╗ŹńäČŁæģµŚČŃĆéÕÉÄµØźÕÅłÕŖĀõ║åõĖĆõ║øÕĖĖµĢŅCĖŖńÜäõ╝śÕī¢’╝īŠlłõ║Äśqćõ║åŃĆ?br>
ŃĆɵĆ╚Ø╗ōŃĆ?br>ŃĆĆŃĆĆśqÖõĖ¬ķóśńø«ÕüÜõ║åÕŠłķĢ┐µŚēÖŚ┤ÕQīõĖƵ¢ÜwØóµś»Õ«ĪķóśõĖŹµĖģ’╝īķöÖõ║åÕćĀµ¼ĪÕQøÕÅ”õĖƵ¢ÜwØóµś»Õ»╣õ║ÄSGńÜäńÉåĶ«║ńÉåĶ¦ŻńÜäõĖŹÕż¤ķĆÅÕĮ╗ÕQīµā│õ║åÕŠłõ╣ģń╗łõ║ĵā│µśÄńÖĮõ║å’╝øÕåŹµ£ē׫▒µś»õ╝śÕī¢ĮÄŚµ│Ģõ╣¤ĶŖ▒õ║åÕŠłķĢ┐µŚČķŚ┤ŃĆéõĖŹśqćķĆÜĶ┐ćśqÖõĖ¬ķóśńø«Õ»╣õ║ÄSGńÉåĶ«║ńÜäńÉåĶ¦ŻÕÅłśqøõ║åõĖƵŁź’╝īµä¤Ķ¦ēõĖŹķöÖÕQīÕæĄÕæ³cĆ?
µ│©’╝ܵ£¼µ¢ćõĮ£õ║Ä2009“q?µ£?µŚ?9ńé?7Õł?br>
sdfond 2010-02-06 09:04 ÕÅæĶĪ©Ķ»äĶ«║
]]>ŃĆÉķóśńø«Õłåµ×ÉŃĆ?br>ŃĆĆŃĆĆśqÖõĖ¬ķóśńø«õ╣ŹõĖĆń£ŗµī║ĮÄĆÕŹĢńÜäÕQīõĮåµś»µā│ÕüÜÕ»╣śqśµś»Ķ”üõ╗öŠlåńÜäµĆØĶĆāõĖŗńÜäŃĆéĶĪźķøåĶØ{Õī¢ńÜäµĆصā│ÕQīµ▒éÕć║µēƵ£ēÕģ▒ŠU┐ńÜäõĖēÕģāŠlä’╝īńäČÕÉÄńö©µĆ└LĢ░ÕćŵÄē׫▒µś»Į{öµĪłõ║å’╝īÕģ│ķö«×«▒µś»Õ”éõĮĢµ▒éÕģ▒ŠU┐õĖēÕģāń╗äŃĆéxÕØɵĀćńøĖÕÉīÕÆīyÕØɵĀćńøĖÕÉīńÜäµ»öĶŠāÕźĮĶ«Īń«ŚÕQīÕ£©õĖƵØĪµ¢£ŠU┐ńÜä׫ūāĖŹÕźĮń«Śõ║å’╝īńöųMĖ¬ÕøæųÅæńÄÄ═╝īÕŹ│õŗ╔µ¢£ńÄćńøĖÕÉīńÜäń║┐ÕQīń╗ÅśqćńÜäµĀ╝ńé╣µĢ░ÕÅ»ĶāĮÕÉäõĖŹńøĖÕÉīŃĆéµĆØĶĄ\ÕĮōńäČśqśµś»µ×ÜõŗDy / xÕQłõĖŹÕÉīńÜäy / x╝ŗ«Õ«Üõ║åõĖŹÕÉīńÜäń¤®Õ┼×Õī║Õ¤¤ÕQē’╝īõ╣ŗÕÉÄÕ”éõĮĢµ£ēµĢłńÜäĶ«ĪĮÄŚ’╝īµłæķććńö©ńÜäµ¢ęÄ│ĢÕÅ»ĶāĮµ£ēõ║øķ║╚Øā”ÕQīµ£ēńé╣ń▒╗Õ«ęÄ¢źńÜäµ¢╣µ│ĢŃĆéõ╗źµ¢£ńÄćõĖ║a / bõĖ▐ZŠŗÕQ?a, b) = gÕQīķéŻõ╣łm * nńÜäÕī║Õ¤¤ÕåģõĖĆիܵ£ē(m - a + 1) * (n - b + 1)õĖ¬ķéŻõ╣łÕż¦ńÜäń¤®ÕĮó’╝īśqÖµĀĘńÜäń¤®ÕĮóń╗ÅśqćńÜäµĀ╝ńé╣µĢ░µś»(g + 1)ÕQøńäČÕÉÄÕøĀõĖ║ÕÉīĮ{ēµ¢£ńÄćÕ░ÅõĖĆńé╣ńÜäń¤®Õ┼×(a - a / g, b - b / g)õ╣¤µś»ÕŁśÕ£©ńÜä’╝īõĖ¬µĢ░ÕÉīµĀĘÕÅ»õ╗źŠl¤Ķ«ĪÕć║µØźÕQīõĮåµś»µ£ēõ║øÕż¦ń¤®Õ┼×Õīģµŗ¼õ║å’╝īĶ”üÕÄ╗µÄē’╝øÕøĀµŁż×«▒ķććńö©Ķ┐Ö┐UŹµĆصā│ÕQīÕģłµ▒éÕć║Õż¦ń¤®ÕĮóńÜäõĖ¬µĢ░ÕQīńäČÕÉÄõŠØŗŲĪÕŠĆõĖŗÕćÅÕQīÕ░▒ÕÅ»õ╗źķü┐ÕģŹķćŹÕżŹĶ«ĪµĢ░õ║åŃĆéĶÖĮńäČĶ┐ÖµĀĘÕżŹµØéÕ║”µ£ēńé╣ķ½ś’╝īõĖŹĶ┐ćµ×üķÖɵĢ░µŹ«śqśµś»µ»öĶŠāÕ┐½ńÜäĶĘæÕć║µØźõ║åŃĆ?br>ŃĆĆŃĆĆĶ»┤ńÜäÕÅ»ĶāĮõĖŹÕż¬µĖģµźÜÕQīÕģĘõĮōõ╗ŻńĀüÕ”éõĖŗ’╝Ü
1 #include <cstdio>
2 #include <iostream>
3 using namespace std;
4 const int N = 1024;
5
6 bool tag[N][N];
7 long long calc(long long n)
8 {
9 if (n <= 2)
10 return 0;
11 return n * (n - 1) * (n - 2) / 6;
12 }
13 int gcd(int a, int b)
14 {
15 return b == 0 ? a : gcd(b, a % b);
16 }
17
18 int main()
19 {
20 int m, n, g, a, b, timer = 1, cnt[N], ta, tb;
21 long long ans;
22
23 while (scanf("%d %d", &m, &n) == 2)
24 {
25 memset(tag, 0, sizeof(tag));
26 if (m == 0 && n == 0)
27 break;
28 ans = calc((m + 1) * (n + 1)) - calc(m + 1) * (n + 1) - calc(n + 1) * (m + 1);
29 for (int i = m; i >= 1; i--)
30 for (int j = n; j >= 1; j--)
31 {
32 g = gcd(i, j);
33 a = i / g, b = j / g;
34 if (tag[a][b]) continue;
35 memset(cnt, 0, sizeof(cnt));
36 tag[a][b] = 1;
37 a = i, b = j;
38 ta = i / g, tb = j / g;
39 for (int k = g; k >= 2; k--)
40 {
41 cnt[k] += (m - a + 1) * (n - b + 1);
42 ans -= calc(k + 1) * cnt[k] * 2;
43 for (int t = 1; t <= k - 2; t++)
44 cnt[k-t] -= (t + 1) * cnt[k];
45 a -= ta, b -= tb;
46 }
47 }
48 cout << "Case " << timer++ << ": " << ans << endl;
49 }
50
51 return 0;
52 }
53
2 #include <iostream>
3 using namespace std;
4 const int N = 1024;
5
6 bool tag[N][N];
7 long long calc(long long n)
8 {
9 if (n <= 2)
10 return 0;
11 return n * (n - 1) * (n - 2) / 6;
12 }
13 int gcd(int a, int b)
14 {
15 return b == 0 ? a : gcd(b, a % b);
16 }
17
18 int main()
19 {
20 int m, n, g, a, b, timer = 1, cnt[N], ta, tb;
21 long long ans;
22
23 while (scanf("%d %d", &m, &n) == 2)
24 {
25 memset(tag, 0, sizeof(tag));
26 if (m == 0 && n == 0)
27 break;
28 ans = calc((m + 1) * (n + 1)) - calc(m + 1) * (n + 1) - calc(n + 1) * (m + 1);
29 for (int i = m; i >= 1; i--)
30 for (int j = n; j >= 1; j--)
31 {
32 g = gcd(i, j);
33 a = i / g, b = j / g;
34 if (tag[a][b]) continue;
35 memset(cnt, 0, sizeof(cnt));
36 tag[a][b] = 1;
37 a = i, b = j;
38 ta = i / g, tb = j / g;
39 for (int k = g; k >= 2; k--)
40 {
41 cnt[k] += (m - a + 1) * (n - b + 1);
42 ans -= calc(k + 1) * cnt[k] * 2;
43 for (int t = 1; t <= k - 2; t++)
44 cnt[k-t] -= (t + 1) * cnt[k];
45 a -= ta, b -= tb;
46 }
47 }
48 cout << "Case " << timer++ << ": " << ans << endl;
49 }
50
51 return 0;
52 }
53
sdfond 2009-10-15 19:54 ÕÅæĶĪ©Ķ»äĶ«║
]]> #include <cstdio>
#include <cstdio> #include <cmath>
#include <cmath> #include <algorithm>
#include <algorithm> using namespace std;
using namespace std; const int MOD = 11, N = 100001;
const int MOD = 11, N = 100001;
 int d[N], m[N];
int d[N], m[N]; int power_mod(int a, int b)
int power_mod(int a, int b) {
{ int ret = 1, f = a;
int ret = 1, f = a; while (b)
while (b) {
{ if (b & 1)
if (b & 1) ret = ret * f % MOD;
ret = ret * f % MOD; f = f * f % MOD;
f = f * f % MOD; b >>= 1;
b >>= 1; }
} return ret;
return ret; }
} void init()
void init() {
{ int tmp;
int tmp; for (int i = 2; i < N; i++)
for (int i = 2; i < N; i++) {
{ tmp = (int)(ceil(i * log(i) / log(10.0) + 1e-2) + 1e-1);
tmp = (int)(ceil(i * log(i) / log(10.0) + 1e-2) + 1e-1); d[i] = tmp;
d[i] = tmp; m[i] = power_mod(i % MOD, i);
m[i] = power_mod(i % MOD, i); }
} }
}
 int main()
int main() {
{ char str[N*5];
char str[N*5]; int T, p, len, tmp;
int T, p, len, tmp;
 init();
init(); scanf("%d", &T);
scanf("%d", &T); while (T--)
while (T--) {
{ scanf("%s", str);
scanf("%s", str); len = strlen(str);
len = strlen(str); if (len == 1 && str[0] == '1')
if (len == 1 && str[0] == '1') {
{ puts("1");
puts("1"); continue;
continue; }
} p = lower_bound(d, d + N, len) - d;
p = lower_bound(d, d + N, len) - d; tmp = 0;
tmp = 0; for (int i = 0; i < len; i++)
for (int i = 0; i < len; i++) {
{ tmp = tmp * 10 + (str[i] - '0');
tmp = tmp * 10 + (str[i] - '0'); tmp = tmp % MOD;
tmp = tmp % MOD; }
} printf("%d\n", tmp == m[p] ? p : -1);
printf("%d\n", tmp == m[p] ? p : -1); }
}
 return 0;
return 0; }
}
sdfond 2009-06-12 11:15 ÕÅæĶĪ©Ķ»äĶ«║
]]>sdfond 2009-06-10 09:16 ÕÅæĶĪ©Ķ»äĶ«║
]]>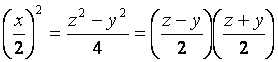
ŃĆĆŃĆĆõ╗żu = (z - y) / 2ÕQīv = (z + y) / 2ŃĆéÕøĀõĖ║yŃĆüzõ║ÆĶ┤©ÕQīķéŻõ╣łuŃĆüvõ║ÆĶ┤©ŃĆéÕ”éµ×£õĖŹõ║ÆĶ┤©ÕQīµ£ēv = kuÕQīÕÅśµŹóÕÉÄÕŠŚÕł░ÕQÜz / y = (k + 1) / (k - 1)ŃĆéÕøĀõĖ║zÕÆīyõ║ÆĶ┤©ÕQīĶ┐ÖµĀ»é┐ÖõĖ¬ńŁēÕ╝ÅńÜäĶ¦ŻÕŬĶāĮµś»z = k + 1õĖöy = k - 1ŃĆéĶ┐ÖµĀ’LÜäĶ»Øu = 1ŃĆéÕÅ»õ╗źńÉåĶ¦ŻõžōśqÖõ╣¤µś»õ║ÆĶ┤©ńÜäńēęÄ«ŖµāģÕåĄ(gcd = 1)ŃĆéĶ┐ÖµĀ?x / 2) ^ 2 = u * vÕQīuÕÆīvµ▓Īµ£ēÕģ¼Õģ▒ńÜäĶ┤©ÕøĀµĢ░ÕQīÕøĀµŁżÕ┐ģńäČuÕÆīvķāĮµś»Õ«īÕģ©“qŽx¢╣µĢ░ŃĆéµÄźõĖŗµØźńÜäõ║ŗµāģÕ░▒µ»öĶŠāĮÄĆÕŹĢõ║åÕQīõūou = m ^ 2ÕQīv = n ^ 2ÕQīńäČÕÉÄÕł®ńö©mÕÆīnĶĪ©ńż║xŃĆüyŃĆüzµ£ē’╝Üy = n ^ 2 - m ^ 2ÕQīx = 2 * m * nÕQīz = n ^ 2 + m ^ 2ŃĆéĶ┐ÖµĀĘķóśńø«õĖŁµĢ░µŹ«ĶīāÕø┤1000000ÕQīĶĆīµ×ÜõĖŠmÕÆīnńÜäĶīāÕø┤µ£ĆÕż?000ÕQīĶ┐ÖõĖ¬ÕżŹµØéÕ║”׫▒ÕÅ»õ╗źµÄźÕÅŚõ║åŃĆéµ×ÜõĖäĪÜ䵌ČÕĆÖõĖŹńö©µŗģÕ┐āÕć║ńÄ░ķćŹÕżŹńÜäõ║ÆĶ┤©ńÜäxõĖÄyÕQīÕøĀõĖ°Ö┐ÖķćīxõĖĆիܵś»ÕüȵĢ░ÕQīÕ”éµ×£xÕÆīyÕĘ▓ń╗Åõ║ÆĶ┤©ÕQīķéŻõ╣łyõĖĆիܵś»ÕźćµĢ░ÕQīĶ¦Żµś»Õö»õĖĆńÜäŃĆ?br />ŃĆĆŃĆĆÕŠłÕø¦ńÜ䵜»śqÖõĖ¬ÕĘ¦Õ”ÖńÜäµ¢╣µ│ĢÕ▒ģńäČÕģ¼ÕģāÕēŹ250“q┤Õ░▒µ£ēÕż¦ńēøµā│ÕłŅC║åÕQłõĖóńĢ¬ÕøŠÕQē’╝īÕ«×Õ£©orzÕQ?
sdfond 2009-06-09 09:09 ÕÅæĶĪ©Ķ»äĶ«║
]]>ķÖäPKU 1811õ╗ŻńĀüÕQ?/p>
1 #include <cstdio>
2 #include <stdlib.h>
3 #include <time.h>
4 const int MAX = 8, N = 1000010;
5
6 long long ans, p[N/5];
7 int tag[N];
8
9 long long abs(long long t)
10 {
11 return t < 0 ? -t : t;
12 }
13 void prime()
14 {
15 int cnt = 0;
16
17 for (int i = 2; i < N; i++)
18 {
19 if (!tag[i]) p[cnt++] = i;
20 for (int j = 0; j < cnt && p[j] * i < N; j++)
21 {
22 tag[i*p[j]] = p[j];
23 if (i % p[j] == 0)
24 break;
25 }
26 }
27 }
28 long long gcd(long long a, long long b)
29 {
30 return !b ? a : gcd(b, a % b);
31 }
32 long long MultiMod(long long a, long long b, long long k)
33 {
34 long long ret = 0, tmp = a % k;
35
36 while (b)
37 {
38 if (b & 1)
39 ret = (ret + tmp) % k;
40 tmp = (tmp << 1) % k;
41 b >>= 1;
42 }
43
44 return ret;
45 }
46 long long PowerMod(long long a, long long b, long long k)
47 {
48 long long ret = 1, f = a % k;
49
50 while (b)
51 {
52 if (b & 1)
53 ret = MultiMod(ret, f, k);
54 f = MultiMod(f, f, k);
55 b >>= 1;
56 }
57 return ret;
58 }
59 int TwiceDetect(long long a, long long b, long long k)
60 {
61 int t = 0;
62 long long x, y;
63
64 while ((b & 1) == 0)
65 {
66 b >>= 1;
67 t++;
68 }
69 y = x = PowerMod(a, b, k);
70 while (t--)
71 {
72 y = MultiMod(x, x, k);
73 if (y == 1 && x != 1 && x != k - 1)
74 return 0;
75 x = y;
76 }
77 return y != 1 ? 0 : 1;
78 }
79 bool MillerRabin(long long n)
80 {
81 int i;
82 long long tmp;
83
84 srand(time(0));
85 for (i = 0; i < MAX; i++)
86 {
87 tmp = rand() % (n - 1) + 1;
88 if (TwiceDetect(tmp, n - 1, n) != 1)
89 break;
90 }
91 return (i == MAX);
92 }
93 long long pollard_rho(long long n)
94 {
95 srand(time(0));
96 int i = 1, k = 2;
97 long long d, x = rand() % (n - 1) + 1, y = x;
98 while (true)
99 {
100 i++;
101 x = (MultiMod(x, x, n) - 1) % n;
102 d = abs(gcd(y - x, n));
103 if (d != 1 && d != n)
104 return d;
105 if (i == k)
106 {
107 y = x;
108 k <<= 1;
109 }
110 }
111 }
112 void factorization(long long n)
113 {
114 long long tmp;
115
116 if (n < N)
117 {
118 ans <?= !tag[n] ? n : tag[n];
119 return;
120 }
121 if (MillerRabin(n))
122 {
123 ans <?= n;
124 return;
125 }
126 tmp = pollard_rho(n);
127 factorization(tmp);
128 factorization(n / tmp);
129 }
130
131 int main()
132 {
133 int T;
134 long long n;
135
136 scanf("%d", &T);
137 prime();
138 while (T--)
139 {
140 scanf("%I64d", &n);
141 if (n < N)
142 {
143 if (tag[n] == 0)
144 puts("Prime");
145 else
146 printf("%d\n", tag[n]);
147 continue;
148 }
149 if (MillerRabin(n))
150 puts("Prime");
151 else
152 {
153 ans = 0xfffffffffffffffLL;
154 factorization(n);
155 printf("%I64d\n", ans);
156 }
157 }
158
159 return 0;
160 }
161
sdfond 2009-04-03 20:06 ÕÅæĶĪ©Ķ»äĶ«║
]]>Õ«×ńÄ░ńÜ䵌ČÕĆÖµłæõ╣¤ńŖ»õ║åÕćĀõĖ¬Õ░ÅķöÖ’╝īõĖĆõĖ¬µś»µŖ?0 ^ 15׫æµēōõ║åõĖĆõĖ?ÕQīĶ┐śµ£ēõĖĆõĖ¬Õē¬µ×ØÕ┐ģÖÕšdŖĀÕQÜÕ”éµ×£ÕĮōÕēŹń╗ōµ×£ńÜäŠU”µĢ░õĖ¬µĢ░õĖ║fÕQīķéŻõ╣łÕ”éµ×£n % fõĖŹõžō0ÕQīÕłÖÕē¬µÄēÕQīÕøĀõĖ║ń║”µĢŅCĖ¬µĢ░µś»õ╗źõ╣ś┐U»ńÜäÕģ│ń│╗ń┤»ÕŖĀńÜäŃĆ?br>
1 #include <cstdio>
2 const int M = 14;
3 const long long max = 1000000000000000LL;
4
5 int p[M] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41}, k;
6 long long ans;
7 void solve(long long v, int factor, int pos)
8 {
9 if (factor >= k)
10 {
11 if (factor == k) ans <?= v;
12 return;
13 }
14 if (k % factor) return;
15 if (pos == M) return;
16 for (int i = 1; i <= 50; i++)
17 {
18 v *= p[pos];
19 if (v > max) break;
20 solve(v, factor * (i + 1), pos + 1);
21 }
22 }
23
24 int main()
25 {
26 while (scanf("%d", &k) == 1)
27 {
28 ans = max + 1;
29 solve(1, 1, 0);
30 if (ans > max) printf("-1\n");
31 else printf("%lld\n", ans);
32 }
33
34 return 0;
35 }
36
2 const int M = 14;
3 const long long max = 1000000000000000LL;
4
5 int p[M] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41}, k;
6 long long ans;
7 void solve(long long v, int factor, int pos)
8 {
9 if (factor >= k)
10 {
11 if (factor == k) ans <?= v;
12 return;
13 }
14 if (k % factor) return;
15 if (pos == M) return;
16 for (int i = 1; i <= 50; i++)
17 {
18 v *= p[pos];
19 if (v > max) break;
20 solve(v, factor * (i + 1), pos + 1);
21 }
22 }
23
24 int main()
25 {
26 while (scanf("%d", &k) == 1)
27 {
28 ans = max + 1;
29 solve(1, 1, 0);
30 if (ans > max) printf("-1\n");
31 else printf("%lld\n", ans);
32 }
33
34 return 0;
35 }
36
sdfond 2009-03-30 21:44 ÕÅæĶĪ©Ķ»äĶ«║
]]>Ķ«Šf[i]ĶĪ©ńż║ińÜäń║”µĢ░ÕÆīÕQīe[i]ĶĪ©ńż║ińÜäµ£Ć׫Åń┤ĀÕøĀÕŁÉõĖ¬µĢ░ÕQīt[i]ĶĪ©ńż║(p1 ^ 0 + .. + p1 ^ a1)ÕQīp1µś»tńÜäµ£Ć׫Åń┤ĀÕøĀÕŁÉÕQīa1µś»p1ńÜäÕ╣éŗŲĪ’╝īśqÖµĀĘÕ»╣õ║Äi * p[j]ÕQīÕ”éµ×£p[j]õĖŹµś»ińÜäÕøĀÕŁÉ’╝īķéŻõ╣łµĀęÄŹ«┐U»µĆ¦µØĪõ╗ė×╝īf[i*p[j]] = f[i] * (1 + p[j])ÕQīe[i] = 1ÕQīt[i] = 1 + p[j]ÕQøÕ”éµ×£p[j]µś»ińÜäÕøĀÕŁÉ’╝īķéŻõ╣łńøĖÕĮōõ║Ät[i]ÕżÜõ║åõĖĆÖÕ╣p1 ^ (a1 + 1)ÕQīķ”¢Õģłe[i]++ÕQīńäČÕÉÄtmp = t[i]ÕQīt[i] += p[j] ^ e[i]ÕQīf[i*p[j]] = f[i] / tmp * t[i]ŃĆéĶ┐ÖµĀĘõ╣¤×«▒ÕüÜÕłŅC║åO(1)ńÜ䵌ČķŚ┤Ķ«ĪĮÄŚÕć║õ║åf[i*p[j]]ÕÉīµŚČõ╣¤Ķ«ĪĮÄŚÕć║õ║åķÖäÕŖĀõ┐Īµü»ŃĆ?br>
śqÖń¦Źµ¢ęÄ│ĢśqśÕÅ»õ╗źń涊lŁµÄ©“q┐’╝īõŠŗÕ”éÕÅ»õ╗źĶ«░ÕĮĢińÜäµ£Ć׫Åń┤ĀÕøĀÕŁÉÕQīĶ┐ÖµĀĘÕ░▒ÕÅ»õ╗źÕüÜÕł░O(log n)µŚēÖŚ┤ńÜäń┤ĀÕøĀÕŁÉÕłåĶ¦ŻŃĆ?/p>
sdfond 2009-03-28 15:02 ÕÅæĶĪ©Ķ»äĶ«║
]]> #include <cstdio>
#include <cstdio> const int N = 8;
const int N = 8;
 void extended_gcd(int a, int b, int &x, int &y)
void extended_gcd(int a, int b, int &x, int &y)

 {
{ if (!b)
if (!b)

 {
{ x = 1;
x = 1; y = 0;
y = 0; return;
return; }
} extended_gcd(b, a % b, x, y);
extended_gcd(b, a % b, x, y); int tmp = x;
int tmp = x; x = y;
x = y; y = tmp - a / b * y;
y = tmp - a / b * y; }
}
 int modular_linear_equation_system(int b[N], int m[N], int n)
int modular_linear_equation_system(int b[N], int m[N], int n)

 {
{ int M = 1, x, y, ret = 0;
int M = 1, x, y, ret = 0; for (int i = 0; i < n; i++)
for (int i = 0; i < n; i++) M *= m[i];
M *= m[i]; for (int i = 0; i < n; i++)
for (int i = 0; i < n; i++)

 {
{ extended_gcd(M / m[i], m[i], x, y);
extended_gcd(M / m[i], m[i], x, y); ret += M / m[i] * x * b[i];
ret += M / m[i] * x * b[i]; }
} while (ret <= 0) ret += M;
while (ret <= 0) ret += M; while (ret > M) ret -= M;
while (ret > M) ret -= M;
 return ret;
return ret; }
}
 int main()
int main()

 {
{ int m[N], b[N], T, n, tmp, ans;
int m[N], b[N], T, n, tmp, ans; const int num = 4, numc = 3;
const int num = 4, numc = 3; char str[N], hash[30] = " ABCDEFGHIJKLMNOPQRSTUVWXYZ ";
char str[N], hash[30] = " ABCDEFGHIJKLMNOPQRSTUVWXYZ ";
 scanf("%d", &T);
scanf("%d", &T); while (T--)
while (T--)

 {
{ scanf("%d", &n);
scanf("%d", &n); for (int i = 0; i < num; i++)
for (int i = 0; i < num; i++) scanf("%d", &m[i]);
scanf("%d", &m[i]);
 for (int j = 0; j < n; j++)
for (int j = 0; j < n; j++)

 {
{ scanf("%d", &tmp);
scanf("%d", &tmp); for (int i = 1; i <= num; i++)
for (int i = 1; i <= num; i++)

 {
{ b[num-i] = tmp % 100;
b[num-i] = tmp % 100; tmp /= 100;
tmp /= 100; }
}
 ans = modular_linear_equation_system(b, m, num);
ans = modular_linear_equation_system(b, m, num);
 for (int i = 1; i <= numc; i++)
for (int i = 1; i <= numc; i++)

 {
{ str[numc-i] = hash[ans%100];
str[numc-i] = hash[ans%100]; ans /= 100;
ans /= 100; }
} str[numc] = '\0';
str[numc] = '\0'; if (j == n - 1)
if (j == n - 1)

 {
{ int k = numc - 1;
int k = numc - 1; for (; k >= 0; k--)
for (; k >= 0; k--) if (str[k] != ' ')
if (str[k] != ' ') break;
break; str[k+1] = '\0';
str[k+1] = '\0'; }
} printf("%s", str);
printf("%s", str); }
} putchar('\n');
putchar('\n'); }
}
 return 0;
return 0; }
}
sdfond 2009-03-22 09:51 ÕÅæĶĪ©Ķ»äĶ«║
]]> #include <cstdio>
#include <cstdio> #include <stdlib.h>
#include <stdlib.h> const int MAX = 4, N = 1000000;
const int MAX = 4, N = 1000000;
 long long PowerMod(long long a, long long b, long long k)
long long PowerMod(long long a, long long b, long long k)

 {
{ long long ret = 1, f = a;
long long ret = 1, f = a;
 while (b)
while (b)

 {
{ if (b & 1)
if (b & 1) ret = ret * f % k;
ret = ret * f % k; f = f * f % k;
f = f * f % k; b >>= 1;
b >>= 1; }
} return ret;
return ret; }
} bool MillerRabin(long long n)
bool MillerRabin(long long n)

 {
{ int i;
int i; long long tmp;
long long tmp;
 srand(100);
srand(100); for (i = 0; i < MAX; i++)
for (i = 0; i < MAX; i++)

 {
{ tmp = rand() % (n - 1) + 1;
tmp = rand() % (n - 1) + 1; if (PowerMod(tmp, n - 1, n) != 1)
if (PowerMod(tmp, n - 1, n) != 1) break;
break; }
} return (i == MAX);
return (i == MAX); }
}
 int main()
int main()

 {
{ long long n, i, j;
long long n, i, j;
 bool tag[N] =
bool tag[N] =  {1, 1, 0};
{1, 1, 0};
 for (i = 2; i * i < N; i++)
for (i = 2; i * i < N; i++)

 {
{ if (tag[i]) continue;
if (tag[i]) continue; for (j = i; j * i < N; j++)
for (j = i; j * i < N; j++) tag[j*i] = 1;
tag[j*i] = 1; }
} while (scanf("%lld", &n) == 1)
while (scanf("%lld", &n) == 1)

 {
{ if (n < N)
if (n < N) printf("%s\n", tag[n] ? "NO" : "YES");
printf("%s\n", tag[n] ? "NO" : "YES"); else
else printf("%s\n", ((n & 1) == 0) || !MillerRabin(n) ? "NO" : "YES");
printf("%s\n", ((n & 1) == 0) || !MillerRabin(n) ? "NO" : "YES"); }
}
 return 0;
return 0; }
}
sdfond 2009-03-18 21:15 ÕÅæĶĪ©Ķ»äĶ«║
]]>#include <cstdio>
long long PowerMod(long long a, int b, int k)
{
long long tmp = a, ret = 1;
while (b)
{
if (b & 1)
ret = ret * tmp % k;
tmp = tmp * tmp % k;
b >>= 1;
}
return ret;
}
int main()
{
long long a;
int b, k;
while (scanf("%lld %d %d", &a, &b, &k) == 3)
printf("%lld\n", PowerMod(a, b, k));
return 0;
}
long long PowerMod(long long a, int b, int k)
{
long long tmp = a, ret = 1;
while (b)
{
if (b & 1)
ret = ret * tmp % k;
tmp = tmp * tmp % k;
b >>= 1;
}
return ret;
}
int main()
{
long long a;
int b, k;
while (scanf("%lld %d %d", &a, &b, &k) == 3)
printf("%lld\n", PowerMod(a, b, k));
return 0;
}
sdfond 2009-03-15 10:58 ÕÅæĶĪ©Ķ»äĶ«║
]]>