#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <math.h>
using namespace std;
const int MAX_I = 50010;
const int MAX_J = 20;
int nMax[MAX_I][MAX_J];
int nMin[MAX_I][MAX_J];
int nArr[MAX_I];
int nN, nQ;
void InitRmq(int nN)
{
for (int i = 1; i <= nN; ++i)
{
nMax[i][0] = nMin[i][0] = nArr[i];
}
for (int j = 1; (1 << j) <= nN; ++j)
{
for (int i = 1; i + (1 << j) - 1 <= nN; ++i)
{
nMax[i][j] = max(nMax[i][j - 1],
nMax[i + (1 << (j - 1))][j - 1]);
nMin[i][j] = min(nMin[i][j - 1],
nMin[i + (1 << (j - 1))][j - 1]);
}
}
}
int Query(int nA, int nB)
{
int k = (int)(log(1.0 * nB - nA + 1) / log(2.0));
int nBig = max(nMax[nA][k], nMax[nB - (1 << k) + 1][k]);
int nSml = min(nMin[nA][k], nMin[nB - (1 << k) + 1][k]);
return nBig - nSml;
}
int main()
{
while (scanf("%d%d", &nN, &nQ) == 2)
{
for (int i = 1; i <= nN; ++i)
{
scanf("%d", &nArr[i]);
}
InitRmq(nN);
for (int i = 0; i < nQ; ++i)
{
int nA, nB;
scanf("%d%d", &nA, &nB);
printf("%d\n", Query(nA, nB));
}
}
return 0;
}
#include <string.h>
#include <algorithm>
#include <math.h>
using namespace std;
const int MAX_I = 50010;
const int MAX_J = 20;
int nMax[MAX_I][MAX_J];
int nMin[MAX_I][MAX_J];
int nArr[MAX_I];
int nN, nQ;
void InitRmq(int nN)
{
for (int i = 1; i <= nN; ++i)
{
nMax[i][0] = nMin[i][0] = nArr[i];
}
for (int j = 1; (1 << j) <= nN; ++j)
{
for (int i = 1; i + (1 << j) - 1 <= nN; ++i)
{
nMax[i][j] = max(nMax[i][j - 1],
nMax[i + (1 << (j - 1))][j - 1]);
nMin[i][j] = min(nMin[i][j - 1],
nMin[i + (1 << (j - 1))][j - 1]);
}
}
}
int Query(int nA, int nB)
{
int k = (int)(log(1.0 * nB - nA + 1) / log(2.0));
int nBig = max(nMax[nA][k], nMax[nB - (1 << k) + 1][k]);
int nSml = min(nMin[nA][k], nMin[nB - (1 << k) + 1][k]);
return nBig - nSml;
}
int main()
{
while (scanf("%d%d", &nN, &nQ) == 2)
{
for (int i = 1; i <= nN; ++i)
{
scanf("%d", &nArr[i]);
}
InitRmq(nN);
for (int i = 0; i < nQ; ++i)
{
int nA, nB;
scanf("%d%d", &nA, &nB);
printf("%d\n", Query(nA, nB));
}
}
return 0;
}
yx 2012-10-25 19:29 хшЁЈшЏшЎК
]]>чхцфИфКушЎАхОфЛЅххАБчфКчяММЌцЏцВЁчцяМцГфИхАчАхЈшПфЙхПЋЎБцчНфКу?br /> шЏЅчЎцГщшІщЂхЄчO(N)НIКщДушЏДшЕфhЅцЏчЉКщДцЂцДхЇу?br /> хЄЇцІчцшЕ\цЏх щЂхЄчхНWІфИВхQфЩх ЖцфИоZИфИЊщПхКІфИхЎфихЖцАчфИВушфИНWЌфИфИЊхНW?br />ц?$'хQхшЎ?$'цВЁцхЈхфИВхКчАшПучЖхххЈхцЅчцЏфИЊхчЌІхщЂх фИ'#'хQцххх фИЊ
'#'уцЏхІяМabcЎБхцфК$#a#b#c#учАхЈххЏвАчхНWІфИВqшЁхЄчу?br /> хМфИфИЊцАчцАОlnRad[MAX]хQnRad[i]шЁЈчЄКцюCИВфИчЌЌiфИЊфНО|ЎххЗІшОЙхххОЙхцЖцЉхБ
ђqЖфИфПцхЏЙчЇАчцхЄЇшЗМ RхІццБхоZКnRadцАчЛхяМцфИфИЊчЛшЎКяМnRad[i]-1цАхЅНшЁЈчЄКхфИВ
хЏЙхКчфНО|ЎшНхЄцЉхБчхцхфИВщПхКІушПфИЊчшЏцхQхКшЏЅцЏшОчЎхяМх фицюCИВхКцЌфИцЏхфИВ
ч?хфКхQшфИцюCИВцЏфИфИЊццхНWІфИЄфОЇщНццх Ѕч#хQшПфИЊцОфИЊфОхчфИхАБчЅщцЏшПц ЗфКу?br /> цщшІчцЏхІфНцБхКnRadцАчЛу?br /> цБшПфИЊцАОlчНцГфЙфИЛшІцЏхЉчЈфКфИфКщДцЅчОlшЎКфМхфКnRad[i]чххЇххЙ{цЏхІцфЛЌцБ
nRad[i]чцЖхяМхІцчЅщфКiфЛЅхчnRadхћ|МшфИчЅщфКхщЂцфИфИЊфНО|ЎidхQшНхЄцхЄЇчх?br />фИЄшОЙцЉхБшЗчІЛmaxущЃфЙцфИфИЊчЛшЎКяМnRad[i] шНхЄххЇхфиmin(nRad[2*id - i], max - i)хQ?br />чЖххшПшЁщхЂух ГщЎцЏхІфНшЏцqфИЊхQшПфИЊчшЏцхQхЏЙч ЇхОчхАБхОцИ цЅфКу?br /> шЏцхІфИхQ?br /> хН?mx - i > P[j] чцЖхяМфЛЅS[j]фИоZИхПчхцхфИВх хЋхЈфЛЅS[id]фИоZИхПчхцхфИВфИяМчзК i х?j хЏЙчЇАхQ?br />фЛЅS[i]фИоZИхПчхцхфИВхП чЖх хЋхЈфЛЅS[id]фИоZИхПчхцхфИВфИяМцфЛЅхП ц?P[i] = P[j]хQшЇфИхОу?br />

хН?P[j] > mx - i чцЖхяМфЛЅS[j]фИоZИхПчхцхфИВфИхЎх Јх хЋфКфЛЅS[id]фИоZИхПчхцхфИВфИяМфНцЏхоZК
хЏЙчЇАцЇхЏчЅяМфИхОфИфИЄфИЊчЛПцЁцх хДчщЈхцЏчИхчяМфЙхАБцЏшЏДфЛЅS[i]фИоZИхПчхцхфИВхQх ЖххГш_АфМ?br />цЉхМ хАmxчфНО|ЎяМфЙхАБцЏшЏД P[i] >= mx - iушГфКmxфЙхчщЈхцЏхІхЏЙПUЭМЎБхЊшНшшхЎхЎхЛхw фКу?br />

qфИЊЎоpЏДцхОхОцИ цЅфКууу?br />
фЛЃч хІфИхQ?br />
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX = 110010 * 2;
char szIn[MAX];
char szOut[MAX];
int nRad[MAX];
int Proc(char* pszIn, char* pszOut)
{
int nLen = 1;
*pszOut++ = '$';
while (*pszIn)
{
*pszOut++ = '#';
nLen++;
*pszOut++ = *pszIn++;
nLen++;
}
*pszOut++ = '#';
*pszOut = '\0';
return nLen + 1;
}
void Manacher(int* pnRad, char* pszStr, int nN)
{
int nId = 0, nMax = 0;
//pnRad[0] = 1;
for (int i = 0; i < nN; ++i)
{
if (nMax > i)
{
pnRad[i] = min(pnRad[2 * nId - i], nMax - i);
}
else pnRad[i] = 1;
while (pszStr[i + pnRad[i]] == pszStr[i - pnRad[i]])
{
++pnRad[i];
}
if (pnRad[i] + i > nMax)
{
nMax = pnRad[i] + i;
nId = i;
}
}
}
int main()
{
while (scanf("%s", szIn) == 1)
{
int nLen = Proc(szIn, szOut);
Manacher(nRad, szOut, nLen);
int nAns = 1;
for (int i = 0; i < nLen; ++i)
{
nAns = max(nRad[i], nAns);
}
printf("%d\n", nAns - 1);
}
return 0;
}
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX = 110010 * 2;
char szIn[MAX];
char szOut[MAX];
int nRad[MAX];
int Proc(char* pszIn, char* pszOut)
{
int nLen = 1;
*pszOut++ = '$';
while (*pszIn)
{
*pszOut++ = '#';
nLen++;
*pszOut++ = *pszIn++;
nLen++;
}
*pszOut++ = '#';
*pszOut = '\0';
return nLen + 1;
}
void Manacher(int* pnRad, char* pszStr, int nN)
{
int nId = 0, nMax = 0;
//pnRad[0] = 1;
for (int i = 0; i < nN; ++i)
{
if (nMax > i)
{
pnRad[i] = min(pnRad[2 * nId - i], nMax - i);
}
else pnRad[i] = 1;
while (pszStr[i + pnRad[i]] == pszStr[i - pnRad[i]])
{
++pnRad[i];
}
if (pnRad[i] + i > nMax)
{
nMax = pnRad[i] + i;
nId = i;
}
}
}
int main()
{
while (scanf("%s", szIn) == 1)
{
int nLen = Proc(szIn, szOut);
Manacher(nRad, szOut, nLen);
int nAns = 1;
for (int i = 0; i < nLen; ++i)
{
nAns = max(nRad[i], nAns);
}
printf("%d\n", nAns - 1);
}
return 0;
}
yx 2012-10-24 20:55 хшЁЈшЏшЎК
]]>цфDцфИфИЊщПхКІчхфИВцЖхяМцЏхІщПхКІфИКkхQшНхЄчЈqфИЊkхЏЙheightцАчЛqшЁхчЛхQшПфИЊчННIщЊ
чшЎКцщщЂцфИЊцБфИщх цщKхЄхфИВчфОхшЏДцфКшПфИЊheightцАчЛхчЛчцшЕ\хQфИqцчАхЈ
qцЏфИцфЙчшЇЃууу?br />
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_N = 110;
const int MAX_L = MAX_N * MAX_N;
char szStr[MAX_N];
int nNum[MAX_L];
int nLoc[MAX_L];
bool bVisit[MAX_N];
int sa[MAX_L], rank[MAX_L], height[MAX_L];
int wa[MAX_L], wb[MAX_L], wv[MAX_L], wd[MAX_L];
int cmp(int* r, int a, int b, int l)
{
return r[a] == r[b] && r[a + l] == r[b + l];
}
//ххЂНцГ,rфИКхО хw цАчЛ,nфИКцЛщПхК?mфИКхНWІфИВшхД
void da(int* r, int n, int m)
{
int i, j, p, *x = wa, *y = wb;
for (i = 0; i < m; ++i) wd[i] = 0;
for (i = 0; i < n; ++i) wd[x[i] = r[i]]++;
for (i = 1; i < m; ++i) wd[i] += wd[i - 1];
for (i = n - 1; i >= 0; --i) sa[--wd[x[i]]] = i;
for (j = 1, p = 1; p < n; j *= 2, m = p)
{
for (p = 0, i = n - j; i < n; ++i) y[p++] = i;
for (i = 0; i < n; ++i) if (sa[i] >= j) y[p++] = sa[i] - j;
for (i = 0; i < n; ++i) wv[i] = x[y[i]];
for (i = 0; i < m; ++i) wd[i] = 0;
for (i = 0; i < n; ++i) wd[wv[i]]++;
for (i = 1; i < m; ++i) wd[i] += wd[i - 1];
for (i = n - 1; i >= 0; --i) sa[--wd[wv[i]]] = y[i];
swap(x, y);
for (p = 1, x[sa[0]] = 0, i = 1; i < n; ++i)
{
x[sa[i]] = cmp(y, sa[i - 1], sa[i], j)? p - 1 : p++;
}
}
}
//цБheightцАчЛ
void calHeight(int* r, int n)
{
int i, j, k = 0;
for (i = 1; i <= n; ++i) rank[sa[i]] = i;
for (i = 0; i < n; height[rank[i++]] = k)
{
if (k) --k;
for(j = sa[rank[i] - 1]; r[i + k] == r[j + k]; k++);
}
}
bool Check(int nMid, int nLen, int nN)
{
int nCnt = 0;
memset(bVisit, false, sizeof(bVisit));
for (int i = 2; i <= nLen; ++i)
{
if (nMid > height[i])
{
nCnt = 0;
memset(bVisit, false, sizeof(bVisit));
continue;
}
if (!bVisit[nLoc[sa[i - 1]]])
{
bVisit[nLoc[sa[i - 1]]] = true;
++nCnt;
}
if (!bVisit[nLoc[sa[i]]])
{
bVisit[nLoc[sa[i]]] = true;
++nCnt;
}
if (nCnt == nN) return true;
}
return false;
}
int main()
{
int nT;
scanf("%d", &nT);
while (nT--)
{
int nN;
int nEnd = 300;
int nP = 0;
scanf("%d", &nN);
for (int i = 1; i <= nN; ++i)
{
scanf("%s", szStr);
char* pszStr;
for (pszStr = szStr; *pszStr; ++pszStr)
{
nLoc[nP] = i;
nNum[nP++] = *pszStr;
}
nLoc[nP] = nEnd;
nNum[nP++] = nEnd++;
reverse(szStr, szStr + strlen(szStr));
for (pszStr = szStr; *pszStr; ++pszStr)
{
nLoc[nP] = i;
nNum[nP++] = *pszStr;
}
nLoc[nP] = nEnd;
nNum[nP++] = nEnd++;
}
nNum[nP] = 0;
da(nNum, nP + 1, nEnd);
calHeight(nNum, nP);
int nLeft = 1, nRight = strlen(szStr), nMid;
int nAns = 0;
while (nLeft <= nRight)
{
nMid = (nLeft + nRight) / 2;
if (Check(nMid, nP, nN))
{
nLeft = nMid + 1;
nAns = nMid;
}
else nRight = nMid - 1;
}
printf("%d\n", nAns);
}
return 0;
}
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_N = 110;
const int MAX_L = MAX_N * MAX_N;
char szStr[MAX_N];
int nNum[MAX_L];
int nLoc[MAX_L];
bool bVisit[MAX_N];
int sa[MAX_L], rank[MAX_L], height[MAX_L];
int wa[MAX_L], wb[MAX_L], wv[MAX_L], wd[MAX_L];
int cmp(int* r, int a, int b, int l)
{
return r[a] == r[b] && r[a + l] == r[b + l];
}
//ххЂНцГ,rфИКхО хw цАчЛ,nфИКцЛщПхК?mфИКхНWІфИВшхД
void da(int* r, int n, int m)
{
int i, j, p, *x = wa, *y = wb;
for (i = 0; i < m; ++i) wd[i] = 0;
for (i = 0; i < n; ++i) wd[x[i] = r[i]]++;
for (i = 1; i < m; ++i) wd[i] += wd[i - 1];
for (i = n - 1; i >= 0; --i) sa[--wd[x[i]]] = i;
for (j = 1, p = 1; p < n; j *= 2, m = p)
{
for (p = 0, i = n - j; i < n; ++i) y[p++] = i;
for (i = 0; i < n; ++i) if (sa[i] >= j) y[p++] = sa[i] - j;
for (i = 0; i < n; ++i) wv[i] = x[y[i]];
for (i = 0; i < m; ++i) wd[i] = 0;
for (i = 0; i < n; ++i) wd[wv[i]]++;
for (i = 1; i < m; ++i) wd[i] += wd[i - 1];
for (i = n - 1; i >= 0; --i) sa[--wd[wv[i]]] = y[i];
swap(x, y);
for (p = 1, x[sa[0]] = 0, i = 1; i < n; ++i)
{
x[sa[i]] = cmp(y, sa[i - 1], sa[i], j)? p - 1 : p++;
}
}
}
//цБheightцАчЛ
void calHeight(int* r, int n)
{
int i, j, k = 0;
for (i = 1; i <= n; ++i) rank[sa[i]] = i;
for (i = 0; i < n; height[rank[i++]] = k)
{
if (k) --k;
for(j = sa[rank[i] - 1]; r[i + k] == r[j + k]; k++);
}
}
bool Check(int nMid, int nLen, int nN)
{
int nCnt = 0;
memset(bVisit, false, sizeof(bVisit));
for (int i = 2; i <= nLen; ++i)
{
if (nMid > height[i])
{
nCnt = 0;
memset(bVisit, false, sizeof(bVisit));
continue;
}
if (!bVisit[nLoc[sa[i - 1]]])
{
bVisit[nLoc[sa[i - 1]]] = true;
++nCnt;
}
if (!bVisit[nLoc[sa[i]]])
{
bVisit[nLoc[sa[i]]] = true;
++nCnt;
}
if (nCnt == nN) return true;
}
return false;
}
int main()
{
int nT;
scanf("%d", &nT);
while (nT--)
{
int nN;
int nEnd = 300;
int nP = 0;
scanf("%d", &nN);
for (int i = 1; i <= nN; ++i)
{
scanf("%s", szStr);
char* pszStr;
for (pszStr = szStr; *pszStr; ++pszStr)
{
nLoc[nP] = i;
nNum[nP++] = *pszStr;
}
nLoc[nP] = nEnd;
nNum[nP++] = nEnd++;
reverse(szStr, szStr + strlen(szStr));
for (pszStr = szStr; *pszStr; ++pszStr)
{
nLoc[nP] = i;
nNum[nP++] = *pszStr;
}
nLoc[nP] = nEnd;
nNum[nP++] = nEnd++;
}
nNum[nP] = 0;
da(nNum, nP + 1, nEnd);
calHeight(nNum, nP);
int nLeft = 1, nRight = strlen(szStr), nMid;
int nAns = 0;
while (nLeft <= nRight)
{
nMid = (nLeft + nRight) / 2;
if (Check(nMid, nP, nN))
{
nLeft = nMid + 1;
nAns = nMid;
}
else nRight = nMid - 1;
}
printf("%d\n", nAns);
}
return 0;
}
yx 2012-10-23 21:11 хшЁЈшЏшЎК
]]>хЏЙхКчхНWІфИВфИчНWЌi-1фИЊхНWІуххМхЇфИчДцВЁхчАqфИЊbugушфИцГЈцфИщфИшНш{ПUеdА
хw цхччЖцфИхЛяМхЄх х фИЊцЁфgцЇхЖх_ЏфКууу?br /> шНЌчЇЛцЙчЈхQdp[i][j] = min(dp[i][j], dp[i-1][nNext] + szText[i-1] != k)хQх ЖфИnNext
цЏфЛчЖцjхЏфЛЅшНЌчЇЛхАчщхЙщ цхччЖцяМkфЛЃшЁЈчхНхшОЙчцу?br />
фЛЃч хІфИхQ?br />
#include <stdio.h>
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
const int MAX_N = 61;
const int MAX_L = 31;
const int MAX_D = 4;
const int INF = 1110;
char chHash[256];
char szPat[MAX_L];
void InitHash()
{
chHash['A'] = 0;
chHash['G'] = 1;
chHash['C'] = 2;
chHash['T'] = 3;
}
struct Trie
{
Trie* fail;
Trie* next[MAX_D];
bool flag;
int no;
};
int nP;
Trie* pRoot;
Trie tries[MAX_N * MAX_L];
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(Trie* pRoot, char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
int idx = chHash[*pszPat];
if (pNode->next[idx] == NULL)
{
pNode->next[idx] = NewNode();
}
pNode = pNode->next[idx];
++pszPat;
}
pNode->flag = true;
}
void BuildAC(Trie* pRoot)
{
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < MAX_D; ++i)
{
if (front->next[i])
{
Trie* pNode = front->fail;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
front->next[i]->flag |= front->next[i]->fail->flag;
qt.push(front->next[i]);
}
else
{
front->next[i] = front == pRoot? pRoot : front->fail->next[i];
}
}
}
}
int nChange[INF][INF];
char szText[INF];
int Solve()
{
int nLen = strlen(szText);
for (int i = 0; i <= nLen; ++i)
{
for (int j = 0; j < nP; ++j)
{
nChange[i][j] = INF;
}
}
int i, j, k;
nChange[0][0] = 0;
for (i = 1; i <= nLen; ++i)
{
for (j = 0; j < nP; ++j)
{
if (tries[j].flag) continue;
if (nChange[i - 1][j] == INF) continue;
for (k = 0; k < MAX_D; ++k)
{
int nNext = tries[j].next[k] - tries;
if (tries[nNext].flag) continue;
//trieцЏшОЙцц ,цфЛЅiцЏфЛ1хАlen,шфИхНххчЌІцЏszText[i-1]
int nTemp = nChange[i - 1][j] + (k != chHash[szText[i - 1]]);
nChange[i][nNext] = min(nChange[i][nNext], nTemp);
}
}
}
int nAns = INF;
for (i = 0; i < nP; ++i)
{
if (!tries[i].flag)
nAns = min(nAns, nChange[nLen][i]);
}
return nAns == INF? -1 : nAns;
}
int main()
{
int nN;
int nCase = 1;
InitHash();
while (scanf("%d", &nN), nN)
{
InitTrie(pRoot);
while (nN--)
{
scanf("%s", szPat);
Insert(pRoot, szPat);
}
BuildAC(pRoot);
scanf("%s", szText);
printf("Case %d: %d\n", nCase++, Solve());
}
return 0;
}
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
const int MAX_N = 61;
const int MAX_L = 31;
const int MAX_D = 4;
const int INF = 1110;
char chHash[256];
char szPat[MAX_L];
void InitHash()
{
chHash['A'] = 0;
chHash['G'] = 1;
chHash['C'] = 2;
chHash['T'] = 3;
}
struct Trie
{
Trie* fail;
Trie* next[MAX_D];
bool flag;
int no;
};
int nP;
Trie* pRoot;
Trie tries[MAX_N * MAX_L];
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(Trie* pRoot, char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
int idx = chHash[*pszPat];
if (pNode->next[idx] == NULL)
{
pNode->next[idx] = NewNode();
}
pNode = pNode->next[idx];
++pszPat;
}
pNode->flag = true;
}
void BuildAC(Trie* pRoot)
{
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < MAX_D; ++i)
{
if (front->next[i])
{
Trie* pNode = front->fail;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
front->next[i]->flag |= front->next[i]->fail->flag;
qt.push(front->next[i]);
}
else
{
front->next[i] = front == pRoot? pRoot : front->fail->next[i];
}
}
}
}
int nChange[INF][INF];
char szText[INF];
int Solve()
{
int nLen = strlen(szText);
for (int i = 0; i <= nLen; ++i)
{
for (int j = 0; j < nP; ++j)
{
nChange[i][j] = INF;
}
}
int i, j, k;
nChange[0][0] = 0;
for (i = 1; i <= nLen; ++i)
{
for (j = 0; j < nP; ++j)
{
if (tries[j].flag) continue;
if (nChange[i - 1][j] == INF) continue;
for (k = 0; k < MAX_D; ++k)
{
int nNext = tries[j].next[k] - tries;
if (tries[nNext].flag) continue;
//trieцЏшОЙцц ,цфЛЅiцЏфЛ1хАlen,шфИхНххчЌІцЏszText[i-1]
int nTemp = nChange[i - 1][j] + (k != chHash[szText[i - 1]]);
nChange[i][nNext] = min(nChange[i][nNext], nTemp);
}
}
}
int nAns = INF;
for (i = 0; i < nP; ++i)
{
if (!tries[i].flag)
nAns = min(nAns, nChange[nLen][i]);
}
return nAns == INF? -1 : nAns;
}
int main()
{
int nN;
int nCase = 1;
InitHash();
while (scanf("%d", &nN), nN)
{
InitTrie(pRoot);
while (nN--)
{
scanf("%s", szPat);
Insert(pRoot, szPat);
}
BuildAC(pRoot);
scanf("%s", szText);
printf("Case %d: %d\n", nCase++, Solve());
}
return 0;
}
yx 2012-10-21 16:53 хшЁЈшЏшЎК
]]>чшхДхЏшНцЏ-128х?27цш?х?55хQшПфИЊцЏц вЎО~шЏхЈфИхчуцфЛЅяМчДцЅчЈхНWІфИВ
цАчЛшЏеd ЅцАцЎхщшІххЄчфИухЏфЛЅчДцЅхАцЏфИЊхчЌІх?28хххЄчу?br /> хІхЄхQgetcharqхчцЏintхQфНцЏфИgetsфЙчБЛчхНцАшЗхОчхМчхЗЎхЋфЙфИцЏщЃфЙчЁЎхЎчфКу?br />цшЇхОgetcharщЄфКхЏЙeofфЙхЄх ЖфНщНшПхцЃхЙ{фНцЏяМхІцcharцЏцНWІхЗчшЏхQscanfцш?br />getsфЙчБЛхОхАчcharцАчЛщщЂхЏшНЎБх хЋшДхщgКууу?br /> qфИЊхЏфЛЅчцщцКцфgхQхчЈgetcharшЏеd ЅђqЖчЈ%dшОхКх ЖшПххМщЊшЏфИущЊшЏчЈхКхІфИяМ
цГЈщцчщЈхцЏчцщцКцфЛЖчщЈху?br />
#include <stdio.h>
#include <stdlib.h>
int main()
{
char ch;
freopen("in.txt", "r", stdin);
//freopen("in.txt", "w", stdout);
int nNum = 100;
int nCh;
do
{
printf("%d\n", nCh = getchar());
}while (nCh != EOF);
/*while (nNum--)
{
putchar(rand() % 256);
}*/
return 0;
}
#include <stdlib.h>
int main()
{
char ch;
freopen("in.txt", "r", stdin);
//freopen("in.txt", "w", stdout);
int nNum = 100;
int nCh;
do
{
printf("%d\n", nCh = getchar());
}while (nCh != EOF);
/*while (nNum--)
{
putchar(rand() % 256);
}*/
return 0;
}
шЏЅщЂчфЛЃч хІфИяМ
#include <stdio.h>
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
const int MAX_D = 256;
const int MAX_N = 51;
const int MAX_M = 51;
const int MAX_P = 11;
struct Trie
{
Trie* fail;
Trie* next[MAX_D];
int no;
bool flag;
};
Trie tries[MAX_P * MAX_P];
int nP;
int nN, nM;
Trie* pRoot;
int nHash[MAX_D];
char szPat[MAX_M];
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(Trie* pRoot, char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
int idx = nHash[*pszPat];
if (pNode->next[idx] == NULL)
{
pNode->next[idx] = NewNode();
}
pNode = pNode->next[idx];
++pszPat;
}
pNode->flag = true;
}
void BuildAC(Trie* pRoot)
{
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < nN; ++i)
{
if (front->next[i])
{
Trie* pNode = front;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
front->next[i]->flag |= front->next[i]->fail->flag;
qt.push(front->next[i]);
}
else
{
front->next[i] = front->fail->next[i];
}
}
}
}
const int MAX_L = 200;
struct BigInt
{
int nD[MAX_L];
BigInt()
{
Clear();
}
void Clear()
{
memset(nD, 0, sizeof(nD));
}
void Print()
{
int i = MAX_L - 1;
while (!nD[i] && i)--i;
while (i >= 0)
{
putchar(nD[i] + '0');
--i;
}
}
int operator[](int idx) const
{
return nD[idx];
}
int& operator[](int idx)
{
return nD[idx];
}
};
BigInt bi[MAX_M][MAX_D];
BigInt operator+(const BigInt& one, const BigInt& two)
{
BigInt ret;
for (int i = 0, nAdd = 0; i < MAX_L; ++i)
{
ret[i] = one[i] + two[i] + nAdd;
nAdd = ret[i] / 10;
ret[i] %= 10;
}
return ret;
}
void Solve()
{
BigInt ans;
for (int i = 0; i <= nM; ++i)
{
for (int j = 0; j < nP; ++j)
{
bi[i][j].Clear();
}
}
bi[0][0][0] = 1;
for (int i = 1; i <= nM; ++i)
{
for (int j = 0; j < nP; ++j)
{
if (tries[j].flag) continue;
for (int k = 0; k < nN; ++k)
{
int nNext = tries[j].next[k] - tries;
if (tries[nNext].flag == false)
{
bi[i][nNext] = bi[i][nNext] + bi[i - 1][j];
}
}
}
}
for (int i = 0; i < nP; ++i)
{
ans = ans + bi[nM][i];
}
ans.Print();
printf("\n");
}
int main()
{
int nT;
while (scanf("%d%d%d%*c", &nN, &nM, &nT) == 3)
{
int nCh;
int nTmp = 0;
memset(nHash, 0, sizeof(nHash));
while (nCh = getchar(), nCh != '\n')
{
if (!nHash[nCh])
{
nHash[nCh] = nTmp++;
}
}
InitTrie(pRoot);
while (nT--)
{
gets(szPat);
Insert(pRoot, szPat);
}
printf("1");
BuildAC(pRoot);
printf("2");
Solve();
}
return 0;
}
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
const int MAX_D = 256;
const int MAX_N = 51;
const int MAX_M = 51;
const int MAX_P = 11;
struct Trie
{
Trie* fail;
Trie* next[MAX_D];
int no;
bool flag;
};
Trie tries[MAX_P * MAX_P];
int nP;
int nN, nM;
Trie* pRoot;
int nHash[MAX_D];
char szPat[MAX_M];
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(Trie* pRoot, char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
int idx = nHash[*pszPat];
if (pNode->next[idx] == NULL)
{
pNode->next[idx] = NewNode();
}
pNode = pNode->next[idx];
++pszPat;
}
pNode->flag = true;
}
void BuildAC(Trie* pRoot)
{
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < nN; ++i)
{
if (front->next[i])
{
Trie* pNode = front;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
front->next[i]->flag |= front->next[i]->fail->flag;
qt.push(front->next[i]);
}
else
{
front->next[i] = front->fail->next[i];
}
}
}
}
const int MAX_L = 200;
struct BigInt
{
int nD[MAX_L];
BigInt()
{
Clear();
}
void Clear()
{
memset(nD, 0, sizeof(nD));
}
void Print()
{
int i = MAX_L - 1;
while (!nD[i] && i)--i;
while (i >= 0)
{
putchar(nD[i] + '0');
--i;
}
}
int operator[](int idx) const
{
return nD[idx];
}
int& operator[](int idx)
{
return nD[idx];
}
};
BigInt bi[MAX_M][MAX_D];
BigInt operator+(const BigInt& one, const BigInt& two)
{
BigInt ret;
for (int i = 0, nAdd = 0; i < MAX_L; ++i)
{
ret[i] = one[i] + two[i] + nAdd;
nAdd = ret[i] / 10;
ret[i] %= 10;
}
return ret;
}
void Solve()
{
BigInt ans;
for (int i = 0; i <= nM; ++i)
{
for (int j = 0; j < nP; ++j)
{
bi[i][j].Clear();
}
}
bi[0][0][0] = 1;
for (int i = 1; i <= nM; ++i)
{
for (int j = 0; j < nP; ++j)
{
if (tries[j].flag) continue;
for (int k = 0; k < nN; ++k)
{
int nNext = tries[j].next[k] - tries;
if (tries[nNext].flag == false)
{
bi[i][nNext] = bi[i][nNext] + bi[i - 1][j];
}
}
}
}
for (int i = 0; i < nP; ++i)
{
ans = ans + bi[nM][i];
}
ans.Print();
printf("\n");
}
int main()
{
int nT;
while (scanf("%d%d%d%*c", &nN, &nM, &nT) == 3)
{
int nCh;
int nTmp = 0;
memset(nHash, 0, sizeof(nHash));
while (nCh = getchar(), nCh != '\n')
{
if (!nHash[nCh])
{
nHash[nCh] = nTmp++;
}
}
InitTrie(pRoot);
while (nT--)
{
gets(szPat);
Insert(pRoot, szPat);
}
printf("1");
BuildAC(pRoot);
printf("2");
Solve();
}
return 0;
}
yx 2012-10-20 21:01 хшЁЈшЏшЎК
]]>qцЏчЈцЈЁхМфИВхЛКчЋTrieхОяМц вЎTrieхжОчЋшvшЗЏхОщПхКІфИ?ччЉщЕMу?br /> цРL х|АчЎфи26^1+26^2+...+26^LуфИхЋцЈЁхМфИВчц х|РLАфИКчЉщЕN = M^1+M^2+M^3
+...+M^LччЌЌфИшЁфЙхуцРL х|АчЎххжMИхЋцЈЁхМфИВчц хЕхАБцЏчцЁу?br /> qщчЈхАфКчЉщыфИфКчЎцГяМцЏхІхПЋщхЅхQшПцхПЋщхЅцБхуфНцЏяМцчЈфКцфНчЌІщшВхQццВхЇ
чцЏщшВхчцфННWІцВЁцфМх чёхQшцqхНфНцфМх ОUЇчхЈчЈхQцфЛЅцВхЇфКуууфИчДц ЗфОщНqфИ
х RууххQцхцхчАфКшПфИЊщЎщЂууухфК?60шЁхЗІхГчфЛЃч хQхщЂчфИщЈхфЛЃч хЏфЛЅхНфНч?br />щ|фНчцЈЁцПфКуууTrieхЁфЙфИщяМqх хЄЉфМАшЎЁхОцхАфИцЅчЈфКууу?br />
фЛЃч хІфИхQ?br />
#include <stdio.h>
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
typedef unsigned long long INT;
const int MAX_D = 26;
const int MAX_L = 10;
const int MAX_N = 10;
char szPat[MAX_L];
const int MAX_S = 31;
struct Matrix
{
int nSize;
INT nD[MAX_S][MAX_S];
Matrix(int nS)
{
Clear(nS);
}
Matrix& operator = (const Matrix& m)
{
nSize = m.nSize;
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
nD[i][j] = m.nD[i][j];
}
}
return *this;
}
void Clear(int nS)
{
nSize = nS;
memset(nD, 0, sizeof(nD));
}
void Unit()
{
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
nD[i][j] = (i == j ? 1 : 0);
}
}
}
};
Matrix operator+(const Matrix& A, const Matrix& B)
{
Matrix C(A.nSize);
for (int i = 0; i < A.nSize; ++i)
{
for (int j = 0; j < A.nSize; ++j)
{
C.nD[i][j] = A.nD[i][j] + B.nD[i][j];
}
}
return C;
}
Matrix operator*(const Matrix& nA, const Matrix& nB)
{
Matrix nC(nB.nSize);
for (int i = 0; i < nA.nSize; ++i)
{
for (int j = 0; j < nA.nSize; ++j)
{
for (int k = 0; k < nA.nSize; ++k)
{
nC.nD[i][j] += nA.nD[i][k] * nB.nD[k][j];
}
}
}
return nC;
}
Matrix operator^(Matrix B, INT nExp)
{
Matrix ans(B.nSize);
ans.Unit();
while (nExp)
{
if (nExp % 2)
{
ans = ans * B;
}
B = B * B;
nExp >>= 1;
}
return ans;
}
//цБbase^1+base^2+ +base^N
+base^N
Matrix SumPowMatrix(Matrix& base, INT nN)
{
if (nN == 1)
{
return base;
}
Matrix ans = SumPowMatrix(base, nN / 2);
ans = ans + ((base^(nN / 2)) * ans);//щшВqчЎНWІфПшЏфИфКфМх чё
if (nN % 2)
{
ans = ans + (base^nN);//цВЁфМх чёх?хП щЁЛх цЌх?цЅщ2фИЊхАцЖфК
}
return ans;
}
struct Trie
{
Trie* next[MAX_D];
Trie* fail;
int no;
bool flag;
};
Trie tries[MAX_L * MAX_N];
int nP;
Trie* pRoot;
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(Trie* pRoot, char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
int idx = *pszPat - 'a';
if (pNode->next[idx] == NULL)
{
pNode->next[idx] = NewNode();
}
pNode = pNode->next[idx];
++pszPat;
}
pNode->flag = true;
}
void BuildAC(Trie* pRoot, Matrix& M)
{
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
M.Clear(nP);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < MAX_D; ++i)
{
if (front->next[i])
{
Trie* pNode = front->fail;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
if (front->next[i]->fail->flag)
{
front->next[i]->flag = true;
}
qt.push(front->next[i]);
}
else
{
front->next[i] = front == pRoot? pRoot : front->fail->next[i];
}
//qщхП щЁЛшІх фИfront->flagфИКfalseчхЄцфЙ?х фИх фМчцфИхччЉщ?/span>
if (!front->next[i]->flag)
{
++M.nD[front->no][front->next[i]->no];
}
}
}
}
int main()
{
int nN;
INT nL;
Matrix M(0);
while (scanf("%d%I64u", &nN, &nL) == 2)
{
InitTrie(pRoot);
while (nN--)
{
scanf("%s", szPat);
Insert(pRoot, szPat);
}
BuildAC(pRoot, M);
Matrix tmp(1);
tmp.nD[0][0] = 26;
tmp = SumPowMatrix(tmp, nL);
INT nAns = tmp.nD[0][0];
Matrix msum = SumPowMatrix(M, nL);
for (int i = 0; i < msum.nSize; ++i)
{
nAns -= msum.nD[0][i];
}
printf("%I64u\n", nAns);
}
return 0;
}
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
typedef unsigned long long INT;
const int MAX_D = 26;
const int MAX_L = 10;
const int MAX_N = 10;
char szPat[MAX_L];
const int MAX_S = 31;
struct Matrix
{
int nSize;
INT nD[MAX_S][MAX_S];
Matrix(int nS)
{
Clear(nS);
}
Matrix& operator = (const Matrix& m)
{
nSize = m.nSize;
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
nD[i][j] = m.nD[i][j];
}
}
return *this;
}
void Clear(int nS)
{
nSize = nS;
memset(nD, 0, sizeof(nD));
}
void Unit()
{
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
nD[i][j] = (i == j ? 1 : 0);
}
}
}
};
Matrix operator+(const Matrix& A, const Matrix& B)
{
Matrix C(A.nSize);
for (int i = 0; i < A.nSize; ++i)
{
for (int j = 0; j < A.nSize; ++j)
{
C.nD[i][j] = A.nD[i][j] + B.nD[i][j];
}
}
return C;
}
Matrix operator*(const Matrix& nA, const Matrix& nB)
{
Matrix nC(nB.nSize);
for (int i = 0; i < nA.nSize; ++i)
{
for (int j = 0; j < nA.nSize; ++j)
{
for (int k = 0; k < nA.nSize; ++k)
{
nC.nD[i][j] += nA.nD[i][k] * nB.nD[k][j];
}
}
}
return nC;
}
Matrix operator^(Matrix B, INT nExp)
{
Matrix ans(B.nSize);
ans.Unit();
while (nExp)
{
if (nExp % 2)
{
ans = ans * B;
}
B = B * B;
nExp >>= 1;
}
return ans;
}
//цБbase^1+base^2+
 +base^N
+base^NMatrix SumPowMatrix(Matrix& base, INT nN)
{
if (nN == 1)
{
return base;
}
Matrix ans = SumPowMatrix(base, nN / 2);
ans = ans + ((base^(nN / 2)) * ans);//щшВqчЎНWІфПшЏфИфКфМх чё
if (nN % 2)
{
ans = ans + (base^nN);//цВЁфМх чёх?хП щЁЛх цЌх?цЅщ2фИЊхАцЖфК
}
return ans;
}
struct Trie
{
Trie* next[MAX_D];
Trie* fail;
int no;
bool flag;
};
Trie tries[MAX_L * MAX_N];
int nP;
Trie* pRoot;
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(Trie* pRoot, char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
int idx = *pszPat - 'a';
if (pNode->next[idx] == NULL)
{
pNode->next[idx] = NewNode();
}
pNode = pNode->next[idx];
++pszPat;
}
pNode->flag = true;
}
void BuildAC(Trie* pRoot, Matrix& M)
{
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
M.Clear(nP);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < MAX_D; ++i)
{
if (front->next[i])
{
Trie* pNode = front->fail;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
if (front->next[i]->fail->flag)
{
front->next[i]->flag = true;
}
qt.push(front->next[i]);
}
else
{
front->next[i] = front == pRoot? pRoot : front->fail->next[i];
}
//qщхП щЁЛшІх фИfront->flagфИКfalseчхЄцфЙ?х фИх фМчцфИхччЉщ?/span>
if (!front->next[i]->flag)
{
++M.nD[front->no][front->next[i]->no];
}
}
}
}
int main()
{
int nN;
INT nL;
Matrix M(0);
while (scanf("%d%I64u", &nN, &nL) == 2)
{
InitTrie(pRoot);
while (nN--)
{
scanf("%s", szPat);
Insert(pRoot, szPat);
}
BuildAC(pRoot, M);
Matrix tmp(1);
tmp.nD[0][0] = 26;
tmp = SumPowMatrix(tmp, nL);
INT nAns = tmp.nD[0][0];
Matrix msum = SumPowMatrix(M, nL);
for (int i = 0; i < msum.nSize; ++i)
{
nAns -= msum.nD[0][i];
}
printf("%I64u\n", nAns);
}
return 0;
}
yx 2012-10-18 22:02 хшЁЈшЏшЎК
]]>цхЅНчшЇЃухІACшЊхЈцКцTrieхжАБшоpДЙфКшП2хЄЉфКхQчЖххМцшПфИЊщЂхцЏфИхЄЉяМхЅНхЈхКцЌцчНфКу?br /> щЉЌфИхПЋцЏшЕфКхQфЛщПцЅцЂхАщхфЙфИчЅщцЏхЅНцЏхууушПцЏхМБшхууу?br /> шДДфИцчTrieх?хПЋщхЅ(чДцЅфКхфК?цВЁцхццАшЎКщщЂщЃчЇНцГ)...
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long INT;
const int MOD = 100000;
const int MAX_P = 100;
const int MAX_D = 4;
int nIdx[256];
char szPat[MAX_P];
INT nMatrix[MAX_P][MAX_P];
INT B[MAX_P][MAX_P];
INT A[MAX_P][MAX_P];
void InitIdx()
{
nIdx['A'] = 0;
nIdx['C'] = 1;
nIdx['T'] = 2;
nIdx['G'] = 3;
}
struct Trie
{
Trie* fail;
Trie* next[MAX_D];
int no;
bool flag;
Trie()
{
fail = NULL;
memset(next, 0, sizeof(next));
no = 0;
flag = false;
}
};
Trie tries[MAX_D * MAX_P];
int nP;
Trie* pRoot;
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
if (pNode->next[nIdx[*pszPat]] == NULL)
{
pNode->next[nIdx[*pszPat]] = NewNode();
}
pNode = pNode->next[nIdx[*pszPat]];
++pszPat;
}
pNode->flag = true;
}
int BuildAC(Trie* pRoot)
{
memset(nMatrix, 0, sizeof(nMatrix));
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < MAX_D; ++i)
{
if (front->next[i])
{
Trie* pNode = front->fail;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
if (front->next[i]->fail->flag == true)
{
front->next[i]->flag = true;
}
qt.push(front->next[i]);
}
else
{
front->next[i] = front == pRoot? pRoot : front->fail->next[i];
}
if (front->next[i]->flag == false)
{
nMatrix[front->no][front->next[i]->no]++;
}
}
}
return nP;//шчЙцжMИЊц?/span>
}
void MultyMatrix(INT A[][MAX_P], INT B[][MAX_P], INT C[][MAX_P], int nSize)
{
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
INT nSum = 0;
for (int k = 0; k < nSize; ++k)
{
nSum = (nSum + A[i][k] * B[k][j]) % MOD;
}
C[i][j] = nSum;
}
}
}
void CopyMatrix(INT A[][MAX_P], INT B[][MAX_P], int nSize)
{
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
A[i][j] = B[i][j];
}
}
}
void MatrixPower(INT M[][MAX_P], int nSize, INT nP)
{
if (nP == 1)
{
CopyMatrix(A, M, nSize);
return;
}
MatrixPower(M, nSize, nP / 2);
MultyMatrix(A, A, B, nSize);
if (nP % 2)
{
MultyMatrix(B, M, A, nSize);
}
else
{
CopyMatrix(A, B, nSize);
}
}
int main()
{
INT nM, nN;
InitIdx();
while (scanf("%I64d%I64d", &nM, &nN) == 2)
{
InitTrie(pRoot);
while (nM--)
{
scanf("%s", szPat);
Insert(szPat);
}
int nSize = BuildAC(pRoot);
MatrixPower(nMatrix, nSize, nN);
INT nAns = 0;
for (int i = 0; i < nSize; ++i)
{
nAns = (nAns + A[0][i]) % MOD;
}
printf("%I64d\n", nAns % MOD);
}
return 0;
}
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long INT;
const int MOD = 100000;
const int MAX_P = 100;
const int MAX_D = 4;
int nIdx[256];
char szPat[MAX_P];
INT nMatrix[MAX_P][MAX_P];
INT B[MAX_P][MAX_P];
INT A[MAX_P][MAX_P];
void InitIdx()
{
nIdx['A'] = 0;
nIdx['C'] = 1;
nIdx['T'] = 2;
nIdx['G'] = 3;
}
struct Trie
{
Trie* fail;
Trie* next[MAX_D];
int no;
bool flag;
Trie()
{
fail = NULL;
memset(next, 0, sizeof(next));
no = 0;
flag = false;
}
};
Trie tries[MAX_D * MAX_P];
int nP;
Trie* pRoot;
Trie* NewNode()
{
memset(&tries[nP], 0, sizeof(Trie));
tries[nP].no = nP;
return &tries[nP++];
}
void InitTrie(Trie*& pRoot)
{
nP = 0;
pRoot = NewNode();
}
void Insert(char* pszPat)
{
Trie* pNode = pRoot;
while (*pszPat)
{
if (pNode->next[nIdx[*pszPat]] == NULL)
{
pNode->next[nIdx[*pszPat]] = NewNode();
}
pNode = pNode->next[nIdx[*pszPat]];
++pszPat;
}
pNode->flag = true;
}
int BuildAC(Trie* pRoot)
{
memset(nMatrix, 0, sizeof(nMatrix));
pRoot->fail = NULL;
queue<Trie*> qt;
qt.push(pRoot);
while (!qt.empty())
{
Trie* front = qt.front();
qt.pop();
for (int i = 0; i < MAX_D; ++i)
{
if (front->next[i])
{
Trie* pNode = front->fail;
while (pNode && pNode->next[i] == NULL)
{
pNode = pNode->fail;
}
front->next[i]->fail = pNode? pNode->next[i] : pRoot;
if (front->next[i]->fail->flag == true)
{
front->next[i]->flag = true;
}
qt.push(front->next[i]);
}
else
{
front->next[i] = front == pRoot? pRoot : front->fail->next[i];
}
if (front->next[i]->flag == false)
{
nMatrix[front->no][front->next[i]->no]++;
}
}
}
return nP;//шчЙцжMИЊц?/span>
}
void MultyMatrix(INT A[][MAX_P], INT B[][MAX_P], INT C[][MAX_P], int nSize)
{
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
INT nSum = 0;
for (int k = 0; k < nSize; ++k)
{
nSum = (nSum + A[i][k] * B[k][j]) % MOD;
}
C[i][j] = nSum;
}
}
}
void CopyMatrix(INT A[][MAX_P], INT B[][MAX_P], int nSize)
{
for (int i = 0; i < nSize; ++i)
{
for (int j = 0; j < nSize; ++j)
{
A[i][j] = B[i][j];
}
}
}
void MatrixPower(INT M[][MAX_P], int nSize, INT nP)
{
if (nP == 1)
{
CopyMatrix(A, M, nSize);
return;
}
MatrixPower(M, nSize, nP / 2);
MultyMatrix(A, A, B, nSize);
if (nP % 2)
{
MultyMatrix(B, M, A, nSize);
}
else
{
CopyMatrix(A, B, nSize);
}
}
int main()
{
INT nM, nN;
InitIdx();
while (scanf("%I64d%I64d", &nM, &nN) == 2)
{
InitTrie(pRoot);
while (nM--)
{
scanf("%s", szPat);
Insert(szPat);
}
int nSize = BuildAC(pRoot);
MatrixPower(nMatrix, nSize, nN);
INT nAns = 0;
for (int i = 0; i < nSize; ++i)
{
nAns = (nAns + A[0][i]) % MOD;
}
printf("%I64d\n", nAns % MOD);
}
return 0;
}
yx 2012-10-18 09:46 хшЁЈшЏшЎК
]]>qчЇОcжMММцЃхшЁЈшООхМчхчЌІфИВхАБхЎвхКщхЄфКу?br />
чжКІчЁЇчDFAхЎфЙхІфИхQ?br /> шБцх ЈчЇАхQDeterministic Finite Automaton, НхяМDFA
ууDFAхЎфЙхQфИфИЊчЁЎхЎчцчЉЗшЊхЈцКяМDFAхQMцЏфИфИЊфКх чЛхQM=хQKхQ?#931;хQfхQSхQZхQх ЖфИ?br />уу① KцЏфИфИЊцНIЗщхQхЎчцЏфИЊх чД чЇАфИоZИфИЊчЖцяМ
уу② ΣцЏфИфИЊцНIЗхцЏшЁЈхQхЎчцЏфИЊх чД чЇАфИоZИфИЊшОх ЅчЌІхјPМцфЛЅфЙПU?#931;фИјОх ЅчЌІхЗхцЏшЁЈхQ?br />уу③ fцЏш{цЂхНцЭМцЏK×Σ→KфИчц хАхQхГхQхІ fхQkiхQaхQ?kjхQяМki∈KхQkj∈KхQхАБцхГчхQ?br />хНхчЖцфиkiхQшОх ЅчЌІфИКaцгМЎш{цЂфифИфИфИЊчЖцkjхQцфЛЌцkjПUюCНkiчфИфИЊхОlЇчЖцяМ
уу④ S ∈ KцЏхЏфИчфИфИЊхцяМ
уу⑤ Z⊂KцЏфИфИЊчЛцщхQчЛцфЙПUАхЏцЅхчЖццОlцчЖцу?/span>
шЏЅщЂччЖцш{цЂхОхQ?br />
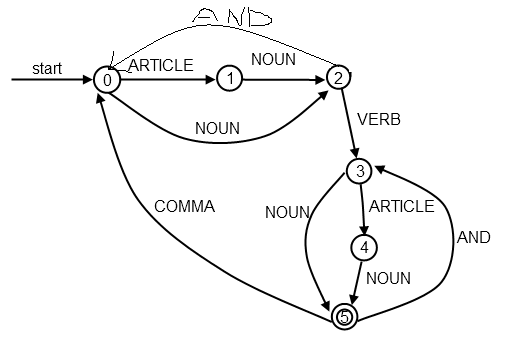
чАхЈхц ЙцЎчЖцш{цЂхОхQхфИфИЊцЈЁцш{цЂх ГОpШхw ЎБщхИИцЙфОПфКууу?br /> фЛЃч хІфИхQ?br />
#include <string>
#include <vector>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
string strNouns[8] =
{
"tom", "jerry", "goofy", "mickey",
"jimmy", "dog", "cat", "mouse"
};
bool IsNoun(string& str)
{
for (int i = 0; i < 8; ++i)
{
if (str == strNouns[i])
{
return true;
}
}
return false;
}
bool IsVerb(string& str)
{
return str == "hate" || str == "love"
|| str == "know" || str == "like"
|| str == "hates" || str == "loves"
|| str == "knows" || str == "likes";
}
bool IsArticle(string& str)
{
return str == "a" || str == "the";
}
bool CheckState(vector<string>& vs)
{
if (vs.empty()) return false;
int nState = 0;
for (int i = 0; i < vs.size(); ++i)
{
//printf("nState:%d, str:%s\n", nState, vs[i].c_str());
switch (nState)
{
case 0:
if (IsArticle(vs[i]))
{
nState = 1;
break;
}
else if (IsNoun(vs[i]))
{
nState = 2;
break;
}
else
{
return false;
}
case 1:
if (IsNoun(vs[i]))
{
nState = 2;
break;
}
else
{
return false;
}
case 2:
if (vs[i] == "and")
{
nState = 0;
break;
}
else if (IsVerb(vs[i]))
{
nState = 3;
break;
}
else
{
return false;
}
case 3:
if (IsArticle(vs[i]))
{
nState = 4;
break;
}
else if (IsNoun(vs[i]))
{
nState = 5;
break;
}
else
{
return false;
}
case 4:
if (IsNoun(vs[i]))
{
nState = 5;
break;
}
else
{
return false;
}
case 5:
if (vs[i] == "and")
{
nState = 3;
break;
}
else if (vs[i] == ",")
{
nState = 0;
break;
}
else
{
return false;
}
}
}
return nState == 5;
}
int main()
{
int nT;
scanf("%d%*c", &nT);
while (nT--)
{
vector<string> vs;
string line, str;
getline(cin, line);
stringstream ss(line);
while (ss >> str)
{
vs.push_back(str);
}
printf("%s\n", CheckState(vs) ? "YES I WILL" : "NO I WON'T");
}
return 0;
}
#include <vector>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
string strNouns[8] =
{
"tom", "jerry", "goofy", "mickey",
"jimmy", "dog", "cat", "mouse"
};
bool IsNoun(string& str)
{
for (int i = 0; i < 8; ++i)
{
if (str == strNouns[i])
{
return true;
}
}
return false;
}
bool IsVerb(string& str)
{
return str == "hate" || str == "love"
|| str == "know" || str == "like"
|| str == "hates" || str == "loves"
|| str == "knows" || str == "likes";
}
bool IsArticle(string& str)
{
return str == "a" || str == "the";
}
bool CheckState(vector<string>& vs)
{
if (vs.empty()) return false;
int nState = 0;
for (int i = 0; i < vs.size(); ++i)
{
//printf("nState:%d, str:%s\n", nState, vs[i].c_str());
switch (nState)
{
case 0:
if (IsArticle(vs[i]))
{
nState = 1;
break;
}
else if (IsNoun(vs[i]))
{
nState = 2;
break;
}
else
{
return false;
}
case 1:
if (IsNoun(vs[i]))
{
nState = 2;
break;
}
else
{
return false;
}
case 2:
if (vs[i] == "and")
{
nState = 0;
break;
}
else if (IsVerb(vs[i]))
{
nState = 3;
break;
}
else
{
return false;
}
case 3:
if (IsArticle(vs[i]))
{
nState = 4;
break;
}
else if (IsNoun(vs[i]))
{
nState = 5;
break;
}
else
{
return false;
}
case 4:
if (IsNoun(vs[i]))
{
nState = 5;
break;
}
else
{
return false;
}
case 5:
if (vs[i] == "and")
{
nState = 3;
break;
}
else if (vs[i] == ",")
{
nState = 0;
break;
}
else
{
return false;
}
}
}
return nState == 5;
}
int main()
{
int nT;
scanf("%d%*c", &nT);
while (nT--)
{
vector<string> vs;
string line, str;
getline(cin, line);
stringstream ss(line);
while (ss >> str)
{
vs.push_back(str);
}
printf("%s\n", CheckState(vs) ? "YES I WILL" : "NO I WON'T");
}
return 0;
}
yx 2012-10-12 22:14 хшЁЈшЏшЎК
]]>