之前一直在做移動機(jī)器人定位算法。查來查去，發(fā)覺粒子濾波算法（又叫MC算法）應(yīng)該算是最流行的了。因此開始學(xué)習(xí)使用之。入手的是本英文書叫 “probalistic robotic” 很不錯，我所見到的講得最好的一本書。花了大量時間去研讀。在這里我想談?wù)勎覍αＷ訛V波的一點認(rèn)識。因為在這一領(lǐng)域算是個新手。希望有前輩或者達(dá)人來指正 我的想法。也希望我的這篇文章對新手有理解他有所幫助（當(dāng)初我就很是苦于它難于理解）在這里我不想談粒子濾波的理論基礎(chǔ)和推到，這點大家可以去自己翻書。 我只談下我的體會。
粒子濾波算法。他源于Montecarlo的思想，即以某事件出現(xiàn)的頻率來指代該事件的概率。因此在濾波過程中，需要用到概率如P(x)的地方，一 概對變量x采樣，以大量采樣的分布近似來表示P(x)。因此，采用此一思想，在濾波過程中粒子濾波可以處理任意形式的概率，而不像Kalman濾波只能處 理高斯分布的概率問題。他的一大優(yōu)勢也在于此。
再來看對任意如下的狀態(tài)方程
x(t)=f(x(t-1),u(t),w(t))
y(t)=h(x(t),e(t))
其中的x(t)為t時刻狀態(tài)，u(t)為控制量，w(t) 和e(t)分別為模型噪聲和，觀測噪聲。前一個當(dāng)然是狀態(tài)轉(zhuǎn)移方程，后一個是觀測方程。那么對于這么一個問題粒子濾波怎么來從觀測y(t)，和x(t-1),u(t) 濾出真實狀態(tài)x(t)呢？
看看濾波的預(yù)估階段：粒子濾波首先根據(jù)x(t-1) 和他的概率分布生成大量的采樣，這些采樣就稱之為粒子。那么這些采樣在狀態(tài)空間中的分布實際上就是x(t-1) 的概率分布了。好，接下來依據(jù)狀態(tài)轉(zhuǎn)移方程加上控制量可以對每一粒子得到一個預(yù)測粒子。所有的預(yù)測粒子就代表了涉及哪些參數(shù)化的東西）。
進(jìn)入校正階段來：有了預(yù)測粒子，當(dāng)然不是所有的預(yù)測粒子都能得到我們的時間觀測值y對不，越是接近真實狀態(tài)的粒子，當(dāng)然獲得越有可能獲得觀測值y對吧。于是我們對所有的粒子得有個評價了，這個評價就是一個條件概率P(y|xi ),直白的說，這個條件概率代表了假設(shè)真實狀態(tài)x(t)取第i個粒子xi 時獲得觀測y的概率。令這個條件概率為第i個粒子的權(quán)重。如此這般下來，對所有粒子都進(jìn)行這么一個評價，那么越有可能獲得觀測y的粒子，當(dāng)然獲得的權(quán)重越高。好了預(yù)測信息融合在粒子的分布中，觀測信息又融合在了每一粒子的權(quán)重中。
哈哈最后采用重采樣算法（不知道什么是重采樣算法，那就只好翻書去吧），去除低權(quán)值的粒子，復(fù)制高權(quán)值的粒子。所得到的當(dāng)然就是我們說需要的真實狀態(tài)x(t)了，而這些重采樣后的粒子，就代表了真實狀態(tài)的概率分布了。
下一輪濾波，再將重采樣過后的粒子集輸入到狀態(tài)轉(zhuǎn)移方程中，直接就能夠獲得預(yù)測粒子了。。
初始狀態(tài)的問題： 咱們一開始對x(0)一無所知對吧，那咱們就認(rèn)為x(0)在全狀態(tài)空間內(nèi)平均分布唄。于是初始的采樣就平均分布在整個狀態(tài)空間中。然后將所有采樣輸入狀態(tài) 轉(zhuǎn)移方程，得到預(yù)測粒子。嘿嘿再評價下所有預(yù)測粒子的權(quán)重，當(dāng)然我們在整個狀態(tài)空間中只有部分粒子能夠獲的高權(quán)值咯。馬上重采樣算法來了，去除低權(quán)值的， 將下一輪濾波的考慮重點立馬縮小到了高權(quán)值粒子附近。哈哈就這么簡單。也很實用。
明白了沒？沒看糊涂吧哈哈。
如果大家看得還不過癮，后面有根據(jù)精彩的論述。
另外lishuai在文中也提到Particle filter的以下特點：
如果跟kalman濾波相比，那確實。畢竟kalman濾波可以直接得到狀態(tài)的解析估計，計算量很小。如果跟Markov定位相比，恰恰與 ricky所說相反，粒子濾波計算量小很多，而事實上，粒子濾波被用于定位的背景就是為了降低普通的Markov定位計算量相當(dāng)大并且隨著維數(shù)的增長計算 量迅速增長的缺陷。（Sebastian Thrun, Wolfram burgard, Dieter fox等在90年代做的一個圖書館機(jī)器人導(dǎo)航的項目，其中很多當(dāng)時他們的工作都成了現(xiàn)今機(jī)器人研究領(lǐng)域的熱點，比如粒子濾波，SLAM等）。
大家可能有幾個疑問，
1. Kalman濾波或者EKF都可以做定位并且運(yùn)算量小，為什么還要用什么Markov定位呢？
2. 為什么Markov定位計算量大并且隨著空間維數(shù)的增長而增長劇烈？
3.為什么粒子濾波這么神奇，讓計算量如此之大的Markov定位運(yùn)算量驟降？
4.到底粒子濾波實質(zhì)是什么？
好，現(xiàn)在就一一談一下我的看法
1. Kalman濾波或者EKF都可以做定位并且運(yùn)算量小，為什么還要用什么Markov定位呢？
燢alman濾波是有適用條件的，a。初始狀態(tài)必須是符合正態(tài)分布。b。必須是線性系統(tǒng)。（當(dāng)然，EKF通過將非線性系統(tǒng)線性化的方法處理非線性系統(tǒng)）。而真實的定位問題很多時候不滿足以上兩個條件。為什么不滿足呢？
先說為什么a不滿足：首先舉個正態(tài)分布無法描述的反例，大家都知道，正態(tài)分布是單峰函數(shù)，也就是說機(jī)器人初始時位于工作空間中某個位置的初始概 率最大，其他地方都比這小。如果是采用地圖匹配進(jìn)行絕對定位，上面描述的單峰高斯函數(shù)可能就無法精確的描述事實了，比如有十個一模一樣的房間。初始時把機(jī) 器人放在其中一個里面，機(jī)器人根據(jù)絕對測量傳感器獲得局部地圖，與他攜帶的先驗地圖匹配后他發(fā)現(xiàn)，他現(xiàn)在呆的位置在他的工作空間中有10個峰值，每個房間 一個，因為十個房間一模一樣，他無法區(qū)分。顯然，此時a假設(shè)不成立。
再說b為什么不滿足：這取決于真實機(jī)器人的物理特性，系統(tǒng)的狀態(tài)更新方程是由里程計或者是dead reckon 得到的，系統(tǒng)的觀測方程是由絕對定位系統(tǒng)（或者地圖匹配）得到的。對于一般的移動機(jī)器人，無論是兩個主動輪的形式還是一個主動輪一個steering wheel的形式，由此得到的狀態(tài)更新方程都是非線性的。
2. 為什么Markov定位計算量大并且隨著空間維數(shù)的增長而增長劇烈？
Markov定位的基本原理很簡單，就是用條件概率描述狀態(tài)更新，所有的可能的狀態(tài)都枚舉個遍，對于機(jī)器人的每一次更新，所有的可能的狀態(tài)遷移 都要被更新一遍，假設(shè)我們用柵格描述工作空間，假設(shè)t時刻機(jī)器人可能的位置為p1,p2,p3，在二維情況下采用正方形柵格劃分那么p1有8個鄰居，記為 p11，p12，p13，…,p18.在三維情況下，采用立方體劃分那么鄰居就更多了，有26個。如果維數(shù)繼續(xù)增加，那么鄰居增加的更厲害。這里我們以二 維情況為例來闡述問題。同理，我們記p2的鄰居為p21，p22，。。。p28。p3的鄰居為p31，p32，。。。，p38。在t時刻可能的位置只有3 個，然而t+1時刻，所有的三個的鄰居，以及p1，p2，p3都有可能成為當(dāng)前位置，但是根據(jù)dead reckon的結(jié)果，我們可以排除一些小概率的鄰居，減少計算量。但是隨著時間的推移，整個空間中的所有點都有可能成為估計的當(dāng)前位置（只不過各個位置的 概率不同而已）。這樣，如果不采取措施，那狀態(tài)的更新會是一件巨大的工程。并且，空間維數(shù)越大，節(jié)點數(shù)越多，計算量增長越厲害。
3.為什么粒子濾波這么神奇，讓計算量如此之大的Markov定位運(yùn)算量驟降？
粒子濾波強(qiáng)就強(qiáng)在它用統(tǒng)計的基于采樣的方法來描述整個空間中的概率分布。Markov的思想是你既然當(dāng)前位置的分布概率是個特殊分布，我就干脆 把你的樣本空間離散化（把空間劃分為柵格），計算每一個樣本的概率（計算每一個柵格的概率）。但是這帶來了問題2.為了解決這個問題，粒子濾波采用了另一 種思想：現(xiàn)在我不再均勻的把樣本空間離散化了，而是根據(jù)我當(dāng)前所掌握的概率分布對空間進(jìn)行采樣（重要性采樣），顯然，概率小的地方少采幾個樣(反正概率 小，即使采多了，每個樣本差別也不大，完全可以由附近的其他樣本反映）；概率高的地方應(yīng)該多采幾個樣。這樣，我們可以規(guī)定，每次都采樣N個，對于大概率的 地方多采，小概率的地方少采。根據(jù)概率里的大數(shù)定律，可以證明即使在維數(shù)增加的時候依然保持采N個樣，仍然可以保持性能。這就是粒子濾波高的地方，當(dāng)維數(shù) 非常高的情況，Markov定位都累的算不出來了，因為需要更新的狀態(tài)對實在是太多了，而人家粒子濾波依然只采N個樣，計算量還那樣，變化不大。
4.到底粒子濾波實質(zhì)是什么？
事實上，我們完全可以換一種思維來認(rèn)識粒子濾波。就是基于獎勵懲罰機(jī)制（強(qiáng)化學(xué)習(xí)）的優(yōu)化的思想。
首先，根據(jù)狀態(tài)轉(zhuǎn)移方程，對于每個粒子的位置進(jìn)行更新。但是這個更新只是基于dead reckon得到的，我們要融合絕對定位與相對定位，絕對定位的信息還沒有融合進(jìn)去呢。根據(jù)狀態(tài)轉(zhuǎn)移方程得到的新狀態(tài)到底行不行？能有多大的概率？這還取 決于絕對定位的結(jié)果也就是輸出方程。把狀態(tài)轉(zhuǎn)移方程的到的結(jié)果代入輸出方程，得到一個輸出，這個輸出是估計值，而根據(jù)絕對定位的觀測，這個值對應(yīng)的觀測值 也是可以測量得到的，現(xiàn)在這兩個值之間有個差額，很明顯，這個差額越小，剛才的到的狀態(tài)越可信，這個差額越大，狀態(tài)越不可信。好，就把這個指標(biāo)作為評估函 數(shù)（像GA，pso等優(yōu)化算法里的evaluation function),來修正各個狀態(tài)的估計概率。
總結(jié)一下，粒子濾波就是一種基于動態(tài)系統(tǒng)前向模型利用獎懲機(jī)制估計狀態(tài)值的一種方法。
轉(zhuǎn)自:http://blog.csdn.net/volkswageos/article/details/6508047
1. http://www.openslam.org/
2. http://www-personal.acfr.usyd.edu.au/nebot/victoria_park.htm 經(jīng)典數(shù)據(jù)庫
3. http://babel.isa.uma.es/mrpt/index.php/Main_Page 2008年開始陸續(xù)出現(xiàn)了一些好文章.
4. http://cres.usc.edu/radishrepository/view-all.php 包含了大量的用于驗證SLAM算法的數(shù)據(jù).
5. http://robots.stanford.edu/papers.html Standford 研究團(tuán)隊
6. http://www.isa.uma.es/C13/jlblanco/default.aspx 西班牙的一個博士生.編程能力極強(qiáng). 另外Jose Neira帶領(lǐng)的團(tuán)隊也比較猛.
7. http://cml.mit.edu/~jleonard/ 麻省理工的一個團(tuán)隊，參加了DARPA的智能車挑戰(zhàn)賽。目前主要從事水下SLAM的研究。
另外現(xiàn)在的利用飛機(jī)采集數(shù)據(jù)，研究SLAM是目前的一個熱點。最近幾年，理論上的突破已經(jīng)很有限。大量研究者開始轉(zhuǎn)向視覺SLAM。
代表人物牛津大學(xué)的Andrew Davison （http://www.doc.ic.ac.uk/~ajd/）
幾個牛人：
1. Tim Beily 及所在的 悉尼大學(xué)一些研究者
2.Giorgio Grisetti; Cyrill Stachniss; Wolfram Burgard; (GridMapping 算法,及概率機(jī)器人一書作者)
3. ;M. Montemerlo; Dirk Haehnel; Sebastian Thrun; (FastSLAM創(chuàng)始者,理論水平和實際應(yīng)用能力非常強(qiáng))。參加過DARPA的智能車挑戰(zhàn)賽，取得最好成績。
4. Austin Eliazar; Ronald Parr; (DP-SLAM創(chuàng)始者,從文章到數(shù)據(jù),程序都公開的牛人)
http://www.cs.duke.edu/~eliazar
http://www.cs.duke.edu/~parr
5. 以 Jose Neira和Jose luis Blanco為代表的一批西班牙學(xué)者.
6. Andrew Davison 視覺SLAM 領(lǐng)域的權(quán)威。
7.John Leonard 側(cè)重于 應(yīng)用。目前主要在做水下SLAM的項目。參加過DARPA的智能車挑戰(zhàn)賽。
http://cml.mit.edu/~jleonard
轉(zhuǎn)自：http://www.cnblogs.com/feisky/archive/2009/11/09/1599301.html
輸入圖像:
輸出圖像:
果1new.jpg)
源代碼:
(參考Matlab houghlines 例程)
clear
I = imread('taj1small3.jpg');
I = rgb2gray(I);
%I = imrotate(I,33,'crop');
% figure
% imshow(rotI);
figure
imshow(I);
BW = edge(I,'canny');
figure
imshow(BW);
[H,T,R] = hough(BW);
figure
imshow(H,[],'XData',T,'YData',R,
'InitialMagnification','fit');
xlabel('\theta'), ylabel('\rho');
axis on
axis normal
hold on
P = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
x = T(P(:,2)); y = R(P(:,1));
plot(x,y,'s','color','white');
% Find lines and plot them
lines = houghlines(BW,T,R,P,'FillGap',5,'MinLength',7);
figure, imshow(I),hold on
max_len = 0;
for k = 1:length(lines)
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
% Plot beginnings and ends of lines
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
% Determine the endpoints of the longest line segment
len = norm(lines(k).point1 - lines(k).point2);
if ( len > max_len)
max_len = len;
xy_long = xy;
end
end
% highlight the longest line segment
plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','blue');
PS: Matlab的例程寫的還真不錯,以后應(yīng)該多參考下...
前言：
上一次寫了關(guān)于PCA與LDA的文章，PCA的實現(xiàn)一般有兩種，一種是用特征值分解去實現(xiàn)的，一種是用奇異值分解去實現(xiàn)的。在上篇文章中便是基于特征值分解的一種解釋。特征值和奇異值在大部分人的印象中，往往是停留在純粹的數(shù)學(xué)計算中。而且線性代數(shù)或者矩陣論里面，也很少講任何跟特征值與奇異值有關(guān)的應(yīng)用背景。奇異值分解是一個有著很明顯的物理意義的一種方法，它可以將一個比較復(fù)雜的矩陣用更小更簡單的幾個子矩陣的相乘來表示，這些小矩陣描述的是矩陣的重要的特性。就像是描述一個人一樣，給別人描述說這個人長得濃眉大眼，方臉，絡(luò)腮胡，而且?guī)€黑框的眼鏡，這樣寥寥的幾個特征，就讓別人腦海里面就有一個較為清楚的認(rèn)識，實際上，人臉上的特征是有著無數(shù)種的，之所以能這么描述，是因為人天生就有著非常好的抽取重要特征的能力，讓機(jī)器學(xué)會抽取重要的特征，SVD是一個重要的方法。
在機(jī)器學(xué)習(xí)領(lǐng)域，有相當(dāng)多的應(yīng)用與奇異值都可以扯上關(guān)系，比如做feature reduction的PCA，做數(shù)據(jù)壓縮（以圖像壓縮為代表）的算法，還有做搜索引擎語義層次檢索的LSI（Latent Semantic Indexing）
另外在這里抱怨一下，之前在百度里面搜索過SVD，出來的結(jié)果都是俄羅斯的一種狙擊槍（AK47同時代的），是因為穿越火線這個游戲里面有一把狙擊槍叫做SVD，而在Google上面搜索的時候，出來的都是奇異值分解（英文資料為主）。想玩玩戰(zhàn)爭游戲，玩玩COD不是非常好嗎，玩山寨的CS有神馬意思啊。國內(nèi)的網(wǎng)頁中的話語權(quán)也被這些沒有太多營養(yǎng)的帖子所占據(jù)。真心希望國內(nèi)的氣氛能夠更濃一點，搞游戲的人真正是喜歡制作游戲，搞Data Mining的人是真正喜歡挖數(shù)據(jù)的，都不是僅僅為了混口飯吃，這樣談超越別人才有意義，中文文章中，能踏踏實實談?wù)劶夹g(shù)的太少了，改變這個狀況，從我自己做起吧。
前面說了這么多，本文主要關(guān)注奇異值的一些特性，另外還會稍稍提及奇異值的計算，不過本文不準(zhǔn)備在如何計算奇異值上展開太多。另外，本文里面有部分不算太深的線性代數(shù)的知識，如果完全忘記了線性代數(shù)，看本文可能會有些困難。
一、奇異值與特征值基礎(chǔ)知識：
特征值分解和奇異值分解在機(jī)器學(xué)習(xí)領(lǐng)域都是屬于滿地可見的方法。兩者有著很緊密的關(guān)系，我在接下來會談到，特征值分解和奇異值分解的目的都是一樣，就是提取出一個矩陣最重要的特征。先談?wù)勌卣髦捣纸獍桑?/p>
1）特征值：
如果說一個向量v是方陣A的特征向量，將一定可以表示成下面的形式：
這時候λ就被稱為特征向量v對應(yīng)的特征值，一個矩陣的一組特征向量是一組正交向量。特征值分解是將一個矩陣分解成下面的形式：
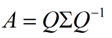
其中Q是這個矩陣A的特征向量組成的矩陣，Σ是一個對角陣，每一個對角線上的元素就是一個特征值。我這里引用了一些參考文獻(xiàn)中的內(nèi)容來說明一下。首先，要明確的是，一個矩陣其實就是一個線性變換，因為一個矩陣乘以一個向量后得到的向量，其實就相當(dāng)于將這個向量進(jìn)行了線性變換。比如說下面的一個矩陣：
它其實對應(yīng)的線性變換是下面的形式：
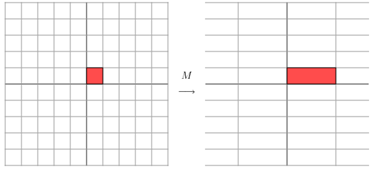
因為這個矩陣M乘以一個向量(x,y)的結(jié)果是：
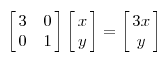上面的矩陣是對稱的，所以這個變換是一個對x，y軸的方向一個拉伸變換（每一個對角線上的元素將會對一個維度進(jìn)行拉伸變換，當(dāng)值>1時，是拉長，當(dāng)值<1時時縮短），當(dāng)矩陣不是對稱的時候，假如說矩陣是下面的樣子：
它所描述的變換是下面的樣子：
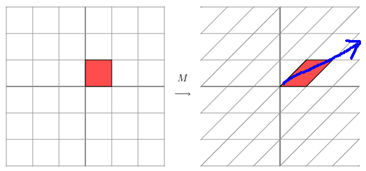
這其實是在平面上對一個軸進(jìn)行的拉伸變換（如藍(lán)色的箭頭所示），在圖中，藍(lán)色的箭頭是一個最主要的變化方向（變化方向可能有不止一個），如果我們想要描述好一個變換，那我們就描述好這個變換主要的變化方向就好了。反過頭來看看之前特征值分解的式子，分解得到的Σ矩陣是一個對角陣，里面的特征值是由大到小排列的，這些特征值所對應(yīng)的特征向量就是描述這個矩陣變化方向（從主要的變化到次要的變化排列）
當(dāng)矩陣是高維的情況下，那么這個矩陣就是高維空間下的一個線性變換，這個線性變化可能沒法通過圖片來表示，但是可以想象，這個變換也同樣有很多的變換方向，我們通過特征值分解得到的前N個特征向量，那么就對應(yīng)了這個矩陣最主要的N個變化方向。我們利用這前N個變化方向，就可以近似這個矩陣（變換）。也就是之前說的：提取這個矩陣最重要的特征。總結(jié)一下，特征值分解可以得到特征值與特征向量，特征值表示的是這個特征到底有多重要，而特征向量表示這個特征是什么，可以將每一個特征向量理解為一個線性的子空間，我們可以利用這些線性的子空間干很多的事情。不過，特征值分解也有很多的局限，比如說變換的矩陣必須是方陣。
（說了這么多特征值變換，不知道有沒有說清楚，請各位多提提意見。）
2）奇異值：
下面談?wù)勂娈愔捣纸狻Ｌ卣髦捣纸馐且粋€提取矩陣特征很不錯的方法，但是它只是對方陣而言的，在現(xiàn)實的世界中，我們看到的大部分矩陣都不是方陣，比如說有N個學(xué)生，每個學(xué)生有M科成績，這樣形成的一個N * M的矩陣就不可能是方陣，我們怎樣才能描述這樣普通的矩陣呢的重要特征呢？奇異值分解可以用來干這個事情，奇異值分解是一個能適用于任意的矩陣的一種分解的方法：
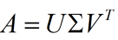假設(shè)A是一個N * M的矩陣，那么得到的U是一個N * N的方陣（里面的向量是正交的，U里面的向量稱為左奇異向量），Σ是一個N * M的矩陣（除了對角線的元素都是0，對角線上的元素稱為奇異值），V’(V的轉(zhuǎn)置)是一個N * N的矩陣，里面的向量也是正交的，V里面的向量稱為右奇異向量），從圖片來反映幾個相乘的矩陣的大小可得下面的圖片
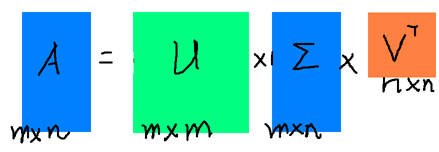
那么奇異值和特征值是怎么對應(yīng)起來的呢？首先，我們將一個矩陣A的轉(zhuǎn)置 * A，將會得到一個方陣，我們用這個方陣求特征值可以得到：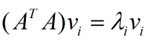
這里得到的v，就是我們上面的右奇異向量。此外我們還可以得到：
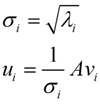這里的σ就是上面說的奇異值，u就是上面說的左奇異向量。奇異值σ跟特征值類似，在矩陣Σ中也是從大到小排列，而且σ的減少特別的快，在很多情況下，前10%甚至1%的奇異值的和就占了全部的奇異值之和的99%以上了。也就是說，我們也可以用前r大的奇異值來近似描述矩陣，這里定義一下部分奇異值分解：
r是一個遠(yuǎn)小于m、n的數(shù)，這樣矩陣的乘法看起來像是下面的樣子：
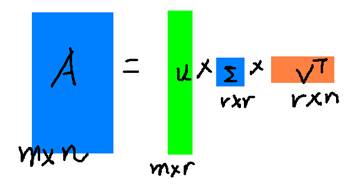
右邊的三個矩陣相乘的結(jié)果將會是一個接近于A的矩陣，在這兒，r越接近于n，則相乘的結(jié)果越接近于A。而這三個矩陣的面積之和（在存儲觀點來說，矩陣面積越小，存儲量就越小）要遠(yuǎn)遠(yuǎn)小于原始的矩陣A，我們?nèi)绻胍獕嚎s空間來表示原矩陣A，我們存下這里的三個矩陣：U、Σ、V就好了。
二、奇異值的計算：
奇異值的計算是一個難題，是一個O(N^3)的算法。在單機(jī)的情況下當(dāng)然是沒問題的，matlab在一秒鐘內(nèi)就可以算出1000 * 1000的矩陣的所有奇異值，但是當(dāng)矩陣的規(guī)模增長的時候，計算的復(fù)雜度呈3次方增長，就需要并行計算參與了。Google的吳軍老師在數(shù)學(xué)之美系列談到SVD的時候，說起Google實現(xiàn)了SVD的并行化算法，說這是對人類的一個貢獻(xiàn)，但是也沒有給出具體的計算規(guī)模，也沒有給出太多有價值的信息。
其實SVD還是可以用并行的方式去實現(xiàn)的，在解大規(guī)模的矩陣的時候，一般使用迭代的方法，當(dāng)矩陣的規(guī)模很大（比如說上億）的時候，迭代的次數(shù)也可能會上億次，如果使用Map-Reduce框架去解，則每次Map-Reduce完成的時候，都會涉及到寫文件、讀文件的操作。個人猜測Google云計算體系中除了Map-Reduce以外應(yīng)該還有類似于MPI的計算模型，也就是節(jié)點之間是保持通信，數(shù)據(jù)是常駐在內(nèi)存中的，這種計算模型比Map-Reduce在解決迭代次數(shù)非常多的時候，要快了很多倍。
Lanczos迭代就是一種解對稱方陣部分特征值的方法（之前談到了，解A’* A得到的對稱方陣的特征值就是解A的右奇異向量），是將一個對稱的方程化為一個三對角矩陣再進(jìn)行求解。按網(wǎng)上的一些文獻(xiàn)來看，Google應(yīng)該是用這種方法去做的奇異值分解的。請見Wikipedia上面的一些引用的論文，如果理解了那些論文，也“幾乎”可以做出一個SVD了。
由于奇異值的計算是一個很枯燥，純數(shù)學(xué)的過程，而且前人的研究成果（論文中）幾乎已經(jīng)把整個程序的流程圖給出來了。更多的關(guān)于奇異值計算的部分，將在后面的參考文獻(xiàn)中給出，這里不再深入，我還是focus在奇異值的應(yīng)用中去。
三、奇異值與主成分分析（PCA）：
主成分分析在上一節(jié)里面也講了一些，這里主要談?wù)勅绾斡肧VD去解PCA的問題。PCA的問題其實是一個基的變換，使得變換后的數(shù)據(jù)有著最大的方差。方差的大小描述的是一個變量的信息量，我們在講一個東西的穩(wěn)定性的時候，往往說要減小方差，如果一個模型的方差很大，那就說明模型不穩(wěn)定了。但是對于我們用于機(jī)器學(xué)習(xí)的數(shù)據(jù)（主要是訓(xùn)練數(shù)據(jù)），方差大才有意義，不然輸入的數(shù)據(jù)都是同一個點，那方差就為0了，這樣輸入的多個數(shù)據(jù)就等同于一個數(shù)據(jù)了。以下面這張圖為例子：
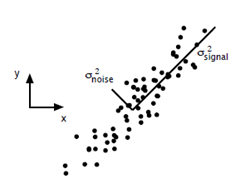這個假設(shè)是一個攝像機(jī)采集一個物體運(yùn)動得到的圖片，上面的點表示物體運(yùn)動的位置，假如我們想要用一條直線去擬合這些點，那我們會選擇什么方向的線呢？當(dāng)然是圖上標(biāo)有signal的那條線。如果我們把這些點單純的投影到x軸或者y軸上，最后在x軸與y軸上得到的方差是相似的（因為這些點的趨勢是在45度左右的方向，所以投影到x軸或者y軸上都是類似的），如果我們使用原來的xy坐標(biāo)系去看這些點，容易看不出來這些點真正的方向是什么。但是如果我們進(jìn)行坐標(biāo)系的變化，橫軸變成了signal的方向，縱軸變成了noise的方向，則就很容易發(fā)現(xiàn)什么方向的方差大，什么方向的方差小了。
一般來說，方差大的方向是信號的方向，方差小的方向是噪聲的方向，我們在數(shù)據(jù)挖掘中或者數(shù)字信號處理中，往往要提高信號與噪聲的比例，也就是信噪比。對上圖來說，如果我們只保留signal方向的數(shù)據(jù)，也可以對原數(shù)據(jù)進(jìn)行不錯的近似了。
PCA的全部工作簡單點說，就是對原始的空間中順序地找一組相互正交的坐標(biāo)軸，第一個軸是使得方差最大的，第二個軸是在與第一個軸正交的平面中使得方差最大的，第三個軸是在與第1、2個軸正交的平面中方差最大的，這樣假設(shè)在N維空間中，我們可以找到N個這樣的坐標(biāo)軸，我們?nèi)∏皉個去近似這個空間，這樣就從一個N維的空間壓縮到r維的空間了，但是我們選擇的r個坐標(biāo)軸能夠使得空間的壓縮使得數(shù)據(jù)的損失最小。
還是假設(shè)我們矩陣每一行表示一個樣本，每一列表示一個feature，用矩陣的語言來表示，將一個m * n的矩陣A的進(jìn)行坐標(biāo)軸的變化，P就是一個變換的矩陣從一個N維的空間變換到另一個N維的空間，在空間中就會進(jìn)行一些類似于旋轉(zhuǎn)、拉伸的變化。
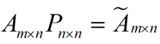
而將一個m * n的矩陣A變換成一個m * r的矩陣，這樣就會使得本來有n個feature的，變成了有r個feature了（r < n)，這r個其實就是對n個feature的一種提煉，我們就把這個稱為feature的壓縮。用數(shù)學(xué)語言表示就是：
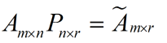但是這個怎么和SVD扯上關(guān)系呢？之前談到，SVD得出的奇異向量也是從奇異值由大到小排列的，按PCA的觀點來看，就是方差最大的坐標(biāo)軸就是第一個奇異向量，方差次大的坐標(biāo)軸就是第二個奇異向量…我們回憶一下之前得到的SVD式子：
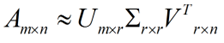在矩陣的兩邊同時乘上一個矩陣V，由于V是一個正交的矩陣，所以V轉(zhuǎn)置乘以V得到單位陣I，所以可以化成后面的式子
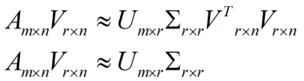將后面的式子與A * P那個m * n的矩陣變換為m * r的矩陣的式子對照看看，在這里，其實V就是P，也就是一個變化的向量。這里是將一個m * n 的矩陣壓縮到一個m * r的矩陣，也就是對列進(jìn)行壓縮，如果我們想對行進(jìn)行壓縮（在PCA的觀點下，對行進(jìn)行壓縮可以理解為，將一些相似的sample合并在一起，或者將一些沒有太大價值的sample去掉）怎么辦呢？同樣我們寫出一個通用的行壓縮例子：
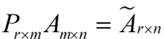這樣就從一個m行的矩陣壓縮到一個r行的矩陣了，對SVD來說也是一樣的，我們對SVD分解的式子兩邊乘以U的轉(zhuǎn)置U'
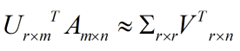這樣我們就得到了對行進(jìn)行壓縮的式子。可以看出，其實PCA幾乎可以說是對SVD的一個包裝，如果我們實現(xiàn)了SVD，那也就實現(xiàn)了PCA了，而且更好的地方是，有了SVD，我們就可以得到兩個方向的PCA，如果我們對A’A進(jìn)行特征值的分解，只能得到一個方向的PCA。
四、奇異值與潛在語義索引LSI：
潛在語義索引（Latent Semantic Indexing）與PCA不太一樣，至少不是實現(xiàn)了SVD就可以直接用的，不過LSI也是一個嚴(yán)重依賴于SVD的算法，之前吳軍老師在矩陣計算與文本處理中的分類問題中談到：
“三個矩陣有非常清楚的物理含義。第一個矩陣X中的每一行表示意思相關(guān)的一類詞，其中的每個非零元素表示這類詞中每個詞的重要性（或者說相關(guān)性），數(shù)值越大越相關(guān)。最后一個矩陣Y中的每一列表示同一主題一類文章，其中每個元素表示這類文章中每篇文章的相關(guān)性。中間的矩陣則表示類詞和文章雷之間的相關(guān)性。因此，我們只要對關(guān)聯(lián)矩陣A進(jìn)行一次奇異值分解，w 我們就可以同時完成了近義詞分類和文章的分類。（同時得到每類文章和每類詞的相關(guān)性）。”
上面這段話可能不太容易理解，不過這就是LSI的精髓內(nèi)容，我下面舉一個例子來說明一下，下面的例子來自LSA tutorial，具體的網(wǎng)址我將在最后的引用中給出：
這就是一個矩陣，不過不太一樣的是，這里的一行表示一個詞在哪些title中出現(xiàn)了（一行就是之前說的一維feature），一列表示一個title中有哪些詞，（這個矩陣其實是我們之前說的那種一行是一個sample的形式的一種轉(zhuǎn)置，這個會使得我們的左右奇異向量的意義產(chǎn)生變化，但是不會影響我們計算的過程）。比如說T1這個title中就有g(shù)uide、investing、market、stock四個詞，各出現(xiàn)了一次，我們將這個矩陣進(jìn)行SVD，得到下面的矩陣：
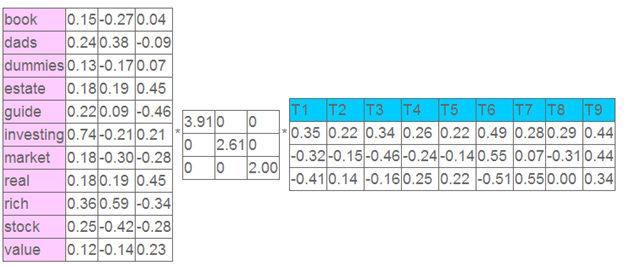左奇異向量表示詞的一些特性，右奇異向量表示文檔的一些特性，中間的奇異值矩陣表示左奇異向量的一行與右奇異向量的一列的重要程序，數(shù)字越大越重要。
繼續(xù)看這個矩陣還可以發(fā)現(xiàn)一些有意思的東西，首先，左奇異向量的第一列表示每一個詞的出現(xiàn)頻繁程度，雖然不是線性的，但是可以認(rèn)為是一個大概的描述，比如book是0.15對應(yīng)文檔中出現(xiàn)的2次，investing是0.74對應(yīng)了文檔中出現(xiàn)了9次，rich是0.36對應(yīng)文檔中出現(xiàn)了3次；
其次，右奇異向量中一的第一行表示每一篇文檔中的出現(xiàn)詞的個數(shù)的近似，比如說，T6是0.49，出現(xiàn)了5個詞，T2是0.22，出現(xiàn)了2個詞。
然后我們反過頭來看，我們可以將左奇異向量和右奇異向量都取后2維（之前是3維的矩陣），投影到一個平面上，可以得到：
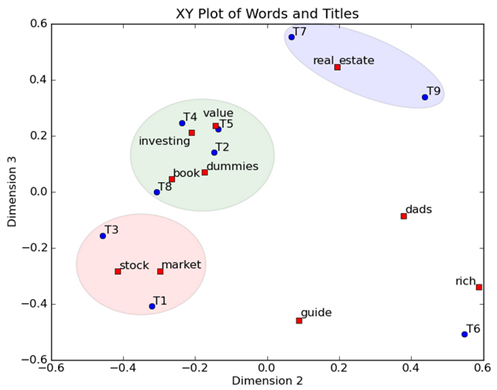在圖上，每一個紅色的點，都表示一個詞，每一個藍(lán)色的點，都表示一篇文檔，這樣我們可以對這些詞和文檔進(jìn)行聚類，比如說stock 和 market可以放在一類，因為他們老是出現(xiàn)在一起，real和estate可以放在一類，dads，guide這種詞就看起來有點孤立了，我們就不對他們進(jìn)行合并了。按這樣聚類出現(xiàn)的效果，可以提取文檔集合中的近義詞，這樣當(dāng)用戶檢索文檔的時候，是用語義級別（近義詞集合）去檢索了，而不是之前的詞的級別。這樣一減少我們的檢索、存儲量，因為這樣壓縮的文檔集合和PCA是異曲同工的，二可以提高我們的用戶體驗，用戶輸入一個詞，我們可以在這個詞的近義詞的集合中去找，這是傳統(tǒng)的索引無法做到的。
不知道按這樣描述，再看看吳軍老師的文章，是不是對SVD更清楚了？:-D
參考資料：
1）A Tutorial on Principal Component Analysis, Jonathon Shlens
這是我關(guān)于用SVD去做PCA的主要參考資料
2）http://www.ams.org/samplings/feature-column/fcarc-svd
關(guān)于svd的一篇概念好文，我開頭的幾個圖就是從這兒截取的
3）http://www.puffinwarellc.com/index.php/news-and-articles/articles/30-singular-value-decomposition-tutorial.html
另一篇關(guān)于svd的入門好文
4）http://www.puffinwarellc.com/index.php/news-and-articles/articles/33-latent-semantic-analysis-tutorial.html
svd與LSI的好文，我后面LSI中例子就是來自此
5）http://www.miislita.com/information-retrieval-tutorial/svd-lsi-tutorial-1-understanding.html
另一篇svd與LSI的文章，也還是不錯，深一點，也比較長
6）Singular Value Decomposition and Principal Component Analysis, Rasmus Elsborg Madsen, Lars Kai Hansen and Ole Winther, 2004
跟1）里面的文章比較類似
轉(zhuǎn)自:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html