#
以前一直對(duì)樹(shù)狀數(shù)組這種結(jié)構(gòu)并不感冒，因?yàn)橛X(jué)得它能做到的事兒線段樹(shù)也可以很好的完成。而且線段樹(shù)應(yīng)用更加靈活，可以說(shuō)比樹(shù)狀數(shù)組的應(yīng)用范圍大很多。不過(guò)最近碰到兩道題，都可以用樹(shù)狀數(shù)組這種結(jié)構(gòu)很好的解決，代碼非常精簡(jiǎn)單，特別是在二維應(yīng)用的時(shí)候，用線段樹(shù)非常麻煩，如果不是必要的話，不應(yīng)當(dāng)菜用線段樹(shù)這種結(jié)構(gòu)，而應(yīng)用樹(shù)狀數(shù)組。稍微研究了下樹(shù)狀數(shù)組這種結(jié)構(gòu)，寫個(gè)總結(jié)吧。
樹(shù)狀數(shù)組它的每個(gè)元素并不像普通數(shù)組那樣只保存自己的值，而是保存了從它開(kāi)始前2^k個(gè)值的和(k為位置后面的二進(jìn)制的0的個(gè)數(shù)）你可以看下圖：
粉線色結(jié)點(diǎn)都只保持它自己的值，因?yàn)樗鼈兊亩M(jìn)制未尾0個(gè)數(shù)為0。綠色結(jié)點(diǎn)都保持了自己與它前一個(gè)值的和，藍(lán)色結(jié)點(diǎn)保存了四個(gè)結(jié)點(diǎn)的值的和。棕色結(jié)點(diǎn)保存了8個(gè)結(jié)點(diǎn)的值的和。說(shuō)了這么多，這種結(jié)構(gòu)有什么用？它有什么優(yōu)勢(shì)呢？
它的主要優(yōu)勢(shì)就是可以快速求一段的和，即將求一段和的復(fù)雜度降到logN級(jí)別的，但是它增了修改一個(gè)元素的復(fù)雜度，使修改一個(gè)元素的復(fù)雜度也是logN級(jí)別的，不難知道，如果一個(gè)應(yīng)用對(duì)于查詢很多，每次查詢都是一個(gè)區(qū)間的和，那么樹(shù)狀數(shù)組它的優(yōu)勢(shì)就很明顯了。
問(wèn)題一：怎么求一段元素的和？如果要求A[i –> j]，顯然如果能快速求A[1->i-1]和A[1->j]那么問(wèn)題就解決了。怎么快速轉(zhuǎn)化呢？
因?yàn)槊總€(gè)位置它都包含了一段的值，如果這一段值被加進(jìn)來(lái)后，可以快速跳到下一個(gè)值，再求。如求A[1->6]，那么知道6包括兩個(gè)元素的和，下一次再求4，發(fā)現(xiàn)4包括四個(gè)元素的和，那么這兩個(gè)和加進(jìn)來(lái)就是結(jié)果。怎么快速求6的下一個(gè)元素呢？這就需要求出它二制后的0的個(gè)數(shù)的2的次冪，再與6作差即可。如6=(0000 0110)2，所以2^1=2 ,6-2=4, 4=(0000 0100), 所以2^2=4，4-4=0，結(jié)束。
int sum(int n) {
int ret = 0;
while(n > 0) {
ret += ss[n];
n -= lowbit(n);
}
return ret;
}
問(wèn)題二：怎么快速求一個(gè)數(shù)二進(jìn)制后面0的個(gè)數(shù)的2次冪？位運(yùn)算。兩種方法：x&(-x)或x&(x^(x-1))，它們都利用了位運(yùn)算的特點(diǎn)，因?yàn)槲覀円蟮木褪菑牡臀坏降礁呶话延龅降牡谝粋€(gè)1保持不變，其余各位清0的一個(gè)操作！
inline int lowbit(int x) {
return x & (x ^ (x - 1));
}
問(wèn)題三：怎么快速修改一個(gè)元素的值？從上面的圖可以看到，修改一個(gè)元素的值，所有包含它的值的元素都會(huì)被修改。同樣，它的變化只與求和有一些不同，求和是往下走，而修改值是往上走！
void change(int i, int value) {
while(i <= N) {
ss[i] += value;
i += lowbit(i);
}
}
變形應(yīng)用：上面應(yīng)用都是修改一個(gè)元素的值，求一段元素的和。那么它還可以進(jìn)行什么樣的操作呢？修改一段元素都增加或減少一個(gè)定值，查詢一個(gè)元素的值！同樣是logN級(jí)別的。問(wèn)題是這樣轉(zhuǎn)化的：如果把a(bǔ)-b區(qū)間內(nèi)的元素都要增加v，那么實(shí)際就可以把a(bǔ)元素增加v, b+1減少v，那么查詢a元素的值呢？就是求sum(1->a)所有元素的和就行了！這樣操作是否是正確的？正確性很容易證明，自己在紙上畫(huà)畫(huà)就會(huì)明白了。
二維樹(shù)狀數(shù)組與一維的情況類似。它也可以進(jìn)行一段的操作，變形應(yīng)用也可以。要注意的問(wèn)題就是修改的值會(huì)變成四個(gè)角。
本文來(lái)自CSDN博客，轉(zhuǎn)載請(qǐng)標(biāo)明出處：http://blog.csdn.net/MasterLuo/archive/2009/12/25/5073784.aspx
| You are now registered to take the GRE Split exam in |
Nanjing. |
| Test Date: |
2010-04-08 |
|
Test Time: |
08:30 |
| |
|
|
|
|
| Confirmation No.: |
8850000000460565 |
|
Test Center: |
8513 |
You must arrive at least 30 minutes prior to the testing time to allow for the check-in process and orientation. You will need to bring your confirmation number and two forms of photo-bearing identification with you on the day of the exam; at least one form of primary ID is required. Acceptable forms of primary identification in China are passport, citizenship ID (provisional citizenship ID is not acceptable) or military ID. The test administrator may also ask you to present a secondary form of identification; Secondary forms of Identification are driver license, student ID or employee ID. Identification must meet ETS -GRE requirements or you will not be permitted to test. Additional information on identification requirements can be found on Page 10 of the GRE information Bulletin.
| |
|
| The test center in Nanjing is located at: |
| |
| |
Address: |
Nanjing Testing Center,National Education Examinations Authority,1/F North Door of Library, Nanjing University, #22 Hankou Road,Nanjing, Jiang Su Province,P. R. China南京市漢口路22號(hào) 南京大學(xué)圖書(shū)館北側(cè)門一樓 教育部考試中心南京考點(diǎn) (210093) |
| |
|
|
|
| |
Tel: |
025-83594869 |
Fax: |
025-83594869 |
好題啊，才發(fā)現(xiàn)用網(wǎng)絡(luò)流也能解這么有實(shí)際意義的問(wèn)題，說(shuō)不定以后再工程中真的能遇到呢。
網(wǎng)絡(luò)上的方法是用KM,不過(guò)個(gè)人比較喜歡用最小費(fèi)用，就是跑得慢了點(diǎn)。
一點(diǎn)教訓(xùn)吧：這個(gè)題里面總點(diǎn)數(shù)應(yīng)該是2500+50+2
最小的邊數(shù)應(yīng)該是 (2500*50+50+2500)*2,剛開(kāi)始沒(méi)有乘以2，結(jié)果猛RE.后來(lái)想到網(wǎng)絡(luò)流里是要建正反邊的，汗啊。
建圖的代碼如下：
int main()
{
int t ;
int i,j,k;
scanf("%d",&t);
while(t--)
{
len=0;
int tem;
scanf("%d%d",&m,&n);
for(i=0;i<n*m+m+2;i++)
adj[i]=NULL;
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
{
scanf("%d", &tem);
for (k = 0; k < m; k++)
insert(i,m+j*m+k,1,(k + 1) * tem);
}
int s=n*m+m;
int t=n*m+m+1;
for(i=0;i<m;i++)
insert(s,i,1,0);
for(i=m;i<n*m+m;i++)
insert(i,t,1,0);
printf("%.6lf\n",(double)mincostflow(t+1,s,t)/(double)m);
}
return 0;
}
最近在學(xué)校刊物《正行》上發(fā)表了一遍關(guān)于小人的文章，由于比較匆忙，投稿時(shí)沒(méi)有經(jīng)過(guò)仔細(xì)地史料考證，原文中提到趙高是服毒而死，這是不符合歷史史實(shí)的，實(shí)際上，趙高死于秦王子?jì)胫帧?br>趙高(前259─前207)
趙高,本為趙國(guó)貴族，后入秦為宦官(一說(shuō)趙高為“宦官”乃后世曲解），任中車府令，兼行符璽令事，「管事二十余年」。秦始皇死后，他與李斯合謀偽造詔書(shū)，逼秦始皇長(zhǎng)子扶蘇自殺，另立胡亥為帝，并自任郎中令。他在任期間獨(dú)攬大權(quán)，結(jié)黨營(yíng)私，征役更加繁重，行政更加苛暴。公元前207年又設(shè)計(jì)害死李斯，成為秦國(guó)丞相。第二年他迫二世自殺，另立子?jì)搿２痪帽蛔計(jì)霘⒌簦D夷三族。
蠻麻煩的一個(gè)題 但是說(shuō)白了 也就是一個(gè)類似最長(zhǎng)上升子序列的東西（可能跳轉(zhuǎn)的跨度大了些） 從底部往上逐層DP,每一層有兩個(gè)狀態(tài) 分別求之。小結(jié)一下吧 做了這么多動(dòng)態(tài)規(guī)劃題 我發(fā)現(xiàn) 動(dòng)態(tài)規(guī)劃的實(shí)質(zhì) 居然是窮舉 ，囧啊，或者更確切的來(lái)說(shuō)是 帶記憶化的窮舉！存儲(chǔ)加遞歸應(yīng)該還是欠妥的，因?yàn)楫吘褂辛俗顑?yōu)子結(jié)構(gòu)以后 后效狀態(tài)便消除了，而且也并沒(méi)有揭示出DP解法的全局性（如果用更宏觀的視角來(lái)看待它），即它在求得答案的同時(shí)，也獲得了其他更多的信息，這些信息不是冗余（redundant 恩GRE高頻詞），形象的說(shuō) 應(yīng)該是在DP之路上，為答案作出貢獻(xiàn)的朋友，如果我們換一個(gè)問(wèn)題，也許它們也就成了答案。
對(duì)了，補(bǔ)充一下，我覺(jué)得這個(gè)題最重要的地方在于，當(dāng)你找到了一塊板剛好能接住從左側(cè)下降的你時(shí)，你便不用再考慮更下層的板了，因?yàn)槟悴豢赡艽Γò澹?
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
#define INF 999999999
struct node
{
int x1;
int x2;
int h;
bool operator <(node other)
{
return h>other.h;
}
}a[1005];
int dp[1001][2];
int n,x,y,mh;
int main()
{
int t;
int i,j,k;
scanf("%d",&t);
for(k=1;k<=t;k++)
{
scanf("%d%d%d%d",&n,&x,&y,&mh);
for(i=1;i<=n;i++)
{
scanf("%d%d%d",&a[i].x1,&a[i].x2,&a[i].h);
dp[i][0]=dp[i][1]=INF;
}
dp[n+1][0]=dp[n+1][1]=0;
a[n+1].x1=-INF;
a[n+1].x2=INF;
sort(a+1,a+1+n);
for(i=n;i>=1;i--)
{
bool l=false;
bool r=false;
for(j=i+1;j<=n+1;j++)
{
if(a[i].h-a[j].h>mh)
break;
if(!l&&a[i].x1>=a[j].x1&&a[i].x1<=a[j].x2)
{
if(j==n+1) dp[i][0]=0;
else
{
dp[i][0]=min(dp[i][0],dp[j][0]+a[i].x1-a[j].x1);
dp[i][0]=min(dp[i][0],dp[j][1]+a[j].x2-a[i].x1);
l=true;
}
}
if(!r&&a[i].x2>=a[j].x1&&a[i].x2<=a[j].x2)
{
if(j==n+1) dp[i][1]=0;
else
{
dp[i][1]=min(dp[i][1],dp[j][0]+a[i].x2-a[j].x1);
dp[i][1]=min(dp[i][1],dp[j][1]+a[j].x2-a[i].x2);
r=true;
}
}
}
}
int res=0;
for(i=1;i<=n+1;i++)
{
if(a[i].x1<=x&&x<=a[i].x2&&y>=a[i].h)
{
res=min(x-a[i].x1+dp[i][0],a[i].x2-x+dp[i][1]);
break;
}
}
res+=y;
printf("%d\n",res);
}
return 0;
}
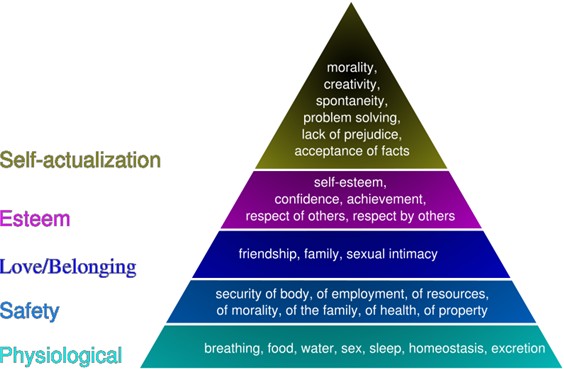
自我實(shí)現(xiàn)的需求
↑
尊重的需求（社會(huì)承認(rèn)的需求）
↑
社交的需求（社會(huì)關(guān)系的需求）
↑
安全的需求
↑
生理的需求（身體基本需求）
生理需要和安全需要得到滿足后，歸屬需要、自尊需要和自我實(shí)現(xiàn)的需要才能充分展現(xiàn)
1.生理需要是人類維持自身生存的最基本要求，它具有自我保存和種族延續(xù)的意義，在人類各種基本需要中占有最強(qiáng)的優(yōu)勢(shì)，也是人類社會(huì)發(fā)展的動(dòng)力。
（1）生理上的需要包括：
◆ 呼吸
◆ 水
◆ 食物
◆ 睡眠
◆ 生理平衡
◆ 分泌
◆ 性
如果這些需要（除性以外）任何一項(xiàng)得不到滿足，人類個(gè)人的生理機(jī)能就無(wú)法正常運(yùn)轉(zhuǎn)。換而言之，人類的生命就會(huì)因此受到威脅。在這個(gè)意義上說(shuō)，生理需要是推動(dòng)人們行動(dòng)最首要的動(dòng)力。馬斯洛認(rèn)為，只有這些最基本的需要滿足到維持生存所必需的程度后，其他的需要才能成為新的激勵(lì)因素，而到了此時(shí)，這些已相對(duì)滿足的需要也就不再成為激勵(lì)因素了。
2.安全需求是人們對(duì)于周圍環(huán)境的依賴和信賴。在現(xiàn)實(shí)中，安全需要常常是一個(gè)幻覺(jué)。即人們認(rèn)為有安全需要或沒(méi)有安全需要。
安全需求包括：
◆ 人身安全
◆ 健康保障
◆ 資源所有性
◆ 財(cái)產(chǎn)所有性
◆ 道德保障
◆ 工作職位保障
◆ 家庭安全
馬斯洛認(rèn)為，整個(gè)有機(jī)體是一個(gè)追求安全的機(jī)制，人的感受器官、效應(yīng)器官、智能和其他能量主要是尋求安全的工具，甚至可以把科學(xué)和人生觀都看成是滿足安全需要的一部分。當(dāng)然，當(dāng)這種需要一旦相對(duì)滿足后，也就不再成為激勵(lì)因素了。
3.歸屬需要就是參加和依附于一定組織的需要，愛(ài)的需要包括給予愛(ài)和接受愛(ài)，歸屬和愛(ài)的需要如果得不到滿足，個(gè)人就會(huì)感到孤獨(dú)和空虛。
包括
◆ 友情
◆ 愛(ài)情
◆ 性親密
人人都希望得到相互的關(guān)系和照顧。感情上的需要比生理上的需要來(lái)的細(xì)致，它和一個(gè)人的生理特性、經(jīng)歷、教育、宗教信仰都有關(guān)系。
4.尊重的需要包括兩個(gè)方面：自尊和他人對(duì)自己的尊重。這種需要的滿足會(huì)使人建立自信，使人覺(jué)得自己在這個(gè)世界上是有價(jià)值的、有能力的、有力量的。如果得不到滿足，就會(huì)導(dǎo)致自卑感、無(wú)助感和失落感。
◆ 自我尊重
◆ 信心
◆ 成就
◆ 對(duì)他人尊重
◆ 被他人尊重
人人都希望自己有穩(wěn)定的社會(huì)地位，要求個(gè)人的能力和成就得到社會(huì)的承認(rèn)。尊重的需要又可分為內(nèi)部尊重和外部尊重。內(nèi)部尊重就是人的自尊。外部尊重是指一個(gè)人希望有地位、有威信，受到別人的尊重、信賴和高度評(píng)價(jià)。馬斯洛認(rèn)為，尊重需要得到滿足，能使人對(duì)自己充滿信心，對(duì)社會(huì)滿腔熱情，體驗(yàn)到自己活著的用處和價(jià)值。
5.這種需要是一種創(chuàng)造、發(fā)揮個(gè)人潛能、實(shí)現(xiàn)自我理想、實(shí)現(xiàn)個(gè)人價(jià)值的需要。
◆ 道德
◆ 創(chuàng)造力
◆ 自覺(jué)性
◆ 問(wèn)題解決能力
◆ 公正度
◆ 接受現(xiàn)實(shí)能力
在馬斯洛看來(lái)，人類價(jià)值體系存在兩類不同的需要，一類是沿生物譜系上升方向逐漸變?nèi)醯谋灸芑驔_動(dòng)，稱為低級(jí)需要和生理需要。一類是隨生物進(jìn)化而逐漸顯現(xiàn)的潛能或需要，稱為高級(jí)需要。
人都潛藏著這五種不同層次的需要，但在不同的時(shí)期表現(xiàn)出來(lái)的各種需要的迫切程度是不同的。人的最迫切的需要才是激勵(lì)人行動(dòng)的主要原因和動(dòng)力。人的需要是從外部得來(lái)的滿足逐漸向內(nèi)在得到的滿足轉(zhuǎn)化。
低層次的需要基本得到滿足以后，它的激勵(lì)作用就會(huì)降低，其優(yōu)勢(shì)地位將不再保持下去，高層次的需要會(huì)取代它成為推動(dòng)行為的主要原因。有的需要一經(jīng)滿足，便不能成為激發(fā)人們行為的起因，于是被其他需要取而代之。
高層次的需要比低層次的需要具有更大的價(jià)值。熱情是由高層次的需要激發(fā)。人的最高需要即自我實(shí)現(xiàn)就是以最有效和最完整的方式表現(xiàn)他自己的潛力，惟此才能使人得到高峰體驗(yàn)。
摘要: 自己太水了。。。呵呵A題 打表。。。
#include<iostream>using namespace std;/**//*int dp[10000001];int rex[10000];int rey[10000];int main(){ freopen("out.txt",...
閱讀全文
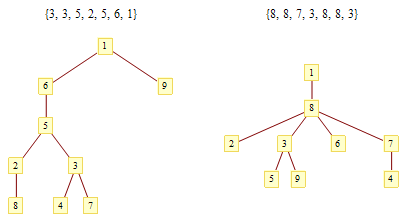
Cayley公式是說(shuō)，一個(gè)完全圖K_n有n^(n-2)棵生成樹(shù)，換句話說(shuō)n個(gè)節(jié)點(diǎn)的帶標(biāo)號(hào)的無(wú)根樹(shù)有n^(n-2)個(gè)。今天我學(xué)到了Cayley公式的一個(gè)非常簡(jiǎn)單的證明，證明依賴于Prüfer編碼，它是對(duì)帶標(biāo)號(hào)無(wú)根樹(shù)的一種編碼方式。
給定一棵帶標(biāo)號(hào)的無(wú)根樹(shù)，找出編號(hào)最小的葉子節(jié)點(diǎn)，寫下與它相鄰的節(jié)點(diǎn)的編號(hào)，然后刪掉這個(gè)葉子節(jié)點(diǎn)。反復(fù)執(zhí)行這個(gè)操作直到只剩兩個(gè)節(jié)點(diǎn)為止。由于節(jié)點(diǎn)數(shù)n>2的樹(shù)總存在葉子節(jié)點(diǎn)，因此一棵n個(gè)節(jié)點(diǎn)的無(wú)根樹(shù)唯一地對(duì)應(yīng)了一個(gè)長(zhǎng)度為n-2的數(shù)列，數(shù)列中的每個(gè)數(shù)都在1到n的范圍內(nèi)。下面我們只需要說(shuō)明，任何一個(gè)長(zhǎng)為n-2、取值范圍在1到n之間的數(shù)列都唯一地對(duì)應(yīng)了一棵n個(gè)節(jié)點(diǎn)的無(wú)根樹(shù)，這樣我們的帶標(biāo)號(hào)無(wú)根樹(shù)就和Prüfer編碼之間形成一一對(duì)應(yīng)的關(guān)系，Cayley公式便不證自明了。
注意到，如果一個(gè)節(jié)點(diǎn)A不是葉子節(jié)點(diǎn)，那么它至少有兩條邊；但在上述過(guò)程結(jié)束后，整個(gè)圖只剩下一條邊，因此節(jié)點(diǎn)A的至少一個(gè)相鄰節(jié)點(diǎn)被去掉過(guò)，節(jié)點(diǎn)A的編號(hào)將會(huì)在這棵樹(shù)對(duì)應(yīng)的Prüfer編碼中出現(xiàn)。反過(guò)來(lái)，在Prüfer編碼中出現(xiàn)過(guò)的數(shù)字顯然不可能是這棵樹(shù)（初始時(shí)）的葉子。于是我們看到，沒(méi)有在Prüfer編碼中出現(xiàn)過(guò)的數(shù)字恰好就是這棵樹(shù)（初始時(shí)）的葉子節(jié)點(diǎn)。找出沒(méi)有出現(xiàn)過(guò)的數(shù)字中最小的那一個(gè)（比如④），它就是與Prüfer編碼中第一個(gè)數(shù)所標(biāo)識(shí)的節(jié)點(diǎn)（比如③）相鄰的葉子。接下來(lái)，我們遞歸地考慮后面n-3位編碼（別忘了編碼總長(zhǎng)是n-2）：找出除④以外不在后n-3位編碼中的最小的數(shù)（左圖的例子中是⑦），將它連接到整個(gè)編碼的第2個(gè)數(shù)所對(duì)應(yīng)的節(jié)點(diǎn)上（例子中還是③）。再接下來(lái)，找出除④和⑦以外后n-4位編碼中最小的不被包含的數(shù)，做同樣的處理……依次把③⑧②⑤⑥與編碼中第3、4、5、6、7位所表示的節(jié)點(diǎn)相連。最后，我們還有①和⑨沒(méi)處理過(guò)，直接把它們倆連接起來(lái)就行了。由于沒(méi)處理過(guò)的節(jié)點(diǎn)數(shù)總比剩下的編碼長(zhǎng)度大2，因此我們總能找到一個(gè)最小的沒(méi)在剩余編碼中出現(xiàn)的數(shù)，算法總能進(jìn)行下去。這樣，任何一個(gè)Prüfer編碼都唯一地對(duì)應(yīng)了一棵無(wú)根樹(shù)，有多少個(gè)n-2位的Prüfer編碼就有多少個(gè)帶標(biāo)號(hào)的無(wú)根樹(shù)。
一個(gè)有趣的推廣是，n個(gè)節(jié)點(diǎn)的度依次為D1, D2, ..., Dn的無(wú)根樹(shù)共有(n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]個(gè)，因?yàn)榇藭r(shí)Prüfer編碼中的數(shù)字i恰好出現(xiàn)Di-1次。