Description
Write
a program that takes as input a rooted tree and a list of pairs of
vertices. For each pair (u,v) the program determines the closest common
ancestor of u and v in the tree. The closest common ancestor of two
nodes u and v is the node w that is an ancestor of both u and v and has
the greatest depth in the tree. A node can be its own ancestor (for
example in Figure 1 the ancestors of node 2 are 2 and 5)
Input
The data set, which is read from a the std input, starts with the tree description, in the form:
nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 ... successorn
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) ...
The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.
nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 ... successorn
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) ...
The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.
Output
For
each common ancestor the program prints the ancestor and the number of
pair for which it is an ancestor. The results are printed on the
standard output on separate lines, in to the ascending order of the
vertices, in the format: ancestor:times
For example, for the following tree:
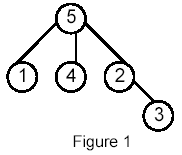
For example, for the following tree:
Sample Input
5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
(2 3)
(1 3) (4 3)
Sample Output
2:1
5:5
棰樻剰錛氱粰鍑烘爲鐨勭粨鏋勶紝鍐嶇粰鍑鴻璇㈤棶鐨勶紙u錛?v),姹傚嚭璇㈤棶鍚庡叕鍏辮妭鐐瑰嚭鐜扮殑涓暟銆?br>浠ｇ爜錛?br>#include <stdio.h>
#include <stdlib.h>
#include <vector>
#define maxn 1000
using namespace std;
int visit[maxn], in[maxn], f[maxn], anc[maxn], num[maxn];
vector<int> tree[maxn], que[maxn];
void set(int n)
{
for (int i = 1; i <= n; i++)
{
in[i] = 0;
visit[i] = 0;
num[i] = 0;
anc[i] = i;
f[i] = -1;
tree[i].clear();
que[i].clear();
}
}
int find(int a)
{
if (f[a] < 0)
{
return a;
}
return f[a] = find(f[a]);
}
void unions(int a, int b)
{
a = find(a);
b = find(b);
if (a != b)
{
if (f[a] > f[b])
{
f[b] += f[a];
f[a] = b;
}
else
{
f[a] += f[b];
f[b] = a;
}
}
}
void lca(int u)
{
int i, size;
size = tree[u].size();
for (i = 0; i < size; i++)
{
lca(tree[u][i]);
unions(u, tree[u][i]);
anc[find(u)] = u;
}
visit[u] = 1;
size = que[u].size();
for (i = 0; i < size; i++)
{
if (visit[que[u][i]] == 1)
{
num[anc[find(que[u][i])]]++;
}
}
}
int main()
{
char a[100], b[100];
int n, i, j, u, v, m;
while (scanf("%d", &n) != EOF)
{
set(n);
for (i = 0; i < n; i++)
{
scanf("%d:(%d)", &u, &m);
for (j = 0; j < m; j++)
{
scanf("%d", &v);
tree[u].push_back(v);
in[v]++;
}
}
scanf("%d", &m);
while (m--)
{
scanf(" (%d %d)", &u, &v);
que[u].push_back(v);
que[v].push_back(u);
}
for (i = 1; i <= n; i++)
{
if (in[i] == 0)
{
lca(i);
break;
}
}
for (i = 1; i <= n; i++)
{
if (num[i])
{
printf("%d:%d\n", i, num[i]);
}
}
}
system("pause");
return 0;
}
]]>
Description
Farmer
John's cows refused to run in his marathon since he chose a path much
too long for their leisurely lifestyle. He therefore wants to find a
path of a more reasonable length. The input to this problem consists of
the same input as in "Navigation Nightmare",followed by a line
containing a single integer K, followed by K "distance queries". Each
distance query is a line of input containing two integers, giving the
numbers of two farms between which FJ is interested in computing
distance (measured in the length of the roads along the path between
the two farms). Please answer FJ's distance queries as quickly as
possible!
Input
* Lines 1..1+M: Same format as "Navigation Nightmare"
* Line 2+M: A single integer, K. 1 <= K <= 10,000
* Lines 3+M..2+M+K: Each line corresponds to a distance query and contains the indices of two farms.
* Line 2+M: A single integer, K. 1 <= K <= 10,000
* Lines 3+M..2+M+K: Each line corresponds to a distance query and contains the indices of two farms.
Output
* Lines 1..K: For each distance query, output on a single line an integer giving the appropriate distance.
Sample Input
7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S
3
1 6
1 4
2 6
Sample Output
13
3
36
棰樻剰錛氱粰鍑轟竴媯墊爲錛屽叾瀹炴槸涓浘銆傛眰鍑轟袱鐐逛箣闂寸殑鏈鐭窛紱匯?br>#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define maxn 600010
int son[maxn], loc[maxn], dis[maxn], sw[maxn], indegree[maxn], th;
struct T
{
int e, d;
}rmq[maxn*2][30];
struct F
{
int u, v, w, next;
}fn[maxn * 2];
void set(int n)
{
for (int i = 1; i <= n; i++)
{
son[i] = 0;
indegree[i] = 0;
dis[i] = -1;
loc[i] = -1;
}
for (int i = 1; i <= n; i++)
{
fn[i].next = 0;
}
}
void link(int u, int v, int w)
{
/*
鏍戠殑閬嶅巻錛岃繖涓緱璁頒綇銆傝妭鐪佺┖闂淬?br> */
th++;
fn[th].u = u, fn[th].v = v, fn[th].w = w, fn[th].next = son[u], son[u] = th;
th++;
fn[th].u = v, fn[th].v = u, fn[th].w = w, fn[th].next = son[v], son[v] = th;
}
/*
閫氳繃鎼滅儲鏉ョ敓鎴愭爲鐨勯亶鍘嗚妭鐐?br>*/
void dfs(int d, int u, int f, int sd)
{
int v, i;
th++;
if (loc[u] == -1)//鍙繕娌″嚭鐜拌繃鐨勮妭鐐瑰湪閬嶅巻涓殑鏃墮棿鎴籌紙浣嶇疆錛?/span>
{
loc[u] = th;
dis[u] = sd;//璺濈鏄彔鍔犵殑銆?/span>
}
rmq[th][0].e = u;
rmq[th][0].d = d;
for (i = son[u]; i; i = fn[i].next)
{
if (fn[i].v != f)
{
dfs(d + 1, fn[i].v, u, sd + fn[i].w);
th++;
rmq[th][0].e = u;
rmq[th][0].d = d;
}
}
}
void build (int n)
{
int c = log((double)n) / log(2.0), i, j, m;
for (i = 1; i <= c; i++)
{
for (j = 1; j <= n; j++)
{
m = j + (1 << (i - 1));
if (m > n)
{
rmq[j][i] = rmq[j][i-1];
}
else
{
if (rmq[j][i-1].d <= rmq[m][i-1].d)
{
rmq[j][i] = rmq[j][i-1];
}
else
{
rmq[j][i] = rmq[m][i-1];
}
}
}
}
}
int query(int u, int v)
{
if (loc[u] > loc[v])
{
u ^= v;
v ^= u;
u ^= v;
}
int i = loc[u], j = loc[v];
int len = j - i + 1;
int c = log((double)len) / log(2.0);
int m = j - (1 << c) + 1;
int ancestor;
if (rmq[i][c].d <= rmq[m][c].d)
{
ancestor = rmq[i][c].e;
}
else
{
ancestor = rmq[m][c].e;
}
return dis[u] + dis[v] - 2 * dis[ancestor];
}
int main()
{
char c[2];
int n, m, u, v, w, k, t, i;
scanf("%d%d", &n, &m);
set(n);
th = 0;
while (m--)
{
scanf("%d%d%d%s", &u, &v, &w, c);
link(u, v, w);
}
th = 0;
dfs(0, 1, 0, 0);
build (2 * n - 1);
scanf("%d", &k);
while (k--)
{
scanf("%d%d", &u, &v);
printf("%d\n", query(u, v));
}
return 0;
}
]]>
Description
You are given a sequence of n integers a1 , a2 , ... , an in non-decreasing order. In addition to that, you are given several queries consisting of indices i and j (1 ≤ i ≤ j ≤ n). For each query, determine the most frequent value among the integers ai , ... , aj.
Input
The input consists of several test cases. Each test case starts with a line containing two integers n and q (1 ≤ n, q ≤ 100000). The next line contains n integers a1 , ... , an (-100000 ≤ ai ≤ 100000, for each i ∈ {1, ..., n}) separated by spaces. You can assume that for each i ∈ {1, ..., n-1}: ai ≤ ai+1. The following q lines contain one query each, consisting of two integers i and j (1 ≤ i ≤ j ≤ n), which indicate the boundary indices for the
query.
The last test case is followed by a line containing a single 0.
Output
For each query, print one line with one integer: The number of occurrences of the most frequent value within the given range.
Sample Input
10 3
-1 -1 1 1 1 1 3 10 10 10
2 3
1 10
5 10
0
Sample Output
1
4
3
棰樻剰錛氭煡鎵懼尯闂村唴鏁板嚭鐜版渶澶氱殑嬈℃暟
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define maxn 100010
#define Max(a, b) a > b ? a : b
int num[maxn], v[maxn], rq[maxn][20];
void build(int n)
{
int i, j, m, r = n, c = log((double)n) / log(2.0);
for (i = 1; i <= n; i++)
{
rq[i][0] = v[i];
}
for (i = 1; i <= c; i++)
{
for (j = 1; j <= r; j++)
{
m = j + (1 << (i - 1));a
if (m <= r)
{
rq[j][i] = Max(rq[j][i-1], rq[m][i-1]);
}
else
{
rq[j][i] = rq[j][i-1];
}
}
}
}
int rmq(int l, int r)
{
int len = r - l + 1;
int k = log(double(len)) / log(2.0);
int m = r - (1 << k) + 1;
return Max(rq[l][k], rq[m][k]);
}
int query(int l, int r)
{
int left, i;
if (num[l] == num[r])
{
return r - l + 1;
}
for (i = l; ; i++)
{
if (v[i] == 1)
{
left = i - l;
break;
}
}
return Max(left, rmq(i, r));
}
int main()
{
int n, m, i, l, r;
while (scanf("%d%d", &n, &m) == 2)
{
scanf("%d", &num[1]);
v[1] = 1;
for (i = 2; i <= n; i++)
{
scanf("%d", &num[i]);
if (num[i] == num[i-1])
{
v[i] = v[i-1] + 1;
}
else
{
v[i] = 1;
}
}
build(n);
while (m--)
{
scanf("%d%d", &l, &r);
printf("%d\n", query(l, r));
}
}
return 0;
}
]]>
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The
input consists of T test cases. The number of test cases (T) is given
in the first line of the input file. Each test case starts with a line
containing an integer N , the number of nodes in a tree,
2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N.
Each of the next N -1 lines contains a pair of integers that represent
an edge --the first integer is the parent node of the second integer.
Note that a tree with N nodes has exactly N - 1 edges. The last line of
each test case contains two distinct integers whose nearest common
ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
棰樻剰錛氱粰鍑烘爲鐨勭粨鏋勶紝闂袱鑺傜偣鐨勬渶榪戝叕鍏辯埗鑺傜偣銆?br>浠ｇ爜錛?br>#include <stdio.h>
#include <vector>
#define maxn 10001
using namespace std;
int visit[maxn], indegree[maxn], f[maxn], ancestor[maxn];
vector<int> tree[maxn], que[maxn];
void init(int n)
{
int i;
for (i = 1; i <= n; i++)
{
tree[i].clear();
que[i].clear();
f[i] = -1;
visit[i] = 0;
indegree[i] = 0;
ancestor[i] = i;
}
}
int find(int a)
{
if (f[a] < 0)
{
return a;
}
return f[a] = find(f[a]);
}
void unions(int a, int b)
{
a = find(a), b = find(b);
if (a != b)
{
if (f[a] > f[b])
{
f[b] += f[a];
f[a] = b;
}
else
{
f[a] += f[b];
f[b] = a;
}
}
}
void lca(int u)
{
int i, size;
size = tree[u].size();
for (i = 0; i < size; i++)
{
lca(tree[u][i]);
unions(u, tree[u][i]);
ancestor[find(u)] = u;
/*瀵逛簬澶勭悊榪囩殑瀛╁瓙錛屽叾紲栧厛瑕佹敼涓哄綋鍓嶈妭鐐癸紝淇濊瘉榪欐５鏁扮殑閬嶅巻閫昏緫錛?br> 鍥犱負騫舵煡闆嗙殑鍚堝茍鏄寜鏉冨艱岄潪閬嶅巻欏哄簭鍚堝茍鐨?閫氳繃騫舵煡闆嗛珮鏁堣幏寰楀瓙鏍戦泦鍚堢殑绔彛錛屽湪閫氳繃榪欑鍙ｈ幏寰?br> 璇ュ瓙鏍戝湪榪欎釜鏃墮棿孌電殑鐪熸鏈榪戠埗鑺傜偣錛屽鍥句腑鐨?鍦ㄥ茍鏌ユ爲涓細琚綊騫朵負6鐨勫瀛愶紝鍥犱負鏉冨肩殑闂*/
}
visit[u] = 1;
size = que[u].size();
for (i = 0; i < size; i++)
{
if (visit[que[u][i]] == 1)
{
printf("%d\n", ancestor[find(que[u][i])]);
return;
}
}
}
int main()
{
int n, t, i, u, v;
scanf("%d", &t);
while (t--)
{
scanf("%d", &n);
init(n);
for (i = 1; i < n; i++)
{
scanf("%d%d", &u, &v);
tree[u].push_back(v);
indegree[v]++;
}
scanf("%d%d", &u, &v);
que[u].push_back(v);
que[v].push_back(u);
for (i = 1; i <= n; i++)
{
if (indegree[i] == 0)
{
lca(i);
break;
}
}
}
return 0;
}
]]>
f[i][j]琛ㄧず浠涓鴻搗鐐歸暱搴︿負2^j鐨勬渶鍊箋?/span>
f[i][j] = rmq(f[i][j-1], f[i + 2 ^ (j-1)][j-1];鐩稿綋浜庢妸綰挎鍒嗘垚鐩哥瓑鐨勫乏鍙充袱孌靛悎騫舵眰rmq銆備絾榪欏緱璁╃嚎孌甸暱搴︽槸2鐨勫箓嬈°?/span>
鏌ヨ鏃訛紝渚嬪f[1錛?] = f[1][2] + f[5][1] + f[7][0];涓篛(logn),f[1, 7]瀵瑰簲浜庢暟緇勪腑鐨勫尯闂?/span>
涓轟簡鍔犲揩鏌ヨ錛屽彲浣縡[1錛?] = f[1][2] + f[4][2];涓篛(1)錛岃繖閲岀敤2=錛?^k <= 7錛塳鐨勬渶澶у? - 2^2 + 1 涓?錛屽嵆璁?鍚戝乏縐誨姩2^2 - 1涓綅錛?^k = 1 << k;娉ㄦ剰錛氫緥濡傜粰鍑簄=7錛屽垯f[4][2]鏄眰瀵瑰簲浜嶽4, 8]鐨剅mq錛岃宖[4, 8] = f[4, 7],鎵浠ヨ瀵規榪涜棰勫鐞?璁╁彸鍖洪棿鐨勫艱秴榪噉鐨勪負鍙沖尯闂翠負n鏃剁殑鍊鹼紝榪欐牱鎵嶈兘鍔犲揩鏌ヨ錛屽嵆澶氬鍔犱簡涓浜涙柟渚挎煡璇㈢殑鏁版嵁銆傛渶澶у乏縐繪槸k = log2(n),鍙〃紺虹殑鏈澶ц搗濮嬬偣鏄? << k,鍒檉[i][j]琛ㄧず鐨勫彸鍖洪棿鐨勬渶澶у間負
(1 << k) + (1 << k) = 1 << (k + 1) = 2 ^ (log2(n) + 1),鎻愪緵榪欎釜鏁版嵁鏃惰兘緇欏嚭浣曟椂寰楃┖闂碵n + 1][log2(n) + 1 + 1]銆?/span>
浠ｇ爜錛?/span>
#include
<
stdio.h
>
#include < stdlib.h >
#include < math.h >
#define maxn 50010
#define Min(a, b) a < b ? a : b
#define Max(a, b) a > b ? a : b
struct t
{
int min, max;
}map[maxn][ 20 ];
void build ( int n)
{
int i, j, m, r = n, c = log(( double )n) / log( 2.0 );
for (i = 1 ; i <= c; i ++ )
{
for (j = 1 ; j <= r; j ++ )
{
m = j + ( 1 << (i - 1 )); // 鍙沖崐閮ㄥ垎鐨勮搗濮嬪?/span>
if (m <= r)
{
map[j][i].min = Min(map[j][i - 1 ].min ,map[m][i - 1 ].min);
map[j][i].max = Max(map[j][i - 1 ].max, map[m][i - 1 ].max);
}
else // 闀垮害瓚呭嚭n鐨勶紝灝卞綋鏄痡璧風偣鐨勬渶鍚庝竴涓粓鐐圭殑rmq銆傚疄鐜拌繖姝ヨ兘浣挎煡璇負O(1).
{
map[j][i].min = map[j][i - 1 ].min;
map[j][i].max = map[j][i - 1 ].max;
}
}
}
}
int query( int l, int r)
{
int len = r - l + 1 ;
int k = log(( double )len) / log( 2.0 );
int m = r - ( 1 << k) + 1 ;
int min = Min(map[l][k].min, map[m][k].min);
int max = Max(map[l][k].max, map[m][k].max);
return max - min;
}
int main()
{
int n, m, i, l, r;
scanf( " %d%d " , & n, & m);
for (i = 1 ; i <= n; i ++ )
{
scanf( " %d " , & map[i][ 0 ].min);
map[i][ 0 ].max = map[i][ 0 ].min;
}
build (n);
while (m -- )
{
scanf( " %d%d " , & l, & r);
printf( " %d\n " , query(l, r));
}
return 0 ;
}
#include < stdlib.h >
#include < math.h >
#define maxn 50010
#define Min(a, b) a < b ? a : b
#define Max(a, b) a > b ? a : b
struct t
{
int min, max;
}map[maxn][ 20 ];
void build ( int n)
{
int i, j, m, r = n, c = log(( double )n) / log( 2.0 );
for (i = 1 ; i <= c; i ++ )
{
for (j = 1 ; j <= r; j ++ )
{
m = j + ( 1 << (i - 1 )); // 鍙沖崐閮ㄥ垎鐨勮搗濮嬪?/span>
if (m <= r)
{
map[j][i].min = Min(map[j][i - 1 ].min ,map[m][i - 1 ].min);
map[j][i].max = Max(map[j][i - 1 ].max, map[m][i - 1 ].max);
}
else // 闀垮害瓚呭嚭n鐨勶紝灝卞綋鏄痡璧風偣鐨勬渶鍚庝竴涓粓鐐圭殑rmq銆傚疄鐜拌繖姝ヨ兘浣挎煡璇負O(1).
{
map[j][i].min = map[j][i - 1 ].min;
map[j][i].max = map[j][i - 1 ].max;
}
}
}
}
int query( int l, int r)
{
int len = r - l + 1 ;
int k = log(( double )len) / log( 2.0 );
int m = r - ( 1 << k) + 1 ;
int min = Min(map[l][k].min, map[m][k].min);
int max = Max(map[l][k].max, map[m][k].max);
return max - min;
}
int main()
{
int n, m, i, l, r;
scanf( " %d%d " , & n, & m);
for (i = 1 ; i <= n; i ++ )
{
scanf( " %d " , & map[i][ 0 ].min);
map[i][ 0 ].max = map[i][ 0 ].min;
}
build (n);
while (m -- )
{
scanf( " %d%d " , & l, & r);
printf( " %d\n " , query(l, r));
}
return 0 ;
}
]]>