Problem Description
General
Gee is the commander of a military base. He has just received alarming
news from one of his spies: the enemy's preparing an air missile strike.
The base contains two magnetic towers. When activated and given
sufficient power, each of the magnetic towers creates a powerful
horizontal magnetic disk. If any missile passes through this disk it
deflects away from the base.
Although those towers seem to be an excellent air defense method, there is a problem: The area of the disk generated by a tower is proportional to the amount of energy it receives. The base has enough power plants to generate a certain amount of energy, which has to be divided among those two towers. That means that the total area of the two disks generated from the towers should not exceed the total energy generated by the power plants. Fortunately, the spy was able to know the exact target co-ordinates of the incoming missiles and he reported them to General Gee. The General needs your help in distributing the energy on the two magnetic towers to minimize the number of missiles that will not get deflected by the magnetic towers and therefore will hit the base. You may assume the following:
1. The towers have different heights and therefore there are no problems associated with the magnetic disks interfering with each other.
2. A missile will deflect if it passes through the magnetic disk of a tower or even if it just touches its boundary.
3. A missile hitting a tower (landing exactly on its location) will deflect, even if the tower is not given any energy.
4. All incoming missiles will go down simultaneously at the exact instant; therefore, there will not be any time available to redistribute the energy amongst the two towers during the strike.
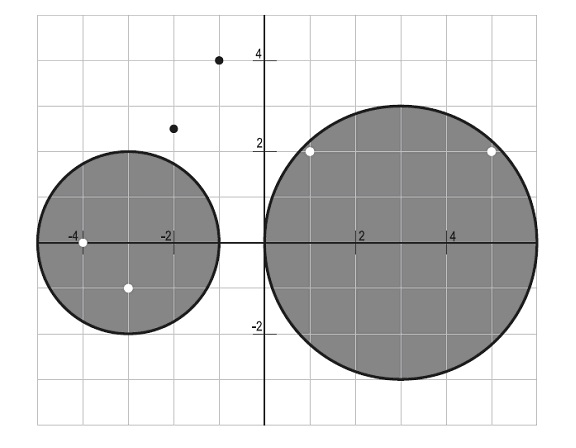
Although those towers seem to be an excellent air defense method, there is a problem: The area of the disk generated by a tower is proportional to the amount of energy it receives. The base has enough power plants to generate a certain amount of energy, which has to be divided among those two towers. That means that the total area of the two disks generated from the towers should not exceed the total energy generated by the power plants. Fortunately, the spy was able to know the exact target co-ordinates of the incoming missiles and he reported them to General Gee. The General needs your help in distributing the energy on the two magnetic towers to minimize the number of missiles that will not get deflected by the magnetic towers and therefore will hit the base. You may assume the following:
1. The towers have different heights and therefore there are no problems associated with the magnetic disks interfering with each other.
2. A missile will deflect if it passes through the magnetic disk of a tower or even if it just touches its boundary.
3. A missile hitting a tower (landing exactly on its location) will deflect, even if the tower is not given any energy.
4. All incoming missiles will go down simultaneously at the exact instant; therefore, there will not be any time available to redistribute the energy amongst the two towers during the strike.
Input
Input consists of several test cases. Each
test case is specified on N+2 lines. The first line contains an integer
(1 <= N <= 1, 000) representing the number of missiles. The second
line contains 5 real numbers X1, Y1, X2,
Y2 and T: (X1, Y1) is the coordinates
of the first tower, (X2, Y2) is the coordinates of
the second tower and (0 <= T) is the total amount of energy
generated from the power plants (the total area of the two magnetic
disks). Each line of the remaining N lines contains two real numbers
representing the landing coordinates of a missile.
The absolute value of all the given real numbers is less than or equal to 100 and may include a decimal point followed by up to 3 digits. Any two consecutive numbers on the same line are separated by one or more white-space characters. Zero or more blank lines may appear between test cases.
The last line of the input file is made of a single zero.
The absolute value of all the given real numbers is less than or equal to 100 and may include a decimal point followed by up to 3 digits. Any two consecutive numbers on the same line are separated by one or more white-space characters. Zero or more blank lines may appear between test cases.
The last line of the input file is made of a single zero.
Output
For each test case, print the following
line:
k. M
Where k is the test case number (starting at one,) and M is the minimum number of missiles that will NOT be deflected in the best distribution of energy among the two towers. Use π = 3.141.
Note: There is a blank space before M.
k. M
Where k is the test case number (starting at one,) and M is the minimum number of missiles that will NOT be deflected in the best distribution of energy among the two towers. Use π = 3.141.
Note: There is a blank space before M.
Sample Input
6
-3 0 3 0 40.833
-1 4
-2 2.5
1 2
5 2
-4 0
-3 -1
2
0 0 1 1 0
0 0
1 1
0
Sample Output
1. 2
2. 0
#include<stdio.h>
#include<stdlib.h>
#define maxn 1000
#define PI 3.141
const double inf = 0.00001;
double d1[maxn], d2[maxn];
double dis(double x1, double y1, double x2, double y2)
{
return 1.0 * (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}
int main()
{
int n, i, j, ans, sum, k = 0;
double r1, r2, r3, r4, r;
double x1, y1, x2, y2, x, y;
while (scanf("%d", &n), n)
{
scanf("%lf%lf%lf%lf%lf", &x1, &y1, &x2, &y2, &r);
r = 1.0 * r / PI;
for (i = 0; i < n; i++)
{
scanf("%lf%lf", &x, &y);
d1[i] = dis(x, y, x1, y1);
d2[i] = dis(x, y, x2, y2);
}
for (i = 0, ans = n; i < n; i++)
{
r1 = d1[i];
if (r1 <= r)//鏋氫婦涓涓偣鍜屽叾涓竴涓鐨勮窛紱籸1,鍒欏墿涓嬬殑紓佹嘗璺濈涓簉2
{
r2 = r - r1;
for (j = 0, sum = 0; j < n; j++)
{
if (d1[j] <= r1)
{
sum++;
}
else if (d2[j] <= r2)
{
sum++;
}
}
if (ans > n - sum)
{
ans = n - sum;
}
}
r2 = d2[i];
if (r2 <= r)
{
r1 = r - r2;
for (j = 0, sum = 0; j < n; j++)
{
if (d1[j] <= r1)
{
sum++;
}
else if (d2[j] <= r2)
{
sum++;
}
}
if (ans > n - sum)
{
ans = n - sum;
}
}
}
k++;
printf("%d. %d\n", k, ans);
}
return 0;
}
]]>
Problem
Description
KERMIT
THE FROG is a classic video game with a simple control and objective
but requires a good deal of thinking.
You control an animated frog that can walk and hop, in both forward and backward directions. The frog stands in a space between an otherwise a contiguous line of tiles. Each tile is painted black on one side, and white on the other. The frog can walk (forward, or backward) over an adjacent tile (in front or behind him.)
When the frog walks over a tile, the tile slides to the space where the frog was standing. For example, in the adjacent figure, the frog has two tiles behind him, and three in front. We’ll use the notation BWFBBW to refer to this situation where F refers to the space (where the frog is standing,) B is a tile with its black face showing, while W is a tile with its white face showing. The forward direction is from left to right. If the frog were to walk forward, the resulting situation is BWBFBW. Similar behavior when the frog walks backward, the tile behind the frog slides to where the frog was standing. The frog can also hop over the tiles. The frog can hop over an adjacent tile landing on the tile next to it. For example, if the frog was to hop backward, it would land on the first (left-most) tile, and the tile would jump to the space where the frog was standing. In addition, the tile would flip sides. For example, hopping backward in the figure would result in the situation: FWWBBW. We challenge you to write a program to determine the minimum number of moves (walks or hops) to transform one tile configuration into another.
You control an animated frog that can walk and hop, in both forward and backward directions. The frog stands in a space between an otherwise a contiguous line of tiles. Each tile is painted black on one side, and white on the other. The frog can walk (forward, or backward) over an adjacent tile (in front or behind him.)
When the frog walks over a tile, the tile slides to the space where the frog was standing. For example, in the adjacent figure, the frog has two tiles behind him, and three in front. We’ll use the notation BWFBBW to refer to this situation where F refers to the space (where the frog is standing,) B is a tile with its black face showing, while W is a tile with its white face showing. The forward direction is from left to right. If the frog were to walk forward, the resulting situation is BWBFBW. Similar behavior when the frog walks backward, the tile behind the frog slides to where the frog was standing. The frog can also hop over the tiles. The frog can hop over an adjacent tile landing on the tile next to it. For example, if the frog was to hop backward, it would land on the first (left-most) tile, and the tile would jump to the space where the frog was standing. In addition, the tile would flip sides. For example, hopping backward in the figure would result in the situation: FWWBBW. We challenge you to write a program to determine the minimum number of moves (walks or hops) to transform one tile configuration into another.
Input
Your program
will be tested on one or more
test cases. Each test case is specified on a single line that specifies
string S representing the initial tile arrangement. S is a non-empty
string and no longer than 100 characters and is made of the letters ’B’,
’W’, and exactly one ’F’. The last line of the input file has one or
more ’-’ (minus) characters.
Output
For each test
case, print the following line:
k. M
Where k is the test case number (starting at one,) and M is the minimum number of moves needed to transform the given arrangement to an arrangement that has no white tile(s) between any of its black tiles . The frog can be anywhere. M is -1 if the problem cannot be solved in less than 10 moves.
Note: There is a blank space before M.
k. M
Where k is the test case number (starting at one,) and M is the minimum number of moves needed to transform the given arrangement to an arrangement that has no white tile(s) between any of its black tiles . The frog can be anywhere. M is -1 if the problem cannot be solved in less than 10 moves.
Note: There is a blank space before M.
Sample
Input
WWBBFBW
WWFBWBW
FWBBWBW
---
Sample
Output
1. 0
2. 1
3. 2
棰樻剰錛氶潚铔欏彲鍚戝墠鎴栧悜鍚庤蛋涓姝ワ紝璧板悗錛岄潚铔欐墍鍦ㄤ綅緗殑鐮栨粦鍒伴潚铔欐病璺沖墠鐨勪綅緗傞潚铔欎篃鍙互鍚戝墠璺蟲垨鍚戝悗璺籌紝璺充竴嬈¤兘璺寵繃2涓爾錛?br>闈掕洐鎵鍦ㄤ綅緗殑鐮栫炕杞悗婊戝埌闈掕洐娌¤煩鍓嶇殑浣嶇疆銆傛眰闈掕洐鍦ㄥ崄涓姩浣滀箣鍐咃紝浣夸換鎰忎袱涓粦鐮栦箣闂存病鐧界爾鐨勬渶灝忔鏁般?br>
#include<stdio.h>
#include<string.h>
#define maxn 300000
int ans, len;
char state[maxn][100];
char step[maxn], f[maxn];
int check(int depth)
{
int i, j, x, y;
for (i = 0, j = len - 1, x = y = -1; i < len; i++, j--)
{
if (state[depth][i] == 'B' && x == -1)
{
x = i;
}
if (state[depth][j] == 'B' && y == -1)
{
y = j;
}
}
if (x != -1 && y != -1)
{
for (i = x + 1; i < y; i++)
{
if (state[depth][i] == 'W')
{
return 0;
}
}
}
return 1;
}
void swap(int depth, int i, int j)
{
state[depth][i] ^= state[depth][j];
state[depth][j] ^= state[depth][i];
state[depth][i] ^= state[depth][j];
}
void hopf(int depth, int i)
{
swap(depth, i, i + 2);
state[depth][i] = (state[depth][i] == 'B') ? 'W' : 'B' ;
}
void hopb(int depth, int i)
{
swap(depth, i, i - 2);
state[depth][i] = (state[depth][i] == 'B') ? 'W' : 'B' ;
}
void bfs()
{
int head = 0, tial = 1, h;
if (check(0))
{
ans = 0;
return;
}
while (head < tial)
{
if (step[head] >= 9)
{
return;
}
h = f[head];
if (h + 1 < len)
{
strcpy(state[tial], state[head]);
swap(tial, h, h + 1);
step[tial] = step[head] + 1;
f[tial] = h + 1;
if (check(tial))
{
ans = step[tial];
return;
}
tial++;
}
if (h - 1 >= 0)
{
strcpy(state[tial], state[head]);
swap(tial, h, h - 1);
step[tial] = step[head] + 1;
f[tial] = h - 1;
if (check(tial))
{
ans = step[tial];
return;
}
tial++;
}
if (h + 2 < len)
{
strcpy(state[tial], state[head]);
hopf(tial, h);
step[tial] = step[head] + 1;
f[tial] = h + 2;
if (check(tial))
{
ans = step[tial];
return;
}
tial++;
}
if (h - 2 >= 0)
{
strcpy(state[tial], state[head]);
hopb(tial, h);
step[tial] = step[head] + 1;
f[tial] = h - 2;
if (check(tial))
{
ans = step[tial];
return;
}
tial++;
}
head++;
}
}
int main()
{
int i, j, k = 0;
char s[100];
while (scanf("%s", s), s[0] != '-')
{
k++;
ans = 10;
for (i = 0; (state[0][i] = s[i]) != 0; i++)
{
if (s[i] == 'F')
{
j = i;
}
}
len = i;
strcpy(state[0], s);
step[0] = 0;
f[0] = j;
bfs();
printf("%d. %d\n", k, ans < 10 ? ans : -1);
}
}
]]>